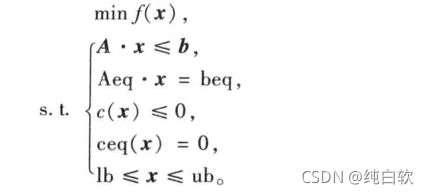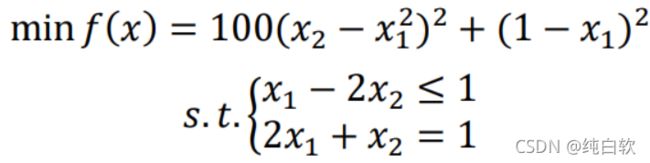第三天打卡--非线性规划(1)
练习matlab的第三天
目录
一、非线性规划
二、题目
Ⅰ、线性约束条件
1、写出目标函数f(x)
2、代码实现
Ⅱ、非线性约束条件
1、写出目标函数f(x)
2、写出约束条件c(x),ceq(x)
3、代码实现
Ⅲ、特别的
三、练习
四、思考
一、非线性规划
非线性规划分有很多种类,比如有约束的非线性规划、无约束的非线性规划等。特殊的有二次规划等。今天学习有约束的非线性规划。
Matlab中非线性规划的数学模型为:
而Matlab中的命令是
x = fmincon(fun,x0,A,b)
x = fmincon(fun,x0,A,b,Aeq,beq)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)分析
①fun为所求的目标函数![]() 。
。
②x0为fun函数中变量x的起始值。
③nonlcon为非线性的不等式约束函数![]() 与等式约束函数
与等式约束函数![]() 。
。
④options为所定义的优化参数,也可以直接使用Matlab的默认参数。
⑤A,b,Aeq,beq均为线性约束条件,当其不存在的时候可以用[ ]代替。
二、题目
Ⅰ、线性约束条件
1、写出目标函数f(x)
fun = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;%这里使用匿名函数
2、代码实现
clc;
clear;
x0 = [0,0];
A = [1,-2];
b = 1;
Aeq = [2,1];
beq = 1;
[x,fval] = fmincon(fun,x0,A,b,Aeq,beq)
运行结果:
Ⅱ、非线性约束条件
目标函数:
![]()
约束条件:
![]()
![]()
![]()
![]()
![]()
1、写出目标函数f(x)
function f=fun(x)
f=sum(x.^2)+8;
end2、写出约束条件c(x),ceq(x)
function [c,ceq]=nonlcon(x)
c=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^3-20]; %非线性不等式约束
ceq=[-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3]; %非线性等式约束
end
3、代码实现
clear;
clc;
fun=x(1)^2+x(2)^2+x(3)^2+8;
function f=fun(x)
f=sum(x.^2)+8;
end
function [c,ceq]=nonlcon(x)
c=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^3-20]; %非线性不等式约束
ceq=[-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3]; %非线性等式约束
end
options=optimset('largescale','off');
[x,fval] = fmincon(@fun,rand(3,1),[],[],[],[],zeros(3,1),[], @nonlcon, options);解释:
①options=optimset('largescale','off');这是对寻优函数搜索方式的设定,LargeScale指大规模搜索,off表示在规模搜索模式关闭。
②rand(3,1)指x1,x2,x3均以0~1的随机数为起始值。
Ⅲ、特别的
代码中使用了匿名函数@fun。
当不使用匿名函数时,就必须将fun函数与c(x)和ceq(x)分别写在一个文件里,并且函数fmincon使用方式也会改变,如下:
文件fun.m
function f=fun(x)
f=sum(x.^2)+8;
end
文件nonlcon.m
function [c,ceq]=nonlcon(x)
c=[-x(1)^2+x(2)-x(3)^2
x(1)+x(2)^2+x(3)^3-20]; %非线性不等式约束
ceq=[-x(1)-x(2)^2+2
x(2)+2*x(3)^2-3]; %非线性等式约束
end
[x,favl] = fmincon('fun',rand(3,1),[],[],[],[],zeros(3,1),[], 'nonlcon', options)
三、练习
代码实现:
clc;
clear;
a=[-1 -2 0;-1 0 0];
b=[-1;0];
[x,y]=fmincon(@fun,rand(3,1),a,b,[],[],[],[],@nonlcon);
x'
y=-y
function y=fun(x)
c1=[2 3 1];
c2=[3 1 0];
y=c1*x+c2*x.^2;
y=-y;
end
function [f,g]=nonlcon(x)
f=[x(1)+2*x(1)^2+x(2)+2*x(2)^2+x(3)-10
x(1)+x(1)^2+x(2)+x(2)^2-x(3)-50
2*x(1)+x(1)^2+2*x(2)+x(3)-40];
g=x(1)^2+x(3)-2;
end
运行结果:
四、思考
①典型的模型翻译,主要重点是根据题目条件编写目标函数f(x)。
②与线性规划相同的思路。