Datawhale集成学习学习笔记——机器学习基础

机器学习的三大主要任务

机器学习的一个重要的目标就是利用数学模型来理解数据，发现数据中的规律，用作数据的分析和预测。

数据通常由一组向量组成，这组向量中的每个向量都是一个样本，我们用$x_i$来表示一个样本，其中$i=1,2,3,...,N$,共N个样本，每个样本$x_i=(x_{i1},x_{i2},...,x_{ip},y_i)$共p+1个维度，前p个维度的每个维度我们称为一个特征，最后一个维度$y_i$我们称为因变量(响应变量)。特征用来描述影响因变量的因素。通常在一个数据表dataframe里面，一行表示一个样本$x_i$，一列表示一个特征。

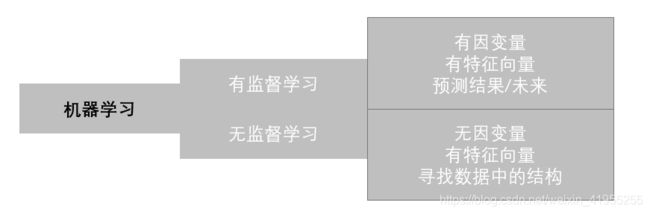
• 根据数据是否有因变量，机器学习的任务可分为：

  

  • 有监督学习：给定某些特征去估计因变量，即因变量存在的时候，我们称这个机器学习任务为有监督学习。如：我们使用房间面积，房屋所在地区，环境等级等因素去预测某个地区的房价。
  • 无监督学习：给定某些特征但不给定因变量，建模的目的是学习数据本身的结构和关系。如：我们给定某电商用户的基本信息和消费记录，通过观察数据中的哪些类型的用户彼此间的行为和属性类似，形成一个客群。注意，我们本身并不知道哪个用户属于哪个客群，即没有给定因变量。

• 根据因变量的是否连续，有监督学习又分为

  • 回归: 连续变量
  • 分类: 离散变量

为了更好地叙述后面的内容，我们对数据的形式作出如下约定：

• 第i个样本：$x_i=(x_{i1},x_{i2},...,x_{ip},y_i{)}^T,i=1,2,...,N$

• 因变量: $y=(y_1,y_2,...,y_N{)}^T$

• 第k个特征: $x^{(k)}=(x_{1k},x_{2k},...,x_{Nk}{)}^T$

• 特征矩阵: $X=(x_1,x_2,...,x_N{)}^T$

• 例子

  • 回归: Boston房价数据集

    from sklearn import datasets
    boston = datasets.load_boston()
    X = boston.data
    y = boston.target
    features = boston.feature_names
    

  • 分类: iris鸢尾花数据集

    from sklearn import datasets
    iris = datasets.load_iris()
    X = iris.data
    y = iris.target
    features = iris.feature_names
    

  • 无监督学习

    • https://scikit-learn.org/stable/modules/classes.html?highlight=datasets#module-sklearn.datasets

使用sklearn构建完整的机器学习项目流程

• 步骤
  • 明确项目任务：回归/分类
  • 收集数据集并选择合适的特征。
  • 选择度量模型性能的指标。
  • 选择具体的模型并进行训练以优化模型。
  • 评估模型的性能并调参

基本的回归模型

• 选择度量模型性能的指标。
  • Sklearn函数
  • MSE均方误差：$\text{MSE}(y,\hat{y})=\frac{1}{n_{\text{samples}}}{\sum }_{i=0}^{n_{\text{samples}}-1}(y_i-{\hat{y}}_i{)}^2$
  • MAE平均绝对误差:$\text{MAE}(y,\hat{y})=\frac{1}{n_{\text{samples}}}{\sum }_{i=0}^{n_{\text{samples}}-1}\left|y_i-{\hat{y}}_i\right|$
  • $R^2$决定系数：$R^2(y,\hat{y})=1-\frac{{\sum }_{i=1}^n(y_i-\hat{y}i{)}^2}{\sum {i=1}^n(y_i-\bar{y}{)}^2}$
  • 解释方差得分: $explained\_variance(y,\hat{y})=1-\frac{Var\{y-\hat{y}\}}{Var\{y\}}$
• 选择具体的模型并进行训练以优化模型。
  • 线性回归模型
    • 最小二乘估计
    • 几何解释
    • 概率视角
    • 推广
      • 多项式回归
      • 广义可加模型(GAM)
  • 回归树
  • 支持向量机回归(SVR)

基本的分类模型

• 选择度量模型性能的指标。
  

  • Sklearn函数
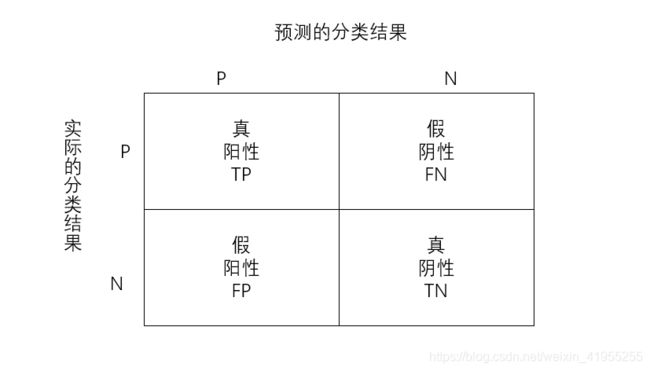
  • 准确率：分类正确的样本数占总样本的比例，即：$ACC=\frac{TP+TN}{FP+FN+TP+TN}$.
  • 精度：预测为正且分类正确的样本占预测值为正的比例，即：$PRE=\frac{TP}{TP+FP}$.
  • 召回率：预测为正且分类正确的样本占类别为正的比例，即：$REC=\frac{TP}{TP+FN}$.
  • F1值：综合衡量精度和召回率，即：$F1=2\frac{PRE\times REC}{PRE+REC}$.
  • ROC曲线：以假阳率为横轴，真阳率为纵轴画出来的曲线，曲线下方面积越大越好。

• 选择具体的模型并进行训练以优化模型。

  • 逻辑回归
  • 基于概率的分类模型
    • 线性判别分析
    • 朴素贝叶斯
  • 决策树
  • 支持向量机SVM
  • 非线性支持向量机

偏差与方差理论

• 训练均方误差与测试均方误差: 一个模型的训练均方误差最小时, 不能保证测试均方误差同时很小

• 偏差-方差的权衡

  $$E{\left(y_0-\hat{f}\left(x_0\right)\right)}^2=\mathrm{Var}\left(\hat{f}\left(x_0\right)\right)+{\left[\mathrm{Bias}\left(\hat{f}\left(x_0\right)\right)\right]}^2+\mathrm{Var}(\epsilon )$$

  • 测试均方误差的期望值可以分解为$\hat{f}(x_0)$的方差、$\hat{f}(x_0)$的偏差平方和误差项$ϵ$的方差
  • 建模任务的难度(不可约误差): $\mathrm{Var}(\epsilon )$, 任务确定后无法改变的,
  • 偏差度量的是单个模型的学习能力，而方差度量的是同一个模型在不同数据集上的稳定性。
  • “偏差-方差分解”说明：泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。给定学习任务，为了取得好的泛化性能，则需使偏差较小，即能够充分拟合数据，并且使方差较小，即使得数据扰动产生的影响小。
  • 一般来说, 模型的复杂度越高, 会增加模型的方差，但是会减少模型的偏差

• 特征提取

  • 要选择一个测试误差达到最小的模型。但是实际上我们很难对实际的测试误差做精确的计算，因此要对测试误差进行估计，估计的方式有两种：训练误差修正与交叉验证。
    • 训练误差修正: 对测试误差的间接估计
      • 模型越复杂，训练误差越小，测试误差先减后增
      • 先构造一个特征较多的模型使其过拟合，此时训练误差很小而测试误差很大，那这时加入关于特征个数的惩罚。因此，当我们的训练误差随着特征个数的增加而减少时，惩罚项因为特征数量的增加而增大，抑制了训练误差随着特征个数的增加而无休止地减小。具体的数学量如下$C_p=\frac{1}{N}(RSS+2d{\hat{\sigma }}^2)$，其中d为模型特征个数，$RSS=\sum _{i=1}^N(y_i-\hat{f}(x_i){)}^2$, ${\hat{\sigma }}^2$为模型预测误差的方差的估计值，即残差的方差。
      • AIC赤池信息量准则：$AIC=\frac{1}{d{\hat{\sigma }}^2}(RSS+2d{\hat{\sigma }}^2)$
      • BIC贝叶斯信息量准则：$BIC=\frac{1}{n}(RSS+log(n)d{\hat{\sigma }}^2)$
      • 这种方法的桥梁是训练误差
    • 交叉验证: 对测试误差的直接估计
      • 交叉验证比训练误差修正的优势在于：能够给出测试误差的一个直接估计
      • K折交叉验证得到的测试误差估计: $C{V}_{(K)}=\frac{1}{K}{\sum }_{i=1}^{K}MS{E}_i$
  • 在测试误差能够被合理的估计出来以后，我们做特征选择的目标就是：从p个特征中选择m个特征，使得对应的模型的测试误差的估计最小

    • 最优子集选择

      1. 记不含任何特征的模型为$M_0$，计算这个$M_0$的测试误差。
      2. 在$M_0$基础上增加一个变量，计算p个模型的RSS，选择RSS最小的模型记作$M_1$，并计算该模型$M_1$的测试误差。
      3. 再增加变量，计算p-1个模型的RSS，并选择RSS最小的模型记作$M_2$，并计算该模型$M_2$的测试误差。
      4. 重复以上过程知道拟合的模型有p个特征为止，并选择p+1个模型$\{M_0,M_1,...,M_p\}$中测试误差最小的模型作为最优模型。

    • 向前逐步选择

      • 最优子集选择虽然在原理上很直观，但是随着数据特征维度p的增加，子集的数量为$2^p$，计算效率非常低下且需要的计算内存也很高，在大数据的背景下显然不适用。因此，我们需要把最优子集选择的运算效率提高，因此向前逐步选择算法的过程如下：
      1. 记不含任何特征的模型为$M_0$，计算这个$M_0$的测试误差。
      2. 在$M_0$基础上增加一个变量，计算p个模型的RSS，选择RSS最小的模型记作$M_1$，并计算该模型$M_1$的测试误差。
      3. 在最小的RSS模型下继续增加一个变量，选择RSS最小的模型记作$M_2$，并计算该模型$M_2$的测试误差。
      4. 以此类推，重复以上过程知道拟合的模型有p个特征为止，并选择p+1个模型$\{M_0,M_1,...,M_p\}$中测试误差最小的模型作为最优模型。

      #定义向前逐步回归函数
      def forward_select(data,target):
          variate=set(data.columns)  #将字段名转换成字典类型
          variate.remove(target)  #去掉因变量的字段名
          selected=[]
          current_score,best_new_score=float('inf'),float('inf')  #目前的分数和最好分数初始值都为无穷大（因为AIC越小越好）
          #循环筛选变量
          while variate:
              aic_with_variate=[]
              for candidate in variate:  #逐个遍历自变量
                  formula="{}~{}".format(target,"+".join(selected+[candidate]))  #将自变量名连接起来
                  aic=ols(formula=formula,data=data).fit().aic  #利用ols训练模型得出aic值
                  aic_with_variate.append((aic,candidate))  #将第每一次的aic值放进空列表
              aic_with_variate.sort(reverse=True)  #降序排序aic值
              best_new_score,best_candidate=aic_with_variate.pop()  #最好的aic值等于删除列表的最后一个值，以及最好的自变量等于列表最后一个自变量
              if current_score>best_new_score:  #如果目前的aic值大于最好的aic值
                  variate.remove(best_candidate)  #移除加进来的变量名，即第二次循环时，不考虑此自变量了
                  selected.append(best_candidate)  #将此自变量作为加进模型中的自变量
                  current_score=best_new_score  #最新的分数等于最好的分数
                  print("aic is {},continuing!".format(current_score))  #输出最小的aic值
              else:
                  print("for selection over!")
                  break
          formula="{}~{}".format(target,"+".join(selected))  #最终的模型式子
          print("final formula is {}".format(formula))
          model=ols(formula=formula,data=data).fit()
          return(model)
      

• 压缩估计(正则化)

  除了直接对特征自身进行选择以外，还可以对回归的系数进行约束或者加罚的技巧对p个特征的模型进行拟合，显著降低模型方差，这样也会提高模型的拟合效果。具体来说，就是将回归系数往零的方向压缩.

  • 岭回归(L2正则化的例子)

    $$\begin{gathered} J(w)=\sum _{i=1}^N(y_i-w_0-\sum _{j=1}^p{w}_j{x}_{ij}{)}^2+\lambda \sum _{j=1}^p{w}_j^2,其中，\lambda \ge 0 \\ \hat{w}=(X^{T}X+\lambda I{)}^{-1}{X}^{T}Y \end{gathered}$$

    调节参数$\lambda$的大小是影响压缩估计的关键，$\lambda$越大，惩罚的力度越大，系数则越趋近于0，反之，选择合适的$\lambda$对模型精度来说十分重要。岭回归通过牺牲线性回归的无偏性降低方差，有可能使得模型整体的测试误差较小，提高模型的泛化能力。

    将模型的系数往零的方向压缩，但是岭回归的系数只能呢个趋于0但无法等于0，换句话说，就是无法做特征选择

  • Lasso回归(L1正则化的例子)

    $$J(w)=\sum _{i=1}^N(y_i-w_0-\sum _{j=1}^p{w}_j{x}_{ij}{)}^2+\lambda \sum _{j=1}^p|w_j|,其中，\lambda \ge 0$$

    • 特征选择

  • 区别:

    

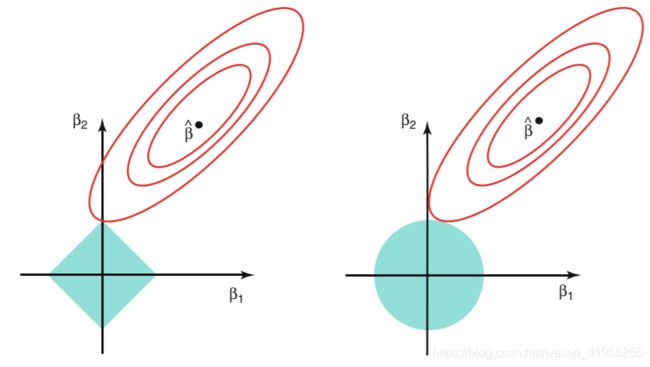
    • 椭圆形曲线为RSS等高线，菱形和圆形区域分别代表了L1和L2约束，Lsaao回归和岭回归都是在约束下的回归，因此最优的参数为椭圆形曲线与菱形和圆形区域相切的点。但是Lasso回归的约束在每个坐标轴上都有拐角，因此当RSS曲线与坐标轴相交时恰好回归系数中的某一个为0，这样就实现了特征提取。反观岭回归的约束是一个圆域，没有尖点，因此与RSS曲线相交的地方一般不会出现在坐标轴上，因此无法让某个特征的系数为0，因此无法做到特征提取。

• 降维

  • 降维的本质是学习一个映射函数 f : x->y，其中x是原始数据点的表达，目前最多使用向量表达形式。 y是数据点映射后的低维向量表达，通常y的维度小于x的维度
  • f可能是显式的或隐式的、线性的或非线性的。
  • 在很多算法中，降维算法成为了数据预处理的一部分，如PCA。事实上，有一些算法如果没有降维预处理，其实是很难得到很好的效果的。
  • 主成分分析(PCA): 通过最大投影方差 将原始空间进行重构，即由特征相关重构为无关，即落在某个方向上的点(投影)的方差最大。

超参数调优

• 超参数: 无法使用最优化算法优化出来的数
  • 模型参数是模型内部的配置变量，其值可以根据数据进行估计。
    • 进行预测时需要参数。
    • 它参数定义了可使用的模型。
    • 参数是从数据估计或获悉的。
    • 参数通常不由编程者手动设置。
    • 参数通常被保存为学习模型的一部分。
    • 参数是机器学习算法的关键，它们通常由过去的训练数据中总结得出 。
  • 模型超参数是模型外部的配置，其值无法从数据中估计。
    • 超参数通常用于帮助估计模型参数。
    • 超参数通常由人工指定。
    • 超参数通常可以使用启发式设置。
    • 超参数经常被调整为给定的预测建模问题。
• 调优方法
  • 网格搜索GridSearchCV()
  • 随即搜索RandomizedSearchCV()