pytorch中张量对张量的梯度求解:backward方法的gradient参数详解

一、问题起源：
阅读《python深度学习：基于pytorch》这本书的tensor 与Autograd一节时，看到2.5.4非标量反向传播

二、疑点在于：

backward(gradient=)这一参数没有理由的就选择了(1,1)，之后调整为(1,0)和(0,1)便能正确求解，对该参数的设置原理，反向梯度求解的过程没有说清楚。

三、分析过程：

看完博客https://www.cnblogs.com/zhouyang209117/p/11023160.html 

便确认gradient这一参数的设置应该是根据使用者的需求，比如说设置为(1,0)就正好求得y1对x的导数。

但是两者的求解过程不一致，书中=J的转置*V的转置，但是博客中假设的是V*J ，其实解释的原理都是一样的 ，就是希望设置V来分别在y的不同分量上求得对x的导数，然后组合向量，获得最终y对于x的导数。

虽然求解过程，但各偏导值是一致的。

书中x.grad = [[6,9]],但是博客中只有x1,x2,x3的梯度值，即便将代码改为对x求导，结果x.grad=None

x = torch.tensor([1,2,3],requires_grad=True, dtype=torch.float)

y.backward(torch.tensor([1, 1, 1], dtype=torch.float))

print(x.grad)  # None  因为y赋值的时候是通过x1,x2,x3标量赋值的 ，与x无关。

 

如果改成以下代码：

 

y[0] = x[0]*x[1]*x[2]

y[1] = x[0]+x[1]+x[2]

y[2] = x[0]+x[1]*x[2]

y.backward(torch.tensor([1, 1, 1], dtype=torch.float))

print(x.grad) #tensor([8., 7., 5.])

则结果为tensor([8., 7., 5.]),梯度值shape为(1,3)，与初始值x的shape保持一致

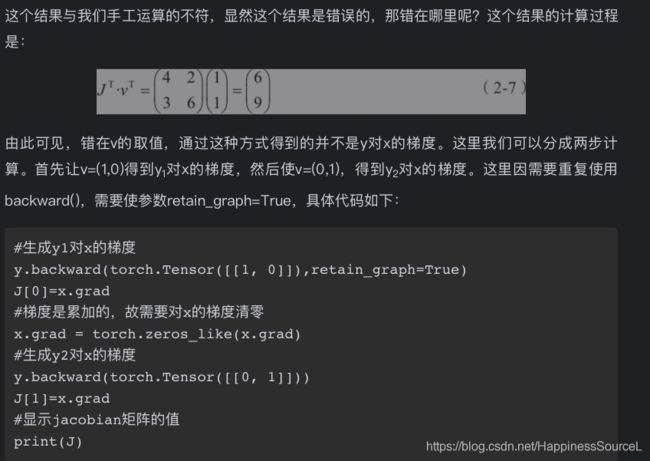
书中虽然计算过程为J的转置*V的转置，结果为列向量(6,9)，但是输出值是[[6,9]]，为行向量。 所以经过验证可知，实际的计算过程是gradient*Jacobian 。

另外check了官网的doc描述如下：其实对参数grad_tensors的描述并不是很清晰的，只提到了jacobian-voector product。如果有get到了这段话描述的具体计算过程的，或者与我理解的有不符合的 欢迎交流。就没有去check源代码了，因为两个测试代码段的计算结果和我以及上述博客的grad_tensors*jacobian是一致的。

书中原始代码块如下：

博客代码块如下，这个对A的假设是很好地，但是我们实际求的还是y对于x的偏导数，所以要构造A对y的偏导矩阵v与y对于x的偏导矩阵J 来做点积，这样实际求得的分量就是y对于x的偏导数：

# coding utf-8
import torch

x1 = torch.tensor(1, requires_grad=True, dtype=torch.float)
x2 = torch.tensor(2, requires_grad=True, dtype=torch.float)
x3 = torch.tensor(3, requires_grad=True, dtype=torch.float)
y = torch.randn(3)
y[0] = x1 * x2 * x3
y[1] = x1 + x2 + x3
y[2] = x1 + x2 * x3
x = torch.tensor([x1, x2, x3])
y.backward(torch.tensor([0.1, 0.2, 0.3], dtype=torch.float))
print(x1.grad)
print(x2.grad)
print(x3.grad)

我的测试代码块如下:

# coding utf-8
import torch

#x1 = torch.tensor(1, requires_grad=True, dtype=torch.float)
#x2 = torch.tensor(2, requires_grad=True, dtype=torch.float)
#x3 = torch.tensor(3, requires_grad=True, dtype=torch.float)
x = torch.tensor([1,2,3],requires_grad=True, dtype=torch.float)

y = torch.randn(3)
#y[0] = x1 * x2 * x3
#y[1] = x1 + x2 + x3
#y[2] = x1 + x2 * x3
#x = torch.tensor([x1, x2, x3],requires_grad=True)

y[0] = x[0]*x[1]*x[2]
y[1] = x[0]+x[1]+x[2]
y[2] = x[0]+x[1]*x[2]
y.backward(torch.tensor([1, 1, 1], dtype=torch.float)) #只能对float类型求梯度
#print(x1.grad)
#print(x2.grad)
#print(x3.grad)
print(x.grad)  #tensor([8., 7., 5.])

x = torch.tensor([[2,3]])
print(x.shape) #torch.Size([1, 2])