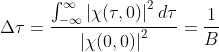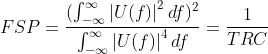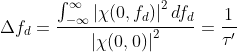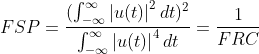Shen_KL
Shen_KL

雷达信号处理---雷达分辨率

雷达的分辨率是指在各种各样的环境下将将两个或两个以上的物体区别开来的能力。一般从四个方面进行区分-------距离、方位、速度、仰角。距离的分辨率取决于信号带宽，方位和仰角的分辨率取决与波束宽度。在实际环境中，只要以上四维中任意一维能区分目标，就认为具有目标分辨的能力。这里主要分析距离分辨率和速度分辨率。 

关键词：时延分辨率\Delta \tau,距离分辨率\Delta R,时延分辨常数TRC,频谱持续宽度FSP,距离分辨常数C_{R},多普勒分辨率\Delta f_{d},速度分辨率\Delta v,频率分辨常数FRC,时间持续宽度(有效相关时间)TSP,速度分辨常数C_{v}

距离分辨率

假定两个目标在同一角度保持同一速度但处在不同距离时，可以用距离模糊函数来衡量分辨能力，见下式

\left | \chi \left ( \tau ,0 \right ) \right |=\left | \int_{-\infty }^{\infty } u(t)u^{*}(t+\tau )dt\right |

根据上一篇博客中的讲述，距离模糊函数\left | \chi (\tau ,0)) \right |随着\tau的增大下降的越快，说明分辨能力越强。

（因为下降的快意味着信号的主瓣尖锐，能量集中，对于两个时延小的目标有很好的分辨能力）

我们一般用距离模糊函数的主瓣宽度(通常取3dB带宽，但是遇到sinc函数时会取4dB带宽，因为sinc函数的4dB带宽是常数，方便计算)来定义固有分辨率，称为名义距离分辨率，简称距离分辨率\tau _{nr}。

在这里我们先引入时延分辨率，其定义式为

\Delta \tau =\frac{\int_{-\infty }^{\infty }\left | \chi (\tau ,0)\right |^{2} d\tau }{\left | \chi (0,0) \right |^{2}}=\frac{1}{B}

其中B为有效带宽，该定义式的含义在下文中有解释。而时延分辨率所对应的距离分辨率为

\Delta R=\frac{c\Delta \tau }{2}=\frac{c}{2B}

可见，信号带宽越宽，脉冲宽度越窄，距离分辨率越高。

但是在实际环境中，我们需要全面考虑主瓣和旁瓣的分辨问题，因此定义时延分辨常数TRC来反映分辨特性，其表达式为

TRC=\frac{\int_{-\infty }^{\infty }\left | \chi (\tau ,0)\right |^{2} d\tau }{\left | \chi (0,0) \right |^{2}}=\frac{\int_{-\infty }^{\infty }\left | U(f) \right |^{4}df}{(\int_{-\infty }^{\infty }\left | U(f) \right |^{2}df)^{2}}

时延分辨常数是将主瓣、旁瓣或类似噪声的基地型旁瓣的能量全部相加再除以主板峰值的功率大小。可见，该常数越小，说明主瓣能量越集中，其宽度越窄，分辨能力越强。

在引入一个反映分辨特性的参数------频谱持续宽度FSP（或称有效相关带宽）。其反映的是模糊函数与冲激函数的相似程度（与冲激函数越相似，分辨能力越好）。其表达式为

FSP=\frac{(\int_{-\infty }^{\infty }\left | U(f) \right |^{2}df)^{2}}{\int_{-\infty }^{\infty }\left | U(f) \right |^{4}df}=\frac{1}{TRC}

因此距离分辨常数C_{R}可以表示为

C_{R}=\frac{c\cdot TRC}{2}=\frac{c}{2\cdot FSP}

由上式不难看出，时延分辨常数TRC越小，或频谱持续宽度FSP越宽，距离分辨率越好。因此，信号只要具有大的持续宽度就能获得高的距离分辨力，而不必具有很窄的脉冲宽度。（注意将时延分辨率\Delta \tau与脉冲宽度\tau区分开来，\Delta \tau与带宽B有关）

速度分辨率

信号的速度分辨率由速度模糊函数决定

\left | \chi (0,f_{d}) \right |=\int_{-\infty }^{\infty }\left | u(t) \right |^{2}e^{j2\pi f_{d}t}dt

多普勒分辨率\Delta f_{d}为

\Delta f_{d} =\frac{\int_{-\infty }^{\infty }\left | \chi (0 ,f_{d})\right |^{2} df_{d}}{\left | \chi (0,0) \right |^{2}}=\frac{1}{\tau'}

其中，\tau '是脉冲宽度。而相应的速度分辨率\Delta v为

\Delta v=\frac{c\Delta f_{d}}{2f_{0}}=\frac{\lambda }{2\tau '}

同样，在速度分辨率中，我们同样定义了两个用来表征速度分辨率大小的常数---频率分辨常数FRC和时间持续宽度(有效相关时间)TSP

 FRC=\frac{\int_{-\infty }^{\infty }\left | \chi (0 ,f_{d})\right |^{2} d\tau }{\left | \chi (0,0) \right |^{2}}=\frac{\int_{-\infty }^{\infty }\left | u(t)\right |^{4}dt}{(\int_{-\infty }^{\infty }\left | u(t) \right |^{2}dt)^{2}}

FSP=\frac{(\int_{-\infty }^{\infty }\left | u(t) \right |^{2}dt)^{2}}{\int_{-\infty }^{\infty }\left | u(t) \right |^{4}dt}=\frac{1}{FRC}

由上式可得表征速度分辨率的速度分辨常数为

C_{v}=\frac{c\cdot FRC}{2f_{0}}=\frac{\lambda }{2\cdot TSP}

可见，频率分辨常数FRC越小或者时间持续宽度(有效相关时间)TSP越大，速度分辨率越好。

结论

距离分辨率取决于信号的频率结构，为了提高距离分辨率，信号就需要有大的带宽；而速度分辨率取决于信号的时间结构，为了提高速度分辨率，信号就需要有大的时宽。

但是，根据雷达模糊原理可知，我们无法在不断提高的距离分辨率的同时，提高速度分辨率，其中一种分辨率的提高必然会导致另一种分辨率的衰减。我们用时宽带宽积，即时宽与带宽的乘积(TB)表示信号的距离分辨率与速度分辨率的关系。对于系统设计而言，时宽带宽积越大越好，这意味着我们在提高距离分辨率的同时，不会影响速度分辨率。

如何使得时宽带宽积增大，就涉及到脉内非线性相位调制技术。

你可能感兴趣的:(信号处理,数字信号处理)

  • DSP和ARM的优劣比较（也有FPGA） bingfeng_adonis 工作
    概念1.FPGA:是可编程逻辑阵列，常用于处理高速数字信号，不过随着科技的发展，现在很多FPGACPLD可以集成mcu内核，甚至具备了ARMDSP的功能2.ARM,是一类内核的称谓，就像51一样，具体到芯片的话，会有很多不同的厂家不同等级，诸如三星、易法、飞利浦、摩托罗拉等等，其中STM32是易法半导体的一款面向工控低功耗内核为CortexM3内核的ARM芯片3.DSP顾名思义就是数字信号处理，厂
  • 麒麟SoC的详细架构组成介绍 小蘑菇二号 麒麟
    目录麒麟SoC的主要组成部分1.应用处理器（ApplicationProcessor,AP）2.图形处理单元（GPU）3.神经网络处理单元（NPU）4.图像信号处理器（ISP）5.调制解调器（Modem,基带芯片）6.多媒体编解码器7.安全模块8.连接模块9.存储控制器10.电源管理单元（PMIC）典型麒麟SoC示例Kirin9000总结麒麟（Kirin）是华为自主研发的一系列高性能系统级芯片（S
  • 拉普拉斯逆变换 (Inverse Laplace Transform) 正是读书时 知识点信号处理信息与通信
    拉普拉斯逆变换(InverseLaplaceTransform)概述拉普拉斯逆变换是拉普拉斯变换的逆过程，用于将频域中的函数转换回时域。拉普拉斯变换在信号处理、控制理论和系统分析中具有广泛的应用，而拉普拉斯逆变换则用于将分析得到的结果转换回时域，以便理解和应用实际的系统行为。定义(以单边s变换举例)设\(F(s)\)是一个复变量\(s\)的函数，且\(F(s)\)是某个时域函数\(f(t)\)的拉
  • simulink介绍-ChatGPT4o作答 部分分式 matlab
    Simulink是MATLAB的一个附加模块，由MathWorks开发，用于多领域的动态系统建模、仿真和分析。它提供了基于图形化的拖放式界面，让用户可以通过图形化的方式构建复杂的系统模型，从而进行控制系统、信号处理、通信系统、自动控制等应用领域的设计和仿真。以下是Simulink的详细介绍：1.Simulink的核心功能Simulink的主要功能包括：图形化建模：Simulink提供直观的图形化界
  • 欧拉公式在信号处理中的魔法：调幅信号的生成与频谱分析 CSer、子瑜 数理统计信号处理人工智能
    欧拉公式在信号处理中的魔法：调幅信号的生成与频谱分析“数学不是枯燥的符号，而是宇宙的诗歌。”当我们用欧拉公式解开调幅信号的频谱密码时，仿佛看到电磁波在时空中跳动的频率之舞。这篇博客将带你亲手触摸信号处理中的数学之美。一、当欧拉公式遇见调幅信号：一场数学与工程的联姻在通信工程中，**调幅（AM）**技术就像一位忠实的信使，将我们的声音、音乐等低频信号驮载在高频载波上，穿越城市与山海。而这一切的数学基
  • go实战微服务：微服务与RPC中间件 鱼弦 Golang学习与实战golang微服务rpc
    本文将详细介绍Go微服务与RPC中间件的相关内容，包括信号处理、平滑关闭HTTP服务、图片服务器实现、数据验证、RPC简介、net/rpc和jsonrpc实战，以及基于结构体实现的中间件。每个主题将按照初、中、高级逐步展开。Signal使用初级用法：捕获退出信号介绍捕获系统信号以便在程序终止前进行清理工作。代码实现packagemainimport("fmt""os""os/signal""sys
  • 综合振动分析工具箱 不胖的羊
    本文还有配套的精品资源，点击获取简介：振动工具箱是一个集成了多种振动计算与分析功能的软件或代码库，适用于学习和研究振动现象。它包括处理振动问题的算法、模型和实用程序，覆盖了振动基础理论、简谐振动、阻尼振动、非线性振动、振动分析方法、模态分析、信号处理、频谱分析、数值模拟、振动控制和实验测试等知识领域。通过使用这个工具箱，初学者可以通过实践深入理解和掌握振动分析技术，提高在相关领域的专业技能。1.振
  • 【SCI2区】雾凇优化算法RIME-CNN-GRU-Attention用电需求预测Matlab实现 matlab科研帮手 算法cnngru
    ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，代码获取、论文复现及科研仿真合作可私信。个人主页：Matlab科研工作室个人信条：格物致知。更多Matlab完整代码及仿真定制内容点击智能优化算法神经网络预测雷达通信无线传感器电力系统信号处理图像处理路径规划元胞自动机
  • 数学建模与MATLAB实现：插值技术详解 青橘MATLAB学习 #数学建模Matlab编程实验数学建模matlab开发语言
    引言插值是数学建模与数据分析中的核心技术，广泛应用于信号处理、图像重建、地理信息系统等领域。本文基于一维插值与二维插值的理论框架，结合MATLAB代码实战，系统讲解拉格朗日插值、分段线性插值、三次样条插值等方法，并通过温度预测、地貌分析等案例，帮助读者掌握插值技术的核心原理与实现技巧。一、插值基础理论1.一维插值定义：已知函数在有限点x0,x1,…,xnx_0,x_1,\dots,x_nx0,x1
  • 摄像头模组问题汇总 光学设计培训 光学计算机视觉光学设计光学工程算法
    camera调试名词及问题策略要认识CMOS摄像头的结构。我们通常拿到的是集成封装好的模组，一般由三个部分组成：镜头、感应器和图像信号处理器构成。一般情况下，集成好的模组我们只看到外面的镜头、接口和封装壳，这种一般是固定焦距的。有些厂商只提供芯片，需要自己安装镜头，镜头要选择合适大小的镜头，如果没有夜视要求的话，最好选择带有红外滤光的镜头，因为一般的sensor都能感应到红外光线，如果不滤掉，会对
  • 加速度计信号处理 妄想出头的工业炼药师 信号处理
    【使用DSP滤波器加速速度和位移】使用信号处理算法过滤加速度数据并将其转换为速度和位移研究（Matlab代码实现）_加速度计滤波器-CSDN博客https://wenku.baidu.com/view/622d38b90f22590102020740be1e650e52eacff9.html?_wkts_=1738906719916&bdQuery=%E5%8A%A0%E9%80%9F%E5%BA
  • 锂电池剩余寿命预测 | Matlab基于Transformer-GRU的锂电池剩余寿命预测 天天Matlab代码科研顾问 matlabtransformergru
    ✅作者简介：热爱科研的Matlab仿真开发者，擅长数据处理、建模仿真、程序设计、期刊写作与指导，代码获取、论文复现及科研仿真合作可私信或扫描文章底部二维码。个人主页：Matlab科研工作室个人信条：格物致知。更多Matlab完整代码及仿真定制内容点击智能优化算法神经网络预测雷达通信无线传感器电力系统信号处理图像处理路径规划元胞自动机无人机物理应用机器学习内容介绍锂离子电池作为一种重要的储能装置，在
  • 无人机GPS模块概述！ 云卓SKYDROID 无人机云卓科技科普遥控器高科技GPS
    一、GPS模块原理：GPS模块通过接收来自卫星系统的信号，计算出无人机当前的位置、速度和时间等信息。它主要由接收天线、接收器、信号处理器和电源等组成。接收天线接收来自卫星的GPS信号，接收器将信号转换为数字信号并传输给信号处理器，后者对信号进行解码和处理，最终得出位置信息。工作方式：GPS模块工作的基本原理是三角定位法。它至少需要接收来自三颗卫星的信号，通过测量信号的传播时间和卫星的位置信息，计算
  • 【电力负荷预测】时间卷积双向门控循环单元融合注意力机制TCN-BiGRU-Attention负荷多变量时间序列预测【含Matlab源码 4752期】 Matlab领域 matlab
    ✅博主简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，Matlab项目合作可私信。个人主页：海神之光代码获取方式：海神之光Matlab王者学习之路—代码获取方式⛳️座右铭：行百里者，半于九十。更多Matlab仿真内容点击Matlab图像处理（进阶版）路径规划（Matlab）神经网络预测与分类（Matlab）优化求解（Matlab）语音处理（Matlab）信号处理（Matlab）车间调度
  • 【新书速荐】《Information-Theoretic Radar Signal Processing（信息论雷达信号处理）》 卖酒的雷达算法工程师 概率论
    引言最近，由YujieGu博士和YiminD.Zhang教授主编的新书Information-TheoreticRadarSignalProcessing由Wiley-IEEEPress正式出版。这是信息论雷达信号处理领域的首部专著，全书共分14章，汇集了来自学术界、工业界和政府机构的41位世界知名专家（其中15位为IEEEFellow）的最新研究成果。Information-TheoreticR
  • 数字信号处理Python示例（13）生成方波信号 通信仿真实验室 Python示例数字信号处理信号处理python人工智能
    文章目录前言一、方波信号1.方波的特点2.方波的应用3.方波的产生二、生成方波信号的Python代码三、仿真结果及分析写在后面的话前言从这篇文章开始，将继续给出生成非正弦信号的几个Python示例，包括方波、三角波、锯齿波、sinc函数和高斯信号，这几个都是在信号处理理论与应用中非常重要的信号。一、方波信号方波是一种非正弦周期波形，它的特征是在每个周期内电压或电流快速地在两个电平之间切换，通常是在
  • SCI一区级 | SAO-CNN-LSTM-Mutilhead-Attention雪消融算法优化卷积长短期记忆神经网络融合多头注意力机制多变量时间序列预测Matlab实现 天天Matlab代码科研顾问 神经网络cnnlstm
    ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，代码获取、论文复现及科研仿真合作可私信。个人主页：Matlab科研工作室个人信条：格物致知。更多Matlab完整代码及仿真定制内容点击智能优化算法神经网络预测雷达通信无线传感器电力系统信号处理图像处理路径规划元胞自动机无人机物理应用机器学习内容介绍光伏发电作为一种清洁能源，在能源转型中扮演着至关重要的角色。准确预测光伏发电量对于提高
  • RK3568的ISP功能 沐风_ZTL 接口隔离原则人工智能RK3568ISP
    RockchipRK3568处理器的ISP（图像信号处理器）功能专为提升图像质量设计，适用于多种视觉应用场景。以下是其ISP功能的详细解析：核心功能与特性多摄像头支持配置灵活：支持单摄像头最高13MP（30fps），或双8MP摄像头（30fps），适用于多目监控或立体视觉。接口兼容：支持MIPI-CSI（2-4Lane）、DVP并行接口、LVDS等，适配多种传感器。图像增强处理3D降噪（3DNR）
  • （62）使用RLS自适应滤波器进行系统辨识的MATLAB仿真 通信仿真实验室 matlab信号处理通信系统通信算法开发语言自适应滤波器RLS
    文章目录前言一、基本概念二、RLS算法原理三、RLS算法的典型应用场景四、MATLAB仿真代码五、仿真结果1.滤波器的输入信号、参考信号、输出信号、误差信号2.对未知系统进行辨识得到的系数总结与后续前言RLS（递归最小二乘）自适应滤波器是一种用于系统辨识和信号处理的算法，其原理基于最小二乘法。系统辨识是指从输入输出数据中估计或建模一个动态系统的过程。在RLS自适应滤波器中，目的是找到滤波器系数，使
  • nginx技术底层 沉默monkey nginxphp网络
    提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、进程模型二、事件驱动与异步IO事件通知机制多路复用非阻塞IO事件处理循环四、内存管理内存池机制对象复用五、零拷贝技术六、模块化设计七、与操作系统交互系统调用信号处理内存映射前言nginx采用异步，事件驱动，非阻塞I/O模型，旨在应对高并发连接请求，保证低延迟和高吞吐量，设计理念包括：异步事件驱动：通过事件通知机制（ep
  • JVM致命错误日志详解 「已注销」 JAVAjvmjava
    文章目录文件描述文件位置文件头错误信息记录JVM运行信息崩溃原因错误信息线程描述线程信息信号信息计数器信息机器指令内存映射信息线程堆栈其他信息进程描述线程列表虚拟机状态互斥锁/管程堆概览卡表和本地代码缓存编译事件GC事件逆向优化事件内部错误事件内存信息虚拟机参数和环境变量信号处理器系统信息操作系统内存信息CPU信息总结最近一段时间生产环境频繁出问题，每次都会生成一个hs_err_pid*.log文
  • Python：谈谈常规滤波器(带通、低通、高通、带阻)的用法 我不是哆啦A梦 Python信号处理python算法
    一、滤波器的作用滤波器在信号处理中用于移除或减少信号中的噪声，同时保持信号的某些特性。滤波器通常用于音频、视频和图像处理等领域。滤波器根据其designedfordifferentpurposesandcanbedividedintoseveraltypes,suchaslowpassfilters,highpassfilters,bandpassfilters,andbandstopfilter
  • Linux Signal Handler 死锁问题 c++linux
    Linux上的程序可以注册信号处理函数(signalhandler)用于处理信号，signalhandler不能随便调用，否则可能一不留神就死锁了，我们曾在这个问题上反复踩坑。这篇文章我们来讲LinuxSignalHandler的死锁问题。signalhandler常见的使用场景是处理程序的退出。比如，一个后台运行的程序，可以注册一个处理SIGTERM的signalhandler，在收到这个信号后
  • DSP定点运算之数字信号处理算法的定点化及其C语言仿真（转） u010748717
    DSP广义上指数字信号处理理论(DigitalSignalProcessing)，狭义上指数字信号处理器(DigitalSignalProcessor)。数字信号处理理论广泛应用于语音、图象、遥测数据、电机控制等各个方面。现代个人通信、互联网、多媒体应用的飞速发展又推动着数字信号处理理论的进一步发展。现代信号处理（ASP）算法越来越复杂，处理的数据量越来越庞大。由于体系结构的限制，通用微处理器并不
  • 低通滤波算法的数学原理和C语言实现 mftang 自动化控制与算法算法
    目录概述1原理介绍1.1基本概念1.2一阶RC低通滤波器模型2C语言完整实现2.1滤波器结构体定义2.2初始化函数2.3滤波计算函数3应用示例3.1噪声信号滤波3.2输出效果对比3.3关键参数选择指南4性能优化技巧4.1定点数优化4.2抗溢出处理5多阶滤波器扩展概述低通滤波是一种信号处理算法，用于滤除高频成分，只保留低频成分。其原理是将输入信号通过一个滤波器，滤除高于某个截止频率的频率成分，只保留
  • 音视频开发成长之路与音视频知识点总结 Linux服务器开发 音视频开发webrtcffmpeg音视频开发流媒体服务器开发webrtcFFmpeg嵌入式音视频开发
    音视频涉及语音信号处理、数字图像处理、信息论、封装格式、编解码、流媒体协议、网络传输、渲染、算法等。在现实生活中，音视频发挥着越来越重要的作用，如视频会议、直播、短视频、播放器、语音聊天等。所以从事音视频开发是一件有意义的事情，机遇和挑战并存。本文将从：音视频开发基础、音视频高级成长、音视频工作方向、音视频开源库、音视频相关书籍，配套的学习资源等几个方面来进行介绍。那么我们该如何系统的学习音视频开
  • delta-sigma ADC基础知识(一) 通信射频老兵 5G射频工程经验分享
    模拟技术在信号处理领域长期占据主导地位，但数字技术正逐渐渗透这一领域。德尔塔-西格玛（DS）模数转换器（ADC）的设计大约四分之三是数字部分，四分之一是模拟部分。DSADC现在非常适合将模拟信号从直流（DC）到数兆赫兹的宽频率范围内进行转换。这些转换器基本上由一个过采样调制器后跟一个数字/抽取滤波器组成，共同产生高分辨率的数据流输出。本文分两部分深入探讨DSADC的核心。第一部分将探讨DS调制器的
  • 初五迎财神！——Python代码实现“元宝多多“，财神看了都说妙 MatpyMaster python
    初五迎财神，讲究的是"抢头彩"：开市、扫穷、接元宝。祈求财运亨通、事业顺利。按照习俗，家家户户都会燃放鞭炮、点灯笼、摆设祭品，以示虔诚。下面小编基于Python，给大家安利了一款"元宝多多"小游戏，祝大家蛇年健康平安，吉祥如意。在新的一年中不断进步，永远快乐。”初五迎财神！——Python代码实现"元宝多多"，财神看了都说妙最后：小编会不定期发布相关设计内容包括但不限于如下内容:信号处理、通信仿真
  • 【中科院1区】Matlab实现黏菌优化算法SMA-RF锂电池健康状态估计算法研究 matlab科研助手 matlab算法开发语言
    ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，代码获取、论文复现及科研仿真合作可私信。个人主页：Matlab科研工作室个人信条：格物致知。更多Matlab完整代码及仿真定制内容点击智能优化算法神经网络预测雷达通信无线传感器电力系统信号处理图像处理路径规划元胞自动机无人机物理应用机器学习内容介绍摘要锂离子电池作为一种重要的储能器件，在电动汽车、便携式电子设备等领域发挥着至关重要的
  • 基于能量检测的语音信号端点检测 FPGA 实现 鱼弦 人工智能时代fpga开发
    基于能量检测的语音信号端点检测FPGA实现介绍语音信号端点检测（VoiceActivityDetection,VAD）是语音处理中的一个重要步骤，用于确定语音信号的起始和结束点。基于能量检测的方法通过计算语音信号的能量来识别活跃语音段。FPGA的并行处理能力使其非常适合用于实时的语音信号处理。应用使用场景语音识别系统：提高识别准确性，减少处理非语音片段。通信设备：降低带宽需求，通过仅传输语音部分节
  • java杨辉三角 3213213333332132 java基础
    package com.algorithm; /** * @Description 杨辉三角 * @author FuJianyong * 2015-1-22上午10:10:59 */ public class YangHui { public static void main(String[] args) { //初始化二维数组长度 int[][] y
  • 《大话重构》之大布局的辛酸历史 白糖_ 重构
    《大话重构》中提到“大布局你伤不起”，如果企图重构一个陈旧的大型系统是有非常大的风险，重构不是想象中那么简单。我目前所在公司正好对产品做了一次“大布局重构”，下面我就分享这个“大布局”项目经验给大家。   背景         公司专注于企业级管理产品软件，企业有大中小之分，在2000年初公司用JSP/Servlet开发了一套针对中
  • 电驴链接在线视频播放源码 dubinwei 源码电驴播放器视频ed2k
    本项目是个搜索电驴（ed2k）链接的应用,借助于磁力视频播放器（官网： http://loveandroid.duapp.com/ 开放平台），可以实现在线播放视频，也可以用迅雷或者其他下载工具下载。 项目源码： http://git.oschina.net/svo/Emule,动态更新。也可从附件中下载。 项目源码依赖于两个库项目，库项目一链接： http://git.oschina.
  • Javascript中函数的toString()方法 周凡杨 JavaScriptjstoStringfunctionobject
    简述     The toString() method returns a string representing the source code of the function.     简译之，Javascript的toString()方法返回一个代表函数源代码的字符串。 句法     function.
  • struts处理自定义异常 g21121 struts
    很多时候我们会用到自定义异常来表示特定的错误情况，自定义异常比较简单，只要分清是运行时异常还是非运行时异常即可，运行时异常不需要捕获，继承自RuntimeException，是由容器自己抛出，例如空指针异常。 非运行时异常继承自Exception，在抛出后需要捕获，例如文件未找到异常。 此处我们用的是非运行时异常，首先定义一个异常LoginException: /** * 类描述：登录相
  • Linux中find常见用法示例 510888780 linux
    Linux中find常见用法示例 ·find   path   -option   [   -print ]   [ -exec   -ok   command ]   {} \; find命令的参数；
  • SpringMVC的各种参数绑定方式 Harry642 springMVC绑定表单
    1. 基本数据类型(以int为例，其他类似)： Controller代码： @RequestMapping("saysth.do") public void test(int count) { } 表单代码： <form action="saysth.do" method="post&q
  • Java 获取Oracle ROWID aijuans javaoracle
    A ROWID is an identification tag unique for each row of an Oracle Database table. The ROWID can be thought of as a virtual column, containing the ID for each row. The oracle.sql.ROWID class i
  • java获取方法的参数名 antlove javajdkparametermethodreflect
    reflect.ClassInformationUtil.java package reflect; import javassist.ClassPool; import javassist.CtClass; import javassist.CtMethod; import javassist.Modifier; import javassist.bytecode.CodeAtt
  • JAVA正则表达式匹配 查找 替换 提取操作 百合不是茶 java正则表达式替换提取查找
    正则表达式的查找;主要是用到String类中的split();       String str;      str.split();方法中传入按照什么规则截取,返回一个String数组   常见的截取规则: str.split("\\.")按照.来截取 str.
  • Java中equals()与hashCode()方法详解 bijian1013 javasetequals()hashCode()
    一.equals()方法详解     equals()方法在object类中定义如下：  public boolean equals(Object obj) { return (this == obj); }    很明显是对两个对象的地址值进行的比较（即比较引用是否相同）。但是我们知道，String 、Math、I
  • 精通Oracle10编程SQL(4)使用SQL语句 bijian1013 oracle数据库plsql
    --工资级别表 create table SALGRADE ( GRADE NUMBER(10), LOSAL NUMBER(10,2), HISAL NUMBER(10,2) ) insert into SALGRADE values(1,0,100); insert into SALGRADE values(2,100,200); inser
  • 【Nginx二】Nginx作为静态文件HTTP服务器 bit1129 HTTP服务器
     Nginx作为静态文件HTTP服务器 在本地系统中创建/data/www目录，存放html文件(包括index.html) 创建/data/images目录，存放imags图片 在主配置文件中添加http指令   http { server { listen 80; server_name
  • kafka获得最新partition offset blackproof kafkapartitionoffset最新
    kafka获得partition下标，需要用到kafka的simpleconsumer   import java.util.ArrayList; import java.util.Collections; import java.util.Date; import java.util.HashMap; import java.util.List; import java.
  • centos 7安装docker两种方式 ronin47
          第一种是采用yum 方式              yum install -y docker           
  • java-60-在O(1)时间删除链表结点 bylijinnan java
    public class DeleteNode_O1_Time { /** * Q 60 在O(1)时间删除链表结点 * 给定链表的头指针和一个结点指针(!!)，在O(1)时间删除该结点 * * Assume the list is: * head->...->nodeToDelete->mNode->nNode->..
  • nginx利用proxy_cache来缓存文件 cfyme cache
    user  zhangy users; worker_processes 10; error_log  /var/vlogs/nginx_error.log  crit; pid        /var/vlogs/nginx.pid; #Specifies the value for ma
  • [JWFD开源工作流]JWFD嵌入式语法分析器负号的使用问题 comsci 嵌入式
        假如我们需要用JWFD的语法分析模块定义一个带负号的方程式，直接在方程式之前添加负号是不正确的，而必须这样做：     string str01 = "a=3.14;b=2.71;c=0;c-((a*a)+(b*b))"     定义一个0整数c,然后用这个整数c去
  • 如何集成支付宝官方文档 dai_lm android
    官方文档下载地址 https://b.alipay.com/order/productDetail.htm?productId=2012120700377310&tabId=4#ps-tabinfo-hash 集成的必要条件 1. 需要有自己的Server接收支付宝的消息 2. 需要先制作app，然后提交支付宝审核，通过后才能集成 调试的时候估计会真的扣款，请注意
  • 应该在什么时候使用Hadoop datamachine hadoop
    原帖地址：http://blog.chinaunix.net/uid-301743-id-3925358.html 存档，某些观点与我不谋而合，过度技术化不可取，且hadoop并非万能。 --------------------------------------------万能的分割线-------------------------------- 有人问我，“你在大数据和Hado
  • 在GridView中对于有外键的字段使用关联模型进行搜索和排序 dcj3sjt126com yii
    在GridView中使用关联模型进行搜索和排序 首先我们有两个模型它们直接有关联: class Author extends CActiveRecord { ... } class Post extends CActiveRecord { ... function relations() { return array( '
  • 使用NSString 的格式化大全 dcj3sjt126com Objective-C
    格式定义The format specifiers supported by the NSString formatting methods and CFString formatting functions follow the IEEE printf specification; the specifiers are summarized in Table 1. Note that you c
  • 使用activeX插件对象object滚动有重影 蕃薯耀 activeX插件滚动有重影
      使用activeX插件对象object滚动有重影   <object style="width:0;" id="abc" classid="CLSID:D3E3970F-2927-9680-BBB4-5D0889909DF6" codebase="activex/OAX339.CAB#
  • SpringMVC4零配置 hanqunfeng springmvc4
    基于Servlet3.0规范和SpringMVC4注解式配置方式，实现零xml配置，弄了个小demo，供交流讨论。     项目说明如下： 1.db.sql是项目中用到的表，数据库使用的是oracle11g 2.该项目使用mvn进行管理，私服为自搭建nexus,项目只用到一个第三方 jar，就是oracle的驱动； 3.默认项目为零配置启动，如果需要更改启动方式，请
  • 《开源框架那点事儿16》：缓存相关代码的演变 j2eetop 开源框架
    问题引入 上次我参与某个大型项目的优化工作，由于系统要求有比较高的TPS，因此就免不了要使用缓冲。 该项目中用的缓冲比较多，有MemCache，有Redis，有的还需要提供二级缓冲，也就是说应用服务器这层也可以设置一些缓冲。 当然去看相关实现代代码的时候，大致是下面的样子。 [java] view plain copy print ? public vo
  • AngularJS浅析 kvhur JavaScript
    概念 AngularJS is a structural framework for dynamic web apps. 了解更多详情请见原文链接：http://www.gbtags.com/gb/share/5726.htm Directive 扩展html，给html添加声明语句，以便实现自己的需求。对于页面中html元素以ng为前缀的属性名称，ng是angular的命名空间
  • 架构师之jdk的bug排查(一)---------------split的点号陷阱 nannan408 split
    1.前言.    jdk1.6的lang包的split方法是有bug的,它不能有效识别A.b.c这种类型,导致截取长度始终是0.而对于其他字符,则无此问题.不知道官方有没有修复这个bug. 2.代码 String[] paths = "object.object2.prop11".split("'"); System.ou
  • 如何对10亿数据量级的mongoDB作高效的全表扫描 quentinXXZ mongodb
      本文链接:  http://quentinXXZ.iteye.com/blog/2149440 一、正常情况下，不应该有这种需求 首先，大家应该有个概念，标题中的这个问题，在大多情况下是一个伪命题，不应该被提出来。要知道，对于一般较大数据量的数据库，全表查询，这种操作一般情况下是不应该出现的，在做正常查询的时候，如果是范围查询，你至少应该要加上limit。 说一下，
  • C语言算法之水仙花数 qiufeihu c算法
    /** * 水仙花数 */ #include <stdio.h> #define N 10 int main() { int x,y,z; for(x=1;x<=N;x++) for(y=0;y<=N;y++) for(z=0;z<=N;z++) if(x*100+y*10+z == x*x*x
  • JSP指令 wyzuomumu jsp
    jsp指令的一般语法格式： <%@ 指令名 属性 =”值 ” %> 常用的三种指令： page,include,taglib page指令语法形式： <%@ page 属性 1=”值 1” 属性 2=”值 2”%> include指令语法形式： <%@include file=”relative url”%> (jsp可以通过 include
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他