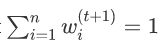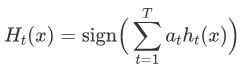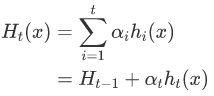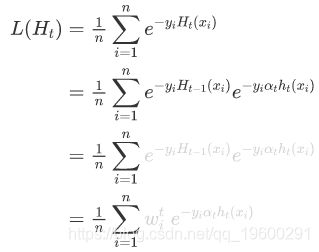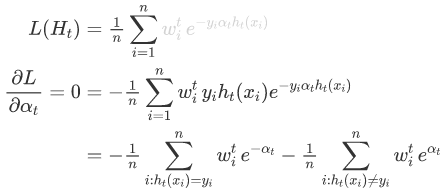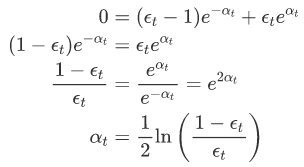原文链接:http://tecdat.cn/?p=24421
AdaBoost是?
Boosting指的是机器学习元算法系列,它将许多 "弱 "分类器的输出合并成一个强大的 "集合",其中每个弱分类器单独的错误率可能只比随机猜测好一点。
AdaBoost这个名字代表了自适应提升,它指的是一种特殊的提升算法,在这种算法中,我们适合一连串的 "树桩"(有一个节点和两个叶子的决策树),并根据它们预测的准确程度对它们的最终投票进行加权。在每个迭代之后,我们对数据集进行重新加权,对那些被前一个弱学习者错误分类的数据点给予更大的重视,这样,这些数据点在迭代t+1期间就会得到 "特别关注"。
它与随机森林相比如何?
特点
随机森林
AdaBoost
深度
无限(一棵完整的树)
树桩(带有 2 个叶子的单个节点)
树木生长
独立
依次
投票
相同
加权
AdaBoost 算法
B) 对于每次迭代 t:
绘图
我们将使用下面的函数来可视化我们的数据点,并可选择覆盖拟合 AdaBoost 模型的决策边界。
def plot(X: np.ndaay,
y: np.ndrry,
cf=None) -> None:
""" 绘制2D的±个样本,可选择决策边界 """
if not ax:
fig, ax = plt.sults(fgsze=(5, 5), di=100)
pad = 1
x\_min, x\_max = X\[:, 0\].min() - pad, X\[:, 0\].max() + pad
y\_min, y\_max = X\[:, 1\].min() - pad, X\[:, 1\].max() + pad
if saligs is not None:
sies = np.array(spl_wigts) * X.hae\[0\] * 100
else:
sze = np.oes(sape=X.shpe\[0\]) * 100
if cf:
xx, yy = np.ehrid(n.aange(x\_min, x\_max, plot_step),
p.aang(y\_min, y\_max, plot_step))
pdt(np.c_\[xx.ravel(), yy.ravel()\])
# 如果所有的预测都是正类,则相应地调整颜色图。
if list(np.niue(Z)) == \[1\]:
colors = \['r'\]
else:
colors = \['b', 'r'\]
ax.st\_im(in+0.5, \_ax-0.5)
ax.st_lm(ymin+0.5, yax-0.5)数据集
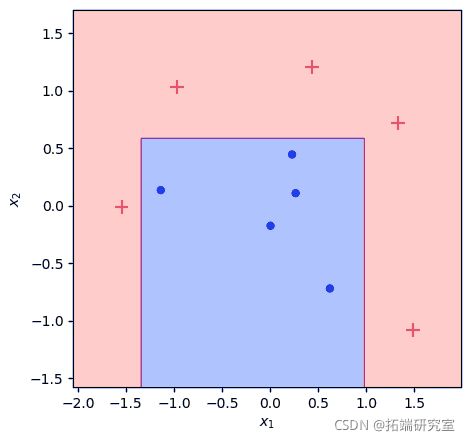
我们将使用类似的方法生成一个数据集 ,但使用较少的数据点。这里的关键是我们想要两个不可线性分离的类,因为这是 AdaBoost 的理想用例。
def maketat(n: it = 100, rased: it = None):
""" 生成一个用于评估AdaBoost分类器的数据集 """
nclas = int(n/2)
if ranmed:
np.ram.sed(rndoed)
X, y = me\_gainqnes(n=n, n\_fees=2, n_css=2)
plot(X, y)使用 scikit-learn 进行基准测试
让我们通过从scikit-learn导入AdaBoostClassifier,并将其拟合到我们的数据集上,来建立一个基准,看看我们的模型的输出应该是什么样子的。
from skarn.esele import AdosClaser
bnh = Adostlier(netrs=10, atm='SAMME').fit(X, y)
plat(X, y, bech)
tnr = (prdict(X) != y).man()![]()
分类器在 10 次迭代中完全拟合训练数据集,我们数据集中的数据点被合理分离。
编写自己的AdaBoost分类器
下面是我们的AdaBoost分类器的框架代码。拟合模型后,我们将把所有的关键属性保存到类中--包括每次迭代的样本权重--这样我们就可以在以后检查它们,以了解我们的算法在每一步的作用。
下表显示了我们将使用的变量名称和前面在算法描述中使用的数学符号之间的映射。
变量
数学
sampleweight
wi(t)
stump
ht(x)
stumpweight
αt
error
εt
predict(X)
Ht(x)
class AdBst:
""" AdaBoost分类器 """
def \_\_init\_\_(self):
self.sump = None
self.stup_weght = None
self.erro = None
self.smle_weih = None
def \_ceck\_X_y(self, X, y):
""" 验证关于输入数据格式的假设"""
assrt st(y) == {-1, 1}
reurn X, y拟合模型
回想一下我们的算法来拟合模型:
- 找到
ht(x)最小化的弱学习 器 .
. - 我们根据其准确性为弱学习器设置权重:

- 增加错误分类观察的权重:
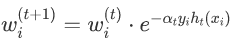 . 注意
. 注意 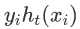 当假设与标签一致时将评估为 +1,当它与标签不一致时将评估为 -1。
当假设与标签一致时将评估为 +1,当它与标签不一致时将评估为 -1。 - 重新归一化权重,使得
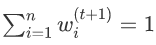 .
.
下面的代码本质上是上面的一对一的实现,但是有几点需要注意:
- 由于这里的重点是理解AdaBoost的集合元素,我们将调用DecinTeassfir(mxdpth=1, mlefnes=2)实现挑选每个ht(x)的逻辑。
- 我们在 for 循环之外设置初始统一样本权重,并在每次迭代 t 内设置 t+1 的权重,除非它是最后一次迭代。我们在这里特意在拟合模型上保存一组样本权重,以便我们以后可以在每次迭代时可视化样本权重。
def ft(slf, X: narry, y: ndray, ites: int):
""" 使用训练数据拟合模型 """
X, y = slf.\_chck\_X_y(X, y)
n = X.shpe\[0\]
# 启动Numpy数组
self.smle_wegts = np.zos(shpe=(itrs, n))
self.tumps = np.zeos(she=iters, dtpe=obect)
# 均匀地初始化权重
sef.sampewegts\[0\] = np.one(shpe=n) / n
for t in range(iters):
# 拟合弱学习器
fit(X, y, smpe\_eght=urrsmle\_igts)
# 从弱学习者的预测中计算出误差和树桩权重
predict(X)
err = cu_seghts\[(pred != y)\].sum()# / n
weiht = np.log((1 - err) / err) / 2
# 更新样本权重
newweis = (
crrawe * np.exp(-sum_wiht * y * tupd)
)
# 如果不是最终迭代,则更新t+1的样本权重
if t+1 < ies:
sef.smpe\_wit\[t+1\] = ne\_saml_wigt
# 保存迭代的结果
sef.sups\[t\] = tump做出预测
我们通过采取“加权多数投票”来做出最终预测,计算为每个树桩的预测及其相应树桩权重的线性组合的符号 (±)。
def pedc(self, X):
""" 使用已经拟合的模型进行预测 """
supds = np.aray(\[stp.pect(X) for sump in slf.stps\])
return np.sgn(np.dt(self.tum_whts, sumpreds))表现
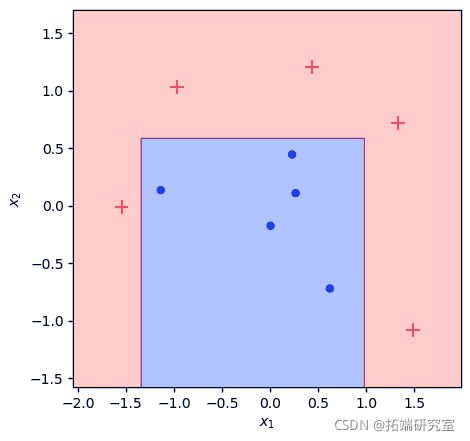
现在让我们把所有东西放在一起,用与我们的基准测试相同的参数来拟合模型。
# 将我们单独定义的函数指定为分类器的方法
AaBt.fit = fit
Adostreit = pedct
plot(X, y, clf)
err = (clf.prdc(X) != y).mean()![]()
不错! 我们取得了与sklearn基准完全相同的结果。我挑选了这个数据集来展示AdaBoost的优势,但你可以自己运行这个笔记本,看看它是否与输出结果相匹配,无论起始条件如何。
可视化
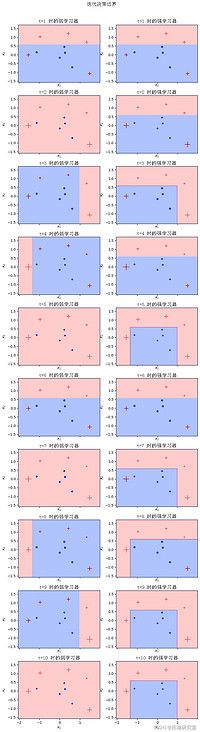
由于我们把所有的中间变量作为数组保存在我们的拟合模型中,我们可以使用下面的函数来可视化我们的集合学习器在每个迭代t的演变过程。
- 左栏显示了所选择的 "树桩 "弱学习器,它与ht(x)相对应。
- 右边一栏显示了到目前为止的累积强学习器。 Ht(x)。
- 数据点标记的大小反映了它们的相对权重。在上一次迭代中被错误分类的数据点将被更多地加权,因此在下一次迭代中显得更大。
def truost(clf, t: int):
""" AdaBoost的拟合,直到(并包括)某个特定的迭代。 """
nwwghts = clf.suweighs\[:t\]
def plotost(X, y, clf, iters=10):
""" 在每个迭代中绘制出弱学习者和累积强学习者。 """
# 更大的网格
fig, axs = subplos(fisze=(8,ters*3),
nrows=iers,
ncls=2,
shaex=True,
dpi=100)
# 绘制弱学习者
plotot(X, y, cf.\[i\],
saplweghs=clf.saple_wigts\[i\],
aoat=False, a=ax1)
#绘制强学习者
truost(clf, t=i + 1)
pltot(X, y, tun_cf,
weights=smplweih\[i\], ax=ax2)
plt.t_aot()为什么有些迭代没有决策边界?
您可能会注意到,我们的弱学习器在迭代 t=2,5,7,10 时将所有点归类为正。发生这种情况是因为给定当前样本权重,只需将所有数据点预测为正值即可实现最低误差。请注意,在上面这些迭代的每个图中,负样本被按比例更高权重的正样本包围。
没有办法画出一个线性决策边界来正确分类任何数量的负面数据点,而不对正面样本的更高累积权重进行错误分类。不过这并不能阻止我们的算法收敛。所有的负数点都被错误分类,因此样本权重增加。这种权重的更新使得下一次迭代的弱学习者能够发现一个有意义的决策边界。
为什么我们对 alpha_t 使用那个特定的公式?
为什么我们使用这个特定的值 αt?我们可以证明选择 ![]() 最小化在训练集上的指数损失
最小化在训练集上的指数损失 ![]() 。
。
忽略符号函数,我们H 在迭代时 的强学习器 t 是弱学习器的加权组合 h(x)。在任何给定的迭代中 t,我们可以Ht(x) 递归地将其定义 为迭代时的值 t−1 加上当前迭代的加权弱学习器。
我们应用于 H 的损失函数是所有 n 个数据点的平均损失。可以替代 的递归定义 Ht(x),并使用恒等式分割指数项 ![]() .
.
现在我们取损失函数关于 的导数 αt 并将其设置为零以找到最小化损失函数的参数值。可以将总和分为两个:case where ht(xi)=yi 和 case where ht(xi)≠yi。
最后,我们认识到权重之和等同于我们前面讨论的误差计算:∑Dt(i)=ϵt。进行置换,然后进行代数操作,我们就可以分离出αt。
进一步阅读
- sklearn.ensemble.AdaBoostClassifier – 官方 scikit-learn 文档
最受欢迎的见解
3.python中使用scikit-learn和pandas决策树
7.用机器学习识别不断变化的股市状况——隐马尔可夫模型的应用