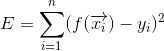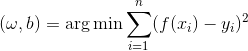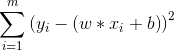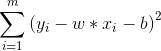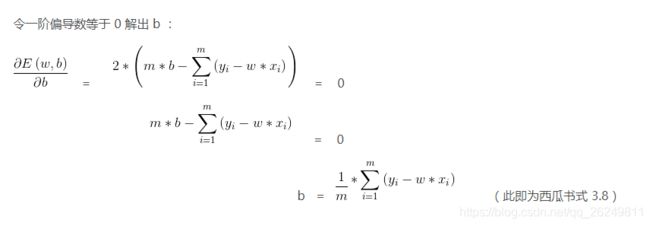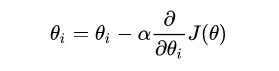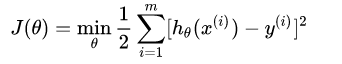深度不学习——————线性回归
线性回归¶
主要内容包括:
- 线性回归的基本要素
- 线性回归模型从零开始的实现
1.线性回归的基本要素:
现在给定一个数据集,包含n个样本,x为属性表述的一个向量,维数为d,y为在向量x下的实际结果:
![]()
上式表示的是第i个样本的属性描述向量,x1到xd表示d个不同的属性。我们要利用这些属性综合来进行数据分析,根据不同属性的“权重”以及最后所有属性乘以权重的和给出一个评分,然后比较评分和预先设定的阈值来判定结果是否符合预期,换句话说就是真实值和预测值是否比较接近。我们可以得到以下公式:
1.  2.
2. 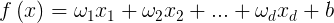
现在我们有一个数据集![]() 。现在,我们需要利用小样本来学习。学习的最终目的是使得预测值f(x)和实际值y尽量接近,这里我们使用残差平方和:
。现在,我们需要利用小样本来学习。学习的最终目的是使得预测值f(x)和实际值y尽量接近,这里我们使用残差平方和:
我们计算每个样本的预测值和实际值的差,再求平方,最后所有样本求和,我们最终目的是使f(x)和y的值尽量接近,所以,这相当于要求残差平方和E必须最小:
当E最小时,我们就得到一组(w,b),这就是我们最后学习得到的参数。接下来就是怎么求这个最值,常见的方法有“最小二乘”和“梯度下降”。
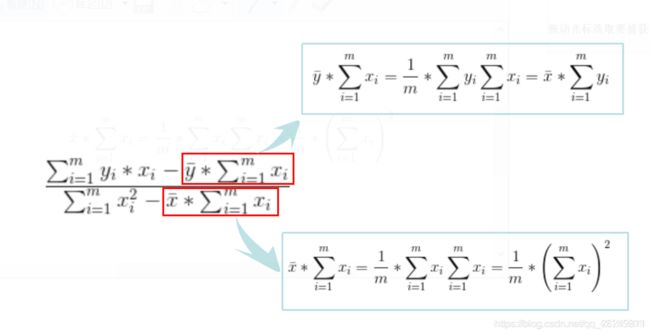
最小二乘法导出损失函数 :
参考:https://blog.csdn.net/yeshen4328/article/details/79867683
参考:https://blog.csdn.net/qq_42185999/article/details/102941535
梯度下降法:
简言之,一个公式解决你的所有疑惑:
1.如何理解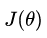 这个函数
这个函数
可以简单的这样理解,我们要假设的模型最终要和现实世界的模型最好的吻合,这也是我们的初衷,如何来衡量吻合的效果呢?我们用方差来表示吻合的效果,这个其实也叫做损失函数,当我们把损失降低到最小的时候,吻合的效果是最好的。这个和我们一开始提出的下山路径规划是一个思路,所以就可以用同一种方法来求解了。其实这个方法就是用来求解最小值问题的。
2.那么为什么要走最快的路径呢?走其他路径不是也可以到达最低点吗?
答案是可以,通过其他的路径也可以到达最低点,在生活中确实也是这样的,但是根据我们从高中就建立起来的数学观念,貌似我们只学过两种求极值的方法,其一是根据曲线的特性,其二是求导。很明显,这个问题没有给定的曲线,所以我们只能用第二种方式来求解最值了。
当然如果你发现了一个新的求解极值的方式,也许你就是那个可以改变世界的人。期待你的进一步研究。
推导1:

参考:https://www.jianshu.com/p/93d9fea7f4c2
梯度下降法和最小二乘法相比,梯度下降法需要选择步长,而最小二乘法不需要。梯度下降法是迭代求解,最小二乘法是计算解析解。如果样本量不算很大,且存在解析解,最小二乘法比起梯度下降法要有优势,计算速度很快。但是如果样本量很大,用最小二乘法由于需要求一个超级大的逆矩阵,这时就很难或者很慢才能求解解析解了,使用迭代的梯度下降法比较有优势。
梯度下降法和牛顿法/拟牛顿法相比,两者都是迭代求解,不过梯度下降法是梯度求解,而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言,使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。
主要代码:
# import packages and modules
import torch
from IPython import display
from matplotlib import pyplot as plt
import numpy as np
import random
#生成数据集
# set input feature number
num_inputs = 2
# set example number
num_examples = 1000
# set true weight and bias in order to generate corresponded label
true_w = [2, -3.4]
true_b = 4.2
features = torch.randn(num_examples, num_inputs,
dtype=torch.float32)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),
dtype=torch.float32)
#读取数据集
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) # random read 10 samples
for i in range(0, num_examples, batch_size):
j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # the last time may be not enough for a whole batch
yield features.index_select(0, j), labels.index_select(0, j)
for X, y in data_iter(batch_size=10, features, labels):
print(X, '\n', y)
break
#初始化模型参数
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
#tensor([0.], requires_grad=True)
#定义模型
#定义用来训练参数的训练模型:
def linreg(X, w, b):
return torch.mm(X, w) + b
#定义损失函数
#我们使用的是均方误差损失函数:
def squared_loss(y_hat, y):
return (y_hat - y.view(y_hat.size())) ** 2 / 2
#定义优化函数
#在这里优化函数使用的是小批量随机梯度下降:
def sgd(params, lr, batch_size):
for param in params:
param.data -= lr * param.grad / batch_size # ues .data to operate param without gradient track
#训练
#当数据集、模型、损失函数和优化函数定义完了之后就可来准备进行模型的训练了。
# super parameters init
lr = 0.03
num_epochs = 5
net = linreg
loss = squared_loss
# training
for epoch in range(num_epochs): # training repeats num_epochs times
# in each epoch, all the samples in dataset will be used once
# X is the feature and y is the label of a batch sample
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y).sum()
# calculate the gradient of batch sample loss
l.backward()
# using small batch random gradient descent to iter model parameters
sgd([w, b], lr, batch_size)
# reset parameter gradient
w.grad.data.zero_()
b.grad.data.zero_()
train_l = loss(net(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
#epoch 1, loss 0.050399
#epoch 2, loss 0.000223
#epoch 3, loss 0.000052
#epoch 4, loss 0.000051
#epoch 5, loss 0.000051
更多代码内容请关注伯禹教育