动手学深度学习——线性回归的简洁实现

1、导入的数据包

import numpy as np
import torch
import torch.utils.data as Data #PyTorch提供了 data 包来读取数据。由于 data 常⽤作变量名，我们将导⼊的 data 模块⽤ Data 代替。
from torch import nn, optim
from torch.nn import init

2、生成数据集，其中features是训练数据特征，labels是标签。

num_inputs=2  #输入的个数
num_examples=1000 #训练数据集
true_w=[2,-3.4] #真实权重
true_b=4.2 #真实偏差
features=torch.tensor(np.random.normal(0,1,(num_examples,num_inputs)),dtype=torch.float)
# 均值为0，方差为1的随机数 ，有num_examples个样本，列数为num_inputs
labels=true_w[0]*features[:,0]+true_w[1]*features[:,1]+true_b
# lables就等于w的每列乘以features的每列然后相加，最后加上偏差true_b；
labels+=torch.tensor(np.random.normal(0,0.01,size=labels.size()),dtype=torch.float)
# 加入了一个噪音，均值为0，方差为0.01，形状和lables的长度是一样的

3、读取数据

PyTorch提供了 data 包来读取数据。

batch_size=10  #10个数据样本的⼩批量
dataset=Data.TensorDataset(features,labels) #将训练数据的特征和标签组合
data_iter=Data.DataLoader(dataset,batch_size,shuffle=True) #随机读取小批量
#接下来读取并打印第一个小批量数据样本
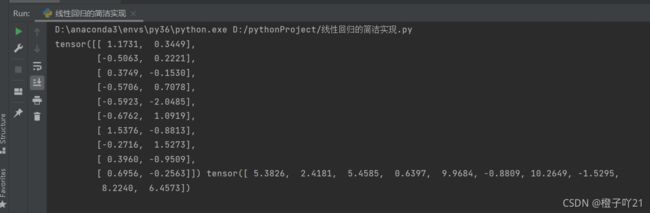
for X,y in data_iter:
    print(X,y)
    break

 

4、定义模型 ，如何⽤ nn.Module 实现⼀个线性回归模型

class LinearNet(nn.Module): #nn是神经网络的缩写
    def __init__(self,n_feature):
        super(LinearNet, self).__init__()
        self.linear=nn.Linear(n_feature,1)
    def forward(self,x): #返回输出的向前传播方法
        y=self.linear(x)
        return y
net =LinearNet(num_inputs)
print(net)

事实上我们还可以⽤ nn.Sequential 来更加⽅便地搭建⽹络， Sequential 是⼀个有序的容器，⽹络
层将按照在传⼊ Sequential 的顺序依次被添加到计算图中。

# 写法⼀
net = nn.Sequential(
 nn.Linear(num_inputs, 1)
 # 此处还可以传⼊其他层
 )
# 写法⼆
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......
# 写法三
from collections import OrderedDict
net = nn.Sequential(OrderedDict([
 ('linear', nn.Linear(num_inputs, 1))
 # ......
 ]))
print(net)
print(net[0])

 

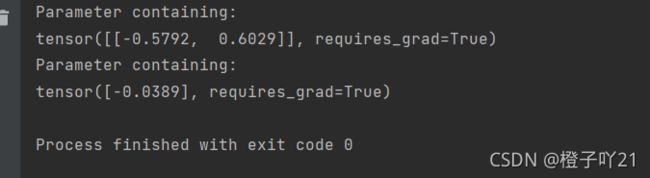
可以通过 net.parameters() 来查看模型所有的可学习参数，此函数将返回⼀个⽣成器。

for param in net.parameters():
 print(param)

5、初始化模型

#init 是 initializer(初始化设定) 的缩写形式
init.normal_(net[0].weight,mean=0,std=0.01) #通过 init.normal_ 将权重参数每个元素初始化为随机采样于均值为0、标准差为0.01的正态分布
init.constant_(net[0].bias,val=0) #偏差会初始化为零

6、定义损失函数

loss=nn.MSELoss()#计算均方误差使用的是MSELoss类，也称为平方L2范数

7、定义优化算法

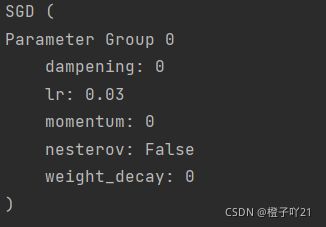
#torch.optim 模块提供了很多常⽤的优化算法⽐如SGD、Adam和RMSProp等
optimizer=optim.SGD(net.parameters(),lr=0.03) #拿出所有的参数w和b，学习率为0.03
print(optimizer)

关于学习率

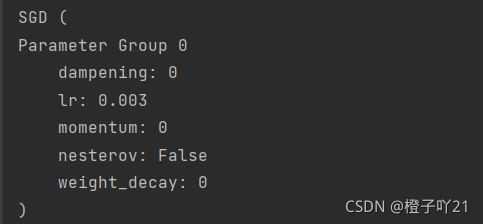
# 如果对某个参数不指定学习率，就使⽤最外层的默认学习率
# 调整学习率
for param_group in optimizer.param_groups:
 param_group['lr'] *= 0.1 # 学习率为之前的0.1倍
print(optimizer)

 

8、训练模型 通过调⽤ optim 实例的 step 函数来迭代模型参数。

num_epochs = 3 #做三次循环
for epoch in range(1, num_epochs + 1): #循环函数
    for X, y in data_iter:  #一次一次的把小批量拿出来
        output = net(X) #输出到net里面
        l = loss(output, y.view(-1, 1))
        optimizer.zero_grad() # 梯度清零，等价于net.zero_grad()
        l.backward() #计算梯度
        optimizer.step() #调用step函数进行模型更新
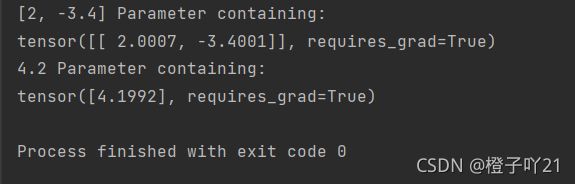
    print('epoch %d, loss: %f' % (epoch, l.item()))

⽐较学到的模型参数和真实的模型参数。我们从 net 获得需要的层，并访问其权᯿（ weight ）和偏差（ bias ）

dense = net[0]
print(true_w, dense.weight)
print(true_b, dense.bias)