从FM推演各深度学习CTR预估模型(附代码)
作者: 龙心尘 && 寒小阳
时间:2018年7月
出处:https://blog.csdn.net/longxinchen_ml/article/details/81031736
https://blog.csdn.net/han_xiaoyang/article/details/81031961
声明:版权所有,转载请联系作者并注明出处。本文代码部分参考了lambda等同学的tensorflow实现,在此向原作者表示感谢。
注:本文根据作者在公司内训讲稿整理而成。
多年以后,当资深算法专家们看着无缝对接用户需求的广告收入节节攀升时,他们可能会想起自己之前痛苦推导FM与深度学习公式的某个夜晚……——题记
1.引言
**点击率(click-through rate, CTR)**是互联网公司进行流量分配的核心依据之一。比如互联网广告平台,为了精细化权衡和保障用户、广告、平台三方的利益,准确的CTR预估是不可或缺的。CTR预估技术从传统的逻辑回归,到近两年大火的深度学习,新的算法层出不穷:DeepFM, NFM, DIN, AFM, DCN……
然而,相关的综述文章不少,但碎片罗列的居多,模型之间内在的联系和演化思路如何揭示?怎样才能迅速get到新模型的创新点和适用场景,快速提高新论文速度,节约理解、复现模型的成本?这些都是亟待解决的问题。
我们认为,从FM及其与神经网络的结合出发,能够迅速贯穿很多深度学习CTR预估网络的思路,从而更好地理解和应用模型。
2.本文的思路与方法
- 我们试图从原理上进行推导、理解各个深度CTR预估模型之间的相互关系,知其然也知其所以然。(以下的分析与拆解角度,是一种我们尝试的理解视角,并不是唯一的理解方式)
- 推演的核心思路:“通过设计网络结构进行组合特征的挖掘”。
- 具体来说有两条:其一是从FM开始推演其在深度学习上的各种推广(对应下图的红线),另一条是从embedding+MLP自身的演进特点结合CTR预估本身的业务场景进行推演(对应下图黑线部分)。
![]()
- 为了便于理解,我们简化了数据案例——只考虑离散特征数据的建模,以分析不同神经网络在处理相同业务问题时的不同思路。
- 同时,我们将各典型论文不同风格的神经网络结构图统一按照计算图来绘制,以便于对比不同模型。
3.FM:降维版本的特征二阶组合
CTR预估本质是一个二分类问题,以移动端展示广告推荐为例,依据日志中的用户侧的信息(比如年龄,性别,国籍,手机上安装的app列表)、广告侧的信息(广告id,广告类别,广告标题等)、上下文侧信息(渠道id等),去建模预测用户是否会点击该广告。
FM出现之前的传统的处理方法是人工特征工程加上线性模型(如逻辑回归Logistic Regression)。为了提高模型效果,关键技术是找到到用户点击行为背后隐含的特征组合。如男性、大学生用户往往会点击游戏类广告,因此**“男性且是大学生且是游戏类”**的特征组合就是一个关键特征。但这本质仍是线性模型,其假设函数表示成内积形式一般为:
y l i n e a r = σ ( ⟨ w ⃗ , x ⃗ ⟩ ) y _ { linear } = \sigma \left( \langle \vec { w } , \vec { x } \rangle \right) ylinear=σ(⟨w,x⟩)
其中 x ⃗ \vec{x} x为特征向量, w ⃗ \vec{w} w为权重向量, σ ( ) σ() σ()为sigmoid函数。
但是人工进行特征组合通常会存在诸多困难,如特征爆炸、特征难以被识别、组合特征难以设计等。为了让模型自动地考虑特征之间的二阶组合信息,线性模型推广为二阶多项式( 2 d − P o l y n o m i a l 2d-Polynomial 2d−Polynomial)模型:
y p o l y = σ ( ⟨ w ⃗ , x ⃗ ⟩ + ∑ i = 1 n ∑ j = 1 n w i j ⋅ x i ⋅ x j ) y _ { p o l y } = \sigma \left( \langle \vec { w } , \vec { x } \rangle + \sum _ { i = 1 } ^ { n } \sum _ { j = 1 } ^ { n } w _ { i j } \cdot x _ { i } \cdot x _ { j } \right) ypoly=σ(⟨w,x⟩+i=1∑nj=1∑nwij⋅xi⋅xj)
其实就是对特征两两相乘(组合)构成新特征(离散化之后其实就是“且”操作),并对每个新特征分配独立的权重,通过机器学习来自动得到这些权重。将其写成矩阵形式为:
y p o l y = σ ( w ⃗ T ⋅ x ⃗ + x ⃗ T ⋅ W ( 2 ) ⋅ x ⃗ ) y _ { p o l y } = \sigma \left( \vec { w } ^ { T } \cdot \vec { x } + \vec { x } ^ { T } \cdot W ^ { ( 2 ) } \cdot \vec { x } \right) ypoly=σ(wT⋅x+xT⋅W(2)⋅x)
其中 W ( 2 ) W^{(2)} W(2)为二阶特征组合的权重矩阵,是对称矩阵。而这个矩阵参数非常多,为 O ( n 2 ) O(n^2) O(n2)。为了降低该矩阵的维度,可以将其因子分解( F a c t o r i z a t i o n Factorization Factorization)为两个低维(比如 n ∗ k n*k n∗k)矩阵的相乘。则此时 W W W矩阵的参数就大幅降低,为 O ( n k ) O(nk) O(nk)。公式如下:
W ( 2 ) = W T ⋅ W W ^ { ( 2 ) } = W ^ { T } \cdot W W(2)=WT⋅W
这就是 R e n d l e Rendle Rendle等在2010年提出因子分解机(Factorization Machines,FM)的名字的由来。FM的矩阵形式公式如下:
y F M = σ ( w ⃗ T ⋅ x ⃗ + x ⃗ T ⋅ W T ⋅ W ⋅ x ⃗ ) y _ { F M } = \sigma \left( \vec { w } ^ { T } \cdot \vec { x } + \vec { x } ^ { T } \cdot W ^ { T } \cdot W \cdot \vec { x } \right) yFM=σ(wT⋅x+xT⋅WT⋅W⋅x)
将其写成内积的形式:
y F M = σ ( ⟨ w ⃗ , x ⃗ ⟩ + ⟨ W ⋅ x ⃗ , W ⋅ x ⃗ ⟩ ) y _ { F M } = \sigma ( \langle \vec { w } , \vec { x } \rangle + \langle W \cdot \vec { x } , W \cdot \vec { x } \rangle ) yFM=σ(⟨w,x⟩+⟨W⋅x,W⋅x⟩)
利用$ \langle \sum_{i=1}^n \vec{a_i},\sum_{i=1}^n \vec{a_i}\rangle= \sum_{i=1}n\sum_{j=1}n \langle \vec{a_i}, \vec{a_j}\rangle $,可以将上式进一步改写成求和式的形式:
y F M = σ ( ⟨ w ⃗ , x ⃗ ⟩ + ∑ i = 1 n ∑ j = 1 n ⟨ x i ⋅ v ⃗ i , x j ⋅ v ⃗ j ⟩ ) y _ { F M } = \sigma \left( \langle \vec { w } , \vec { x } \rangle + \sum _ { i = 1 } ^ { n } \sum _ { j = 1 } ^ { n } \left\langle x _ { i } \cdot \vec { v } _ { i } , x _ { j } \cdot \vec { v } _ { j } \right\rangle \right) yFM=σ(⟨w,x⟩+i=1∑nj=1∑n⟨xi⋅vi,xj⋅vj⟩)
其中 v i ⃗ \vec{v_i} vi向量是矩阵 W W W的第 i i i列。为了去除重复项与特征平方项,上式可以进一步改写成更为常见的FM公式:
y F M = σ ( ⟨ w ⃗ , x ⃗ ⟩ + ∑ i = 1 n ∑ j = i + 1 n ⟨ v ⃗ i , v ⃗ j ⟩ x i ⋅ x j ) y _ { F M } = \sigma \left( \langle \vec { w } , \vec { x } \rangle + \sum _ { i = 1 } ^ { n } \sum _ { j = i + 1 } ^ { n } \left\langle \vec { v } _ { i } , \vec { v } _ { j } \right\rangle x _ { i } \cdot x _ { j } \right) yFM=σ(⟨w,x⟩+i=1∑nj=i+1∑n⟨vi,vj⟩xi⋅xj)
对比二阶多项式模型,FM模型中特征两两相乘(组合)的权重是相互不独立的,它是一种参数较少但表达力强的模型。
此处附上FM的TensorFlow代码实现,完整数据和代码请参考网盘。注意FM通过内积进行无重复项与特征平方项的特征组合过程使用了一个小trick,就是:
∑ i = 1 n ∑ j = i + 1 n x i x j = 1 / 2 × [ ( ∑ i = 1 n x i ) 2 − ∑ i = 1 n x i 2 ] \sum_{i=1}^n\sum_{j=i+1}^n x_ix_j = 1/2 × [(\sum_{i=1}^n x_i)^2 - \sum_{i=1}^n x_i^2] i=1∑nj=i+1∑nxixj=1/2×[(i=1∑nxi)2−i=1∑nxi2]
class FM(Model):
def __init__(self, input_dim=None, output_dim=1, factor_order=10, init_path=None, opt_algo='gd', learning_rate=1e-2,
l2_w=0, l2_v=0, random_seed=None):
Model.__init__(self)
# 一次、二次交叉、偏置项
init_vars = [('w', [input_dim, output_dim], 'xavier', dtype),
('v', [input_dim, factor_order], 'xavier', dtype),
('b', [output_dim], 'zero', dtype)]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = tf.sparse_placeholder(dtype)
self.y = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w = self.vars['w']
v = self.vars['v']
b = self.vars['b']
# [(x1+x2+x3)^2 - (x1^2+x2^2+x3^2)]/2
# 先计算所有的交叉项,再减去平方项(自己和自己相乘)
X_square = tf.SparseTensor(self.X.indices, tf.square(self.X.values), tf.to_int64(tf.shape(self.X)))
xv = tf.square(tf.sparse_tensor_dense_matmul(self.X, v))
p = 0.5 * tf.reshape(
tf.reduce_sum(xv - tf.sparse_tensor_dense_matmul(X_square, tf.square(v)), 1),
[-1, output_dim])
xw = tf.sparse_tensor_dense_matmul(self.X, w)
logits = tf.reshape(xw + b + p, [-1])
self.y_prob = tf.sigmoid(logits)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=self.y)) + \
l2_w * tf.nn.l2_loss(xw) + \
l2_v * tf.nn.l2_loss(xv)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
#GPU设定
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
# 图中所有variable初始化
tf.global_variables_initializer().run(session=self.sess)
4.用神经网络的视角看FM:嵌入后再进行内积
我们观察FM公式的矩阵内积形式:
y F M = σ ( ⟨ w ⃗ , x ⃗ ⟩ + ⟨ W ⋅ x ⃗ , W ⋅ x ⃗ ⟩ ) y _ { F M } = \sigma ( \langle \vec { w } , \vec { x } \rangle + \langle W \cdot \vec { x } , W \cdot \vec { x } \rangle ) yFM=σ(⟨w,x⟩+⟨W⋅x,W⋅x⟩)
发现 W ⋅ x ⃗ W·\vec{x} W⋅x部分就是将离散系数特征通过矩阵乘法降维成一个低维稠密向量。这个过程对神经网络来说就叫做嵌入(embedding)。所以用神经网络视角来看:
- FM首先是对离散特征进行嵌入。
- 之后通过对嵌入后的稠密向量进行内积来进行二阶特征组合。
- 最后再与线性模型的结果求和进而得到预估点击率。
其示意图如下。为了表述清晰,我们绘制的是神经网络计算图而不是网络结构图——在网络结构图中增加了权重 W W W的位置。
![]()
5.FM的实际应用:考虑领域信息
广告点击率预估模型中的特征以分领域的离散特征为主,如:广告类别、用户职业、手机APP列表等。由于连续特征比较好处理,为了简化起见,本文只考虑同时存在不同领域的离散特征的情形。处理离散特征的常见方法是通过独热(one-hot)编码转换为一系列二值特征向量。然后将这些高维稀疏特征通过嵌入(embedding)转换为低维连续特征。前面已经说明FM中间的一个核心步骤就是嵌入,但这个嵌入过程没有考虑领域信息。这使得同领域内的特征也被当做不同领域特征进行两两组合了。
其实可以将特征具有领域关系的特点作为先验知识加入到神经网络的设计中去:同领域的特征嵌入后直接求和作为一个整体嵌入向量,进而与其他领域的整体嵌入向量进行两两组合。而这个先嵌入后求和的过程,就是一个单领域的小离散特征向量乘以矩阵的过程。此时FM的过程变为:对不同领域的离散特征分别进行嵌入,之后再进行二阶特征的向量内积。其计算图图如下所示:
![]()
这样考虑其实是给FM增加了一个正则:考虑了领域内的信息的相似性。而且还有一个附加的好处,这些嵌入后的同领域特征可以拼接起来作为更深的神经网络的输入,达到降维的目的。接下来我们将反复看到这种处理方式。
此处需要注意,这与“基于领域的因子分解机”(Field-aware Factorization Machines,FFM)有区别。FFM也是FM的另一种变体,也考虑了领域信息。但其不同点是同一个特征与不同领域进行特征组合时,其对应的嵌入向量是不同的。本文不考虑FFM的作用机制。
经过这些改进的FM终究还是浅层网络,它的表现力仍然有限。为了增加模型的表现力(model capacity),一个自然的想法就是将该浅层网络不断“深化”。
6.embedding+MLP:深度学习CTR预估的通用框架
embedding+MLP是对于分领域离散特征进行深度学习CTR预估的通用框架。深度学习在特征组合挖掘(特征学习)方面具有很大的优势。比如以CNN为代表的深度网络主要用于图像、语音等稠密特征上的学习,以W2V、RNN为代表的深度网络主要用于文本的同质化、序列化高维稀疏特征的学习。CTR预估的主要场景是对离散且有具体领域的特征进行学习,所以其深度网络结构也不同于CNN与RNN。
具体来说, embedding+MLP的过程如下:
- 对不同领域的one-hot特征进行嵌入(embedding),使其降维成低维度稠密特征。
- 然后将这些特征向量拼接(concatenate)成一个隐含层。
- 之后再不断堆叠全连接层,也就是多层感知机(Multilayer Perceptron, MLP,有时也叫作前馈神经网络)。
- 最终输出预测的点击率。
其示意图如下:
![]()
embedding+MLP的缺点是只学习高阶特征组合,对于低阶或者手动的特征组合不够兼容,而且参数较多,学习较困难。
7.FNN:FM与MLP的串联结合
Weinan Zhang等在2016年提出的因子分解机神经网络(Factorisation Machine supported Neural Network,FNN)将考FM与MLP进行了结合。它有着十分显著的特点:
- 采用FM预训练得到的隐含层及其权重作为神经网络的第一层的初始值,之后再不断堆叠全连接层,最终输出预测的点击率。
- 可以将FNN理解成一种特殊的embedding+MLP,其要求第一层嵌入后的各领域特征维度一致,并且嵌入权重的初始化是FM预训练好的。
- 这不是一个端到端的训练过程,有贪心训练的思路。而且如果不考虑预训练过程,模型网络结构也没有考虑低阶特征组合。
其计算图如下所示:
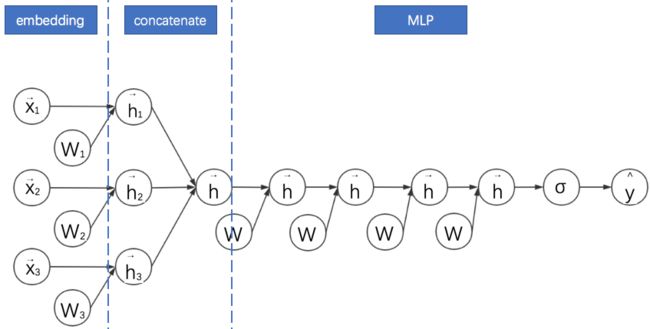
通过观察FFN的计算图可以看出其与embedding+MLP确实非常像。**不过此处省略了FNN的FM部分的线性模块。**这种省略为了更好地进行两个模型的对比。接下来的计算图我们都会省略线性模块。
此处附上FNN的代码实现,完整数据和代码请参考网盘。:
class FNN(Model):
def __init__(self, field_sizes=None, embed_size=10, layer_sizes=None, layer_acts=None, drop_out=None,
embed_l2=None, layer_l2=None, init_path=None, opt_algo='gd', learning_rate=1e-2, random_seed=None):
Model.__init__(self)
init_vars = []
num_inputs = len(field_sizes)
for i in range(num_inputs):
init_vars.append(('embed_%d' % i, [field_sizes[i], embed_size], 'xavier', dtype))
node_in = num_inputs * embed_size
for i in range(len(layer_sizes)):
init_vars.append(('w%d' % i, [node_in, layer_sizes[i]], 'xavier', dtype))
init_vars.append(('b%d' % i, [layer_sizes[i]], 'zero', dtype))
node_in = layer_sizes[i]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = [tf.sparse_placeholder(dtype) for i in range(num_inputs)]
self.y = tf.placeholder(dtype)
self.keep_prob_train = 1 - np.array(drop_out)
self.keep_prob_test = np.ones_like(drop_out)
self.layer_keeps = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w0 = [self.vars['embed_%d' % i] for i in range(num_inputs)]
xw = tf.concat([tf.sparse_tensor_dense_matmul(self.X[i], w0[i]) for i in range(num_inputs)], 1)
l = xw
#全连接部分
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
bi = self.vars['b%d' % i]
print(l.shape, wi.shape, bi.shape)
l = tf.nn.dropout(
activate(
tf.matmul(l, wi) + bi,
layer_acts[i]),
self.layer_keeps[i])
l = tf.squeeze(l)
self.y_prob = tf.sigmoid(l)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=l, labels=self.y))
if layer_l2 is not None:
self.loss += embed_l2 * tf.nn.l2_loss(xw)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
self.loss += layer_l2[i] * tf.nn.l2_loss(wi)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
tf.global_variables_initializer().run(session=self.sess)
8.DeepFM: FM与MLP的并联结合
针对FNN需要预训练的问题,Huifeng Guo等提出了深度因子分解机模型(Deep Factorisation Machine, DeepFM, 2017)。该模型的特点是:
- 不需要预训练。
- 将考虑领域信息的FM部分与MLP部分并联起来(借用初中电路的术语),其实就是对两个模型进行联合训练。
- 考虑领域信息的FM部分的嵌入向量拼接起来作为MLP部分的输入特征,也就是是两个模型共享嵌入后的特征。
其计算图如下所示:
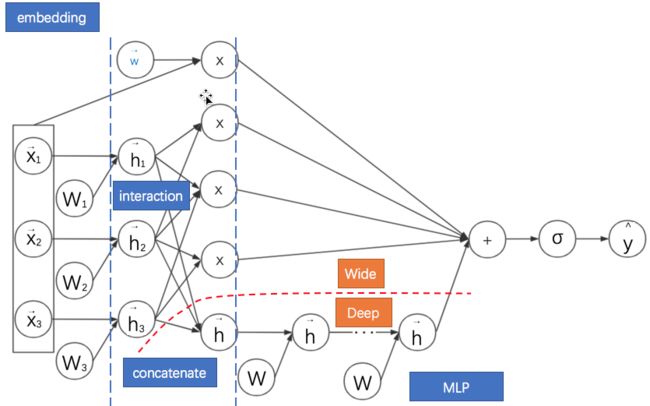
通过观察DeepFM的计算图可以看出红色虚线以上部分其实就是FM部分,虚线以下就是MLP部分。
此处附上DeepFM的代码实现,完整数据和代码请参考网盘。:
def model_fn(features, labels, mode, params):
"""Bulid Model function f(x) for Estimator."""
#------超参数的设定----
field_size = params["field_size"]
feature_size = params["feature_size"]
embedding_size = params["embedding_size"]
l2_reg = params["l2_reg"]
learning_rate = params["learning_rate"]
#batch_norm_decay = params["batch_norm_decay"]
#optimizer = params["optimizer"]
layers = map(int, params["deep_layers"].split(','))
dropout = map(float, params["dropout"].split(','))
#------权重------
FM_B = tf.get_variable(name='fm_bias', shape=[1], initializer=tf.constant_initializer(0.0))
FM_W = tf.get_variable(name='fm_w', shape=[feature_size], initializer=tf.glorot_normal_initializer())
# F
FM_V = tf.get_variable(name='fm_v', shape=[feature_size, embedding_size], initializer=tf.glorot_normal_initializer())
# F * E
#------build feaure-------
feat_ids = features['feat_ids']
feat_ids = tf.reshape(feat_ids,shape=[-1,field_size]) # None * f/K * K
feat_vals = features['feat_vals']
feat_vals = tf.reshape(feat_vals,shape=[-1,field_size]) # None * f/K * K
#------build f(x)------
with tf.variable_scope("First-order"):
feat_wgts = tf.nn.embedding_lookup(FM_W, feat_ids) # None * f/K * K
y_w = tf.reduce_sum(tf.multiply(feat_wgts, feat_vals),1)
with tf.variable_scope("Second-order"):
embeddings = tf.nn.embedding_lookup(FM_V, feat_ids) # None * f/K * K * E
feat_vals = tf.reshape(feat_vals, shape=[-1, field_size, 1]) # None * f/K * K * 1 ?
embeddings = tf.multiply(embeddings, feat_vals) #vij*xi
sum_square = tf.square(tf.reduce_sum(embeddings,1)) # None * K * E
square_sum = tf.reduce_sum(tf.square(embeddings),1)
y_v = 0.5*tf.reduce_sum(tf.subtract(sum_square, square_sum),1) # None * 1
with tf.variable_scope("Deep-part"):
if FLAGS.batch_norm:
#normalizer_fn = tf.contrib.layers.batch_norm
#normalizer_fn = tf.layers.batch_normalization
if mode == tf.estimator.ModeKeys.TRAIN:
train_phase = True
#normalizer_params = {'decay': batch_norm_decay, 'center': True, 'scale': True, 'updates_collections': None, 'is_training': True, 'reuse': None}
else:
train_phase = False
#normalizer_params = {'decay': batch_norm_decay, 'center': True, 'scale': True, 'updates_collections': None, 'is_training': False, 'reuse': True}
else:
normalizer_fn = None
normalizer_params = None
deep_inputs = tf.reshape(embeddings,shape=[-1,field_size*embedding_size]) # None * (F*K)
for i in range(len(layers)):
#if FLAGS.batch_norm:
# deep_inputs = batch_norm_layer(deep_inputs, train_phase=train_phase, scope_bn='bn_%d' %i)
#normalizer_params.update({'scope': 'bn_%d' %i})
deep_inputs = tf.contrib.layers.fully_connected(inputs=deep_inputs, num_outputs=layers[i], \
#normalizer_fn=normalizer_fn, normalizer_params=normalizer_params, \
weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg), scope='mlp%d' % i)
if FLAGS.batch_norm:
deep_inputs = batch_norm_layer(deep_inputs, train_phase=train_phase, scope_bn='bn_%d' %i) #放在RELU之后 https://github.com/ducha-aiki/caffenet-benchmark/blob/master/batchnorm.md#bn----before-or-after-relu
if mode == tf.estimator.ModeKeys.TRAIN:
deep_inputs = tf.nn.dropout(deep_inputs, keep_prob=dropout[i]) #Apply Dropout after all BN layers and set dropout=0.8(drop_ratio=0.2)
#deep_inputs = tf.layers.dropout(inputs=deep_inputs, rate=dropout[i], training=mode == tf.estimator.ModeKeys.TRAIN)
y_deep = tf.contrib.layers.fully_connected(inputs=deep_inputs, num_outputs=1, activation_fn=tf.identity, \
weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg), scope='deep_out')
y_d = tf.reshape(y_deep,shape=[-1])
#sig_wgts = tf.get_variable(name='sigmoid_weights', shape=[layers[-1]], initializer=tf.glorot_normal_initializer())
#sig_bias = tf.get_variable(name='sigmoid_bias', shape=[1], initializer=tf.constant_initializer(0.0))
#deep_out = tf.nn.xw_plus_b(deep_inputs,sig_wgts,sig_bias,name='deep_out')
with tf.variable_scope("DeepFM-out"):
#y_bias = FM_B * tf.ones_like(labels, dtype=tf.float32) # None * 1 warning;这里不能用label,否则调用predict/export函数会出错,train/evaluate正常;初步判断estimator做了优化,用不到label时不传
y_bias = FM_B * tf.ones_like(y_d, dtype=tf.float32) # None * 1
y = y_bias + y_w + y_v + y_d
pred = tf.sigmoid(y)
predictions={
"prob": pred}
export_outputs = {
tf.saved_model.signature_constants.DEFAULT_SERVING_SIGNATURE_DEF_KEY: tf.estimator.export.PredictOutput(predictions)}
# Provide an estimator spec for `ModeKeys.PREDICT`
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
export_outputs=export_outputs)
#------bulid loss------
loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=y, labels=labels)) + \
l2_reg * tf.nn.l2_loss(FM_W) + \
l2_reg * tf.nn.l2_loss(FM_V) #+ \ l2_reg * tf.nn.l2_loss(sig_wgts)
# Provide an estimator spec for `ModeKeys.EVAL`
eval_metric_ops = {
"auc": tf.metrics.auc(labels, pred)
}
if mode == tf.estimator.ModeKeys.EVAL:
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
loss=loss,
eval_metric_ops=eval_metric_ops)
#------bulid optimizer------
if FLAGS.optimizer == 'Adam':
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate, beta1=0.9, beta2=0.999, epsilon=1e-8)
elif FLAGS.optimizer == 'Adagrad':
optimizer = tf.train.AdagradOptimizer(learning_rate=learning_rate, initial_accumulator_value=1e-8)
elif FLAGS.optimizer == 'Momentum':
optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=0.95)
elif FLAGS.optimizer == 'ftrl':
optimizer = tf.train.FtrlOptimizer(learning_rate)
train_op = optimizer.minimize(loss, global_step=tf.train.get_global_step())
# Provide an estimator spec for `ModeKeys.TRAIN` modes
if mode == tf.estimator.ModeKeys.TRAIN:
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
loss=loss,
train_op=train_op)
9.NFM:通过逐元素乘法延迟FM的实现过程
我们再回到考虑领域信息的FM,它仍有改进的空间。因为以上这些网络的FM部分都是只进行嵌入向量的两两内积后直接求和,没有充分利用二阶特征组合的信息。Xiangnan He等在2017年提出了神经网络因子分解机(Neural Factorization Machines,NFM)对此作出了改进。其计算图如下所示:
![]()
NFM的基本特点是:
- 利用二阶交互池化层(Bi-Interaction Pooling)对FM嵌入后的向量两两进行元素级别的乘法,形成同维度的向量求和后作为前馈神经网络的输入。计算图中用圈乘 ⨂ \bigotimes ⨂表示逐元素乘法运算。
- NFM与DeepFM的区别是没有单独的FM的浅层网络进行联合训练,而是将其整合后直接输出给前馈神经网络。
- 当MLP的全连接层都是恒等变换且最后一层参数全为1时,NFM就退化成了FM。可见,NFM是FM的推广,它推迟了FM的实现过程,并在其中加入了更多非线性运算。
- 另一方面,我们观察计算图会发现NFM与FNN非常相似。它们的主要区别是NFM 在embedding之后对特征进行了两两逐元素乘法。因为逐元素相乘的向量维数不变,之后对这些向量求和的维数仍然与embedding的维数一致。因此输入到MLP的参数比起直接concatenate的FNN更少。
此处附上NFM的代码实现,完整数据和代码请参考网盘:
def model_fn(features, labels, mode, params):
"""Bulid Model function f(x) for Estimator."""
#------hyperparameters----
field_size = params["field_size"]
feature_size = params["feature_size"]
embedding_size = params["embedding_size"]
l2_reg = params["l2_reg"]
learning_rate = params["learning_rate"]
#optimizer = params["optimizer"]
layers = map(int, params["deep_layers"].split(','))
dropout = map(float, params["dropout"].split(','))
#------bulid weights------
Global_Bias = tf.get_variable(name='bias', shape=[1], initializer=tf.constant_initializer(0.0))
Feat_Bias = tf.get_variable(name='linear', shape=[feature_size], initializer=tf.glorot_normal_initializer())
Feat_Emb = tf.get_variable(name='emb', shape=[feature_size,embedding_size], initializer=tf.glorot_normal_initializer())
#------build feaure-------
feat_ids = features['feat_ids']
feat_ids = tf.reshape(feat_ids,shape=[-1,field_size])
feat_vals = features['feat_vals']
feat_vals = tf.reshape(feat_vals,shape=[-1,field_size])
#------build f(x)------
with tf.variable_scope("Linear-part"):
feat_wgts = tf.nn.embedding_lookup(Feat_Bias, feat_ids) # None * F * 1
y_linear = tf.reduce_sum(tf.multiply(feat_wgts, feat_vals),1)
with tf.variable_scope("BiInter-part"):
embeddings = tf.nn.embedding_lookup(Feat_Emb, feat_ids) # None * F * K
feat_vals = tf.reshape(feat_vals, shape=[-1, field_size, 1])
embeddings = tf.multiply(embeddings, feat_vals) # vij * xi
sum_square_emb = tf.square(tf.reduce_sum(embeddings,1))
square_sum_emb = tf.reduce_sum(tf.square(embeddings),1)
deep_inputs = 0.5*tf.subtract(sum_square_emb, square_sum_emb) # None * K
with tf.variable_scope("Deep-part"):
if mode == tf.estimator.ModeKeys.TRAIN:
train_phase = True
else:
train_phase = False
if mode == tf.estimator.ModeKeys.TRAIN:
deep_inputs = tf.nn.dropout(deep_inputs, keep_prob=dropout[0]) # None * K
for i in range(len(layers)):
deep_inputs = tf.contrib.layers.fully_connected(inputs=deep_inputs, num_outputs=layers[i], \
weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg), scope='mlp%d' % i)
if FLAGS.batch_norm:
deep_inputs = batch_norm_layer(deep_inputs, train_phase=train_phase, scope_bn='bn_%d' %i) #放在RELU之后 https://github.com/ducha-aiki/caffenet-benchmark/blob/master/batchnorm.md#bn----before-or-after-relu
if mode == tf.estimator.ModeKeys.TRAIN:
deep_inputs = tf.nn.dropout(deep_inputs, keep_prob=dropout[i]) #Apply Dropout after all BN layers and set dropout=0.8(drop_ratio=0.2)
#deep_inputs = tf.layers.dropout(inputs=deep_inputs, rate=dropout[i], training=mode == tf.estimator.ModeKeys.TRAIN)
y_deep = tf.contrib.layers.fully_connected(inputs=deep_inputs, num_outputs=1, activation_fn=tf.identity, \
weights_regularizer=tf.contrib.layers.l2_regularizer(l2_reg), scope='deep_out')
y_d = tf.reshape(y_deep,shape=[-1])
with tf.variable_scope("NFM-out"):
#y_bias = Global_Bias * tf.ones_like(labels, dtype=tf.float32) # None * 1 warning;这里不能用label,否则调用predict/export函数会出错,train/evaluate正常;初步判断estimator做了优化,用不到label时不传
y_bias = Global_Bias * tf.ones_like(y_d, dtype=tf.float32) # None * 1
y = y_bias + y_linear + y_d
pred = tf.sigmoid(y)
predictions={
"prob": pred}
export_outputs = {
tf.saved_model.signature_constants.DEFAULT_SERVING_SIGNATURE_DEF_KEY: tf.estimator.export.PredictOutput(predictions)}
# Provide an estimator spec for `ModeKeys.PREDICT`
if mode == tf.estimator.ModeKeys.PREDICT:
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
export_outputs=export_outputs)
#------bulid loss------
loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=y, labels=labels)) + \
l2_reg * tf.nn.l2_loss(Feat_Bias) + l2_reg * tf.nn.l2_loss(Feat_Emb)
# Provide an estimator spec for `ModeKeys.EVAL`
eval_metric_ops = {
"auc": tf.metrics.auc(labels, pred)
}
if mode == tf.estimator.ModeKeys.EVAL:
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
loss=loss,
eval_metric_ops=eval_metric_ops)
#------bulid optimizer------
if FLAGS.optimizer == 'Adam':
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate, beta1=0.9, beta2=0.999, epsilon=1e-8)
elif FLAGS.optimizer == 'Adagrad':
optimizer = tf.train.AdagradOptimizer(learning_rate=learning_rate, initial_accumulator_value=1e-8)
elif FLAGS.optimizer == 'Momentum':
optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=0.95)
elif FLAGS.optimizer == 'ftrl':
optimizer = tf.train.FtrlOptimizer(learning_rate)
train_op = optimizer.minimize(loss, global_step=tf.train.get_global_step())
# Provide an estimator spec for `ModeKeys.TRAIN` modes
if mode == tf.estimator.ModeKeys.TRAIN:
return tf.estimator.EstimatorSpec(
mode=mode,
predictions=predictions,
loss=loss,
train_op=train_op)
10.AFM: 对简化版NFM进行加权求和
NFM的主要创新点是在FM过程中添加了逐元素相乘的运算来增加模型的复杂度。但没有在此基础上添加更复杂的运算过程,比如对加权求和。Jun Xiao等在2017年提出了注意力因子分解模型(Attentional Factorization Machine,AFM)就是在这个方向上的改进。其计算图如下所示:
![]()
AFM的特点是:
- AFM与NFM都是致力于充分利用二阶特征组合的信息,对嵌入后的向量两两进行逐元素乘法,形成同维度的向量。而且AFM没有MLP部分。
- AFM通过在逐元素乘法之后形成的向量进行加权求和,而且权重是基于网络自身来产生的。其方法是引入一个注意力子网络(Attention Net)。
- 当权重都相等时,AFM退化成无全连接层的NFM。
- “注意力子网络”的主要操作是进行矩阵乘法,其最终输出结果为softmax,以保证各分量的权重本身是一个概率分布。
11.PNN:通过改进向量乘法运算延迟FM的实现过程
再回到FM。既然AFM、NFM可以通过添加逐元素乘法的运算来增加模型的复杂度,那向量乘法有这么多,可否用其他的方法增加FM复杂度?答案是可以的。Huifeng Guo等在2016年提出了基于向量积的神经网络(Product-based Neural Networks,PNN)就是一个典型例子。其简化计算图如下所示:
![]()
对比之前模型的计算图,我们可以发现PNN的基本特点是:
- 利用二阶向量积层(Pair-wisely Connected Product Layer)对FM嵌入后的向量两两进行向量积,形成的结果作为之后MLP的输入。计算图中用圆点•表示向量积运算。PNN采用的向量积有内积与外积两种形式。
- 需要说明的是,本计算图中省略了PNN中向量与常数1进行的乘法运算。这部分其实与FNN类似,不是PNN的主要创新点。故在此图中省略。
- 对于内积形式的PNN,因为两个向量相乘的结果为标量,可以直接把各个标量“拼接”成一个大向量,就可以作为MLP的输入了。
- 当MLP的全连接层都是恒等变换且最后一层参数全为1时,内积形式的PNN就退化成了FM。
- 对于外积形式的PNN,因为两个向量相乘相当于列向量与行向量进行矩阵相乘,得到的结果为一个矩阵。各个矩阵向之前内积形式的操作一样直接拼接起来维数太多,论文的简化方案是直接对各个矩阵进行求和,得到的新矩阵(可以理解成之后对其拉长成向量)就直接作为MLP的输入。
- 观察计算图发现外积形式的PNN与NFM很像,其实就是PNN把NFM的逐元素乘法换成了外积。
此处分别附上PNN的内积与外积形式代码,完整数据和代码请参考网盘。
class PNN1(Model):
def __init__(self, field_sizes=None, embed_size=10, layer_sizes=None, layer_acts=None, drop_out=None,
embed_l2=None, layer_l2=None, init_path=None, opt_algo='gd', learning_rate=1e-2, random_seed=None):
Model.__init__(self)
init_vars = []
num_inputs = len(field_sizes)
for i in range(num_inputs):
init_vars.append(('embed_%d' % i, [field_sizes[i], embed_size], 'xavier', dtype))
num_pairs = int(num_inputs * (num_inputs - 1) / 2)
node_in = num_inputs * embed_size + num_pairs
# node_in = num_inputs * (embed_size + num_inputs)
for i in range(len(layer_sizes)):
init_vars.append(('w%d' % i, [node_in, layer_sizes[i]], 'xavier', dtype))
init_vars.append(('b%d' % i, [layer_sizes[i]], 'zero', dtype))
node_in = layer_sizes[i]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = [tf.sparse_placeholder(dtype) for i in range(num_inputs)]
self.y = tf.placeholder(dtype)
self.keep_prob_train = 1 - np.array(drop_out)
self.keep_prob_test = np.ones_like(drop_out)
self.layer_keeps = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w0 = [self.vars['embed_%d' % i] for i in range(num_inputs)]
xw = tf.concat([tf.sparse_tensor_dense_matmul(self.X[i], w0[i]) for i in range(num_inputs)], 1)
xw3d = tf.reshape(xw, [-1, num_inputs, embed_size])
row = []
col = []
for i in range(num_inputs-1):
for j in range(i+1, num_inputs):
row.append(i)
col.append(j)
# batch * pair * k
p = tf.transpose(
# pair * batch * k
tf.gather(
# num * batch * k
tf.transpose(
xw3d, [1, 0, 2]),
row),
[1, 0, 2])
# batch * pair * k
q = tf.transpose(
tf.gather(
tf.transpose(
xw3d, [1, 0, 2]),
col),
[1, 0, 2])
p = tf.reshape(p, [-1, num_pairs, embed_size])
q = tf.reshape(q, [-1, num_pairs, embed_size])
ip = tf.reshape(tf.reduce_sum(p * q, [-1]), [-1, num_pairs])
# simple but redundant
# batch * n * 1 * k, batch * 1 * n * k
# ip = tf.reshape(
# tf.reduce_sum(
# tf.expand_dims(xw3d, 2) *
# tf.expand_dims(xw3d, 1),
# 3),
# [-1, num_inputs**2])
l = tf.concat([xw, ip], 1)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
bi = self.vars['b%d' % i]
l = tf.nn.dropout(
activate(
tf.matmul(l, wi) + bi,
layer_acts[i]),
self.layer_keeps[i])
l = tf.squeeze(l)
self.y_prob = tf.sigmoid(l)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=l, labels=self.y))
if layer_l2 is not None:
self.loss += embed_l2 * tf.nn.l2_loss(xw)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
self.loss += layer_l2[i] * tf.nn.l2_loss(wi)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
tf.global_variables_initializer().run(session=self.sess)
class PNN2(Model):
def __init__(self, field_sizes=None, embed_size=10, layer_sizes=None, layer_acts=None, drop_out=None,
embed_l2=None, layer_l2=None, init_path=None, opt_algo='gd', learning_rate=1e-2, random_seed=None,
layer_norm=True):
Model.__init__(self)
init_vars = []
num_inputs = len(field_sizes)
for i in range(num_inputs):
init_vars.append(('embed_%d' % i, [field_sizes[i], embed_size], 'xavier', dtype))
num_pairs = int(num_inputs * (num_inputs - 1) / 2)
node_in = num_inputs * embed_size + num_pairs
init_vars.append(('kernel', [embed_size, num_pairs, embed_size], 'xavier', dtype))
for i in range(len(layer_sizes)):
init_vars.append(('w%d' % i, [node_in, layer_sizes[i]], 'xavier', dtype))
init_vars.append(('b%d' % i, [layer_sizes[i]], 'zero', dtype))
node_in = layer_sizes[i]
self.graph = tf.Graph()
with self.graph.as_default():
if random_seed is not None:
tf.set_random_seed(random_seed)
self.X = [tf.sparse_placeholder(dtype) for i in range(num_inputs)]
self.y = tf.placeholder(dtype)
self.keep_prob_train = 1 - np.array(drop_out)
self.keep_prob_test = np.ones_like(drop_out)
self.layer_keeps = tf.placeholder(dtype)
self.vars = init_var_map(init_vars, init_path)
w0 = [self.vars['embed_%d' % i] for i in range(num_inputs)]
xw = tf.concat([tf.sparse_tensor_dense_matmul(self.X[i], w0[i]) for i in range(num_inputs)], 1)
xw3d = tf.reshape(xw, [-1, num_inputs, embed_size])
row = []
col = []
for i in range(num_inputs - 1):
for j in range(i + 1, num_inputs):
row.append(i)
col.append(j)
# batch * pair * k
p = tf.transpose(
# pair * batch * k
tf.gather(
# num * batch * k
tf.transpose(
xw3d, [1, 0, 2]),
row),
[1, 0, 2])
# batch * pair * k
q = tf.transpose(
tf.gather(
tf.transpose(
xw3d, [1, 0, 2]),
col),
[1, 0, 2])
# b * p * k
p = tf.reshape(p, [-1, num_pairs, embed_size])
# b * p * k
q = tf.reshape(q, [-1, num_pairs, embed_size])
# k * p * k
k = self.vars['kernel']
# batch * 1 * pair * k
p = tf.expand_dims(p, 1)
# batch * pair
kp = tf.reduce_sum(
# batch * pair * k
tf.multiply(
# batch * pair * k
tf.transpose(
# batch * k * pair
tf.reduce_sum(
# batch * k * pair * k
tf.multiply(
p, k),
-1),
[0, 2, 1]),
q),
-1)
#
# if layer_norm:
# # x_mean, x_var = tf.nn.moments(xw, [1], keep_dims=True)
# # xw = (xw - x_mean) / tf.sqrt(x_var)
# # x_g = tf.Variable(tf.ones([num_inputs * embed_size]), name='x_g')
# # x_b = tf.Variable(tf.zeros([num_inputs * embed_size]), name='x_b')
# # x_g = tf.Print(x_g, [x_g[:10], x_b])
# # xw = xw * x_g + x_b
# p_mean, p_var = tf.nn.moments(op, [1], keep_dims=True)
# op = (op - p_mean) / tf.sqrt(p_var)
# p_g = tf.Variable(tf.ones([embed_size**2]), name='p_g')
# p_b = tf.Variable(tf.zeros([embed_size**2]), name='p_b')
# # p_g = tf.Print(p_g, [p_g[:10], p_b])
# op = op * p_g + p_b
l = tf.concat([xw, kp], 1)
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
bi = self.vars['b%d' % i]
l = tf.nn.dropout(
activate(
tf.matmul(l, wi) + bi,
layer_acts[i]),
self.layer_keeps[i])
l = tf.squeeze(l)
self.y_prob = tf.sigmoid(l)
self.loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=l, labels=self.y))
if layer_l2 is not None:
self.loss += embed_l2 * tf.nn.l2_loss(xw)#tf.concat(w0, 0))
for i in range(len(layer_sizes)):
wi = self.vars['w%d' % i]
self.loss += layer_l2[i] * tf.nn.l2_loss(wi)
self.optimizer = get_optimizer(opt_algo, learning_rate, self.loss)
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
self.sess = tf.Session(config=config)
tf.global_variables_initializer().run(session=self.sess)
12.DCN:高阶FM的降维实现
以上的FM推广形式,主要是对FM进行二阶特征组合。高阶特征组合是通过MLP实现的。但这两种实现方式是有很大不同的,**FM更多是通过向量embedding之间的内积来实现,而MLP则是在向量embedding之后一层一层进行权重矩阵乘法实现。**可否直接将FM的过程在高阶特征组合上进行推广?答案是可以的。Ruoxi Wang等在2017提出的深度与交叉神经网络(Deep & Cross Network,DCN)就是在这个方向进行改进的。DCN的计算图如下:
![]()
DCN的特点如下:
- Deep部分就是普通的MLP网络,主要是全连接。
- 与DeepFM类似,DCN是由embedding+MLP部分与cross部分进行联合训练的。Cross部分是对FM部分的推广。
- cross部分的公式如下:
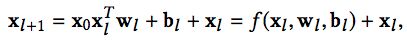
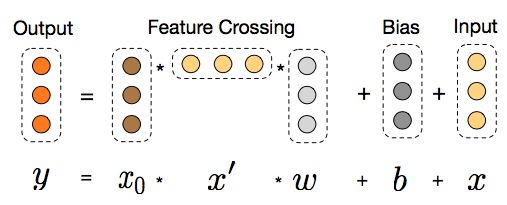
- 可以证明,cross网络是FM的过程在高阶特征组合的推广。完全的证明需要一些公式推导,感兴趣的同学可以直接参考原论文的附录。
- 而用简单的公式证明可以得到一个很重要的结论:只有两层且第一层与最后一层权重参数相等时的Cross网络与简化版FM等价。
- 此处对应简化版的FM视角是将拼接好的稠密向量作为输入向量,且不做领域方面的区分(但产生这些稠密向量的过程是考虑领域信息的,相对全特征维度的全连接层减少了大量参数,可以视作稀疏链接思想的体现)。而且之后进行embedding权重矩阵W只有一列——是退化成列向量的情形。
- 与MLP网络相比,Cross部分在增加高阶特征组合的同时减少了参数的个数,并省去了非线性激活函数。
13.Wide&Deep: DeepFM与DCN的基础框架
开篇已经提到,本文思路有两条主线。到此为止已经将基于FM的主线介绍基本完毕。接下来将串讲从embedding+MLP自身的演进特点的CTR预估模型主线,而这条思路与我们之前的FM思路同样有千丝万缕的联系。
Google在2016年提出的宽度与深度模型(Wide&Deep)在深度学习CTR预估模型中占有非常重要的位置,它奠定了之后基于深度学习的广告点击率预估模型的框架。
Wide&Deep将深度模型与线性模型进行联合训练,二者的结果求和输出为最终点击率。其计算图如下:
![]()
我们将Wide&Deep的计算图与之前的模型进行对比可知:
- Wide&Deep是前面介绍模型DeepFM与DCN的基础框架。这些模型均采用神经网络联合训练的思路,对神经网络进行并联。
- DeepFM、DCN与Wide&Deep的Deep部分都是MLP。
- Wide&Deep的Wide部分是逻辑回归,可以手动设计组合特征。
- DeepFM的Wide部分是FM,DCN的Wide部分是Cross网络,二者均不强求手动设计特征。但此时都与字面意义上的Wide有一定差异,因为均共享了降维后的嵌入特征。
此处附上DeepFM的代码实现,完整数据和代码请参考网盘:
def get_model(model_type, model_dir):
print("Model directory = %s" % model_dir)
# 对checkpoint去做设定
runconfig = tf.contrib.learn.RunConfig(
save_checkpoints_secs=None,
save_checkpoints_steps = 100,
)
m = None
# 宽模型
if model_type == 'WIDE':
m = tf.contrib.learn.LinearClassifier(
model_dir=model_dir,
feature_columns=wide_columns)
# 深度模型
if model_type == 'DEEP':
m = tf.contrib.learn.DNNClassifier(
model_dir=model_dir,
feature_columns=deep_columns,
hidden_units=[100, 50, 25])
# 宽度深度模型
if model_type == 'WIDE_AND_DEEP':
m = tf.contrib.learn.DNNLinearCombinedClassifier(
model_dir=model_dir,
linear_feature_columns=wide_columns,
dnn_feature_columns=deep_columns,
dnn_hidden_units=[100, 70, 50, 25],
config=runconfig)
print('estimator built')
return m
14.Deep Cross: DCN由其残差网络思想进化
由K. He等提出的深度残差网络能够大大加深神经网络的深度,同时不会引起退化的问题,显著提高了模型的精度。Ying Shan等将该思路应用到广告点击率预估模型中,提出深度交叉模型( D e e p C r o s s , 2016 Deep Cross, 2016 DeepCross,2016)。Deep Cross的计算图如下:
![]()
将Deep Cross与之前的模型对比,可以发现其特点是:
- 对embedding+MLP的改进主要是MLP部分增加跳跃连接成为残差网络。
- Deep Cross 与传统的残差网络的区别主要是没有采用卷积操作。其中一个原因是在广告点击率预估领域,特征不具备平移不变性。
- DCN其实是从Deep Cross进化出来的版本。DCN相对Deep Cross的主要贡献是解耦了Deep 与Cross(特征交叉)部分。
- 因此DCN中的Cross部分可以理解为残差网络的变体:其将Deep Cross的跨越链接缩短为只有一层,而全连接部分改为与权重向量和输入向量的内积。
15.DIN:对同领域历史信息引入注意力机制的MLP
以上神经网络对同领域离散特征的处理基本是将其嵌入后直接求和,这在一般情况下没太大问题。但其实可以做得更加精细。比如对于历史统计类特征。以用户历史浏览的商户id为例,假设用户历史浏览了10个商户,这些商户id的常规处理方法是作为同一个领域的特征嵌入后直接求和得到一个嵌入向量。但这10个商户只有一两个商户与当前被预测的广告所在的商户相似,其他商户关系不大。增加这两个商户在求和过程中的权重,应该能够更好地提高模型的表现力。而增加求和权重的思路就是典型的注意力机制思路。
由 **Bahdanau et al. (2015) **引入的现代注意力机制,本质上是加权平均(权重是模型根据数据学习出来的),其在机器翻译上应用得非常成功。受注意力机制的启发,Guorui Zhou等在2017年提出了深度兴趣网络(Deep Interest Network,DIN)。DIN主要关注用户在同一领域的历史行为特征,如浏览了多个商家、多个商品等。DIN可以对这些特征分配不同的权重进行求和。其网络结构图如下:
![]()
- 此处采用原论文的结构图,表示起来更清晰。
- DIN考虑对同一领域的历史特征进行加权求和,以加强其感兴趣的特征的影响。
- 用户的每个领域的历史特征权重则由该历史特征及其对应备选广告特征通过一个子网络得到。即用户历史浏览的商户特征与当前浏览商户特征对应,历史浏览的商品特征与当前浏览商品特征对应。
- 权重子网络主要包括特征之间的元素级别的乘法、加法和全连接等操作。
- AFM也引入了注意力机制。但是AFM是将注意力机制与FM同领域特征求和之后进行结合,DIN直接是将注意力机制与同领域特征求和之前进行结合。
16.多任务视角:信息的迁移与补充
对于数据驱动的解决方案而言,数据和模型同样重要,数据(特征)通常决定了效果的上限,各式各样的模型会以不同的方式去逼近这个上限。而所有算法应用的老司机都知道很多场景下,如果有更多的数据进行模型训练,效果一般都能显著得到提高。广告也是一样的场景,在很多电商的平台上会有很多不同场景的广告位,每个场景蕴含了用户的不同兴趣的表达,这些信息的汇总与融合可以带来最后效果的提升。但是将不同场景的数据直接进行合并用来训练(ctr/cvr)模型,结果很多时候并不是很乐观,仔细想想也是合理的,不同场景下的样本分布存在差异,直接对样本累加会影响分布导致效果负向。
![]()
而深度学习发展,使得信息的融合与应用有了更好的进展,用 M u l t i − t a s k Multi-task Multi−task l e a r n i n g ( M T L ) learning(MTL) learning(MTL)的方式可以很漂亮的解决上面提到的问题。我们不直接对样本进行累加和训练,而是像上图所示,把两个场景分为两个task,即分为两个子网络。对单个网络而言,底层的embedding层的表达受限于单场景的数据量,很可能学习不充分。而上图这样的网络结合,使得整个训练过程有了表示学习的共享(Shared Lookup Table),这种共享有助于大样本的子任务帮助小样本的子任务,使得底层的表达学习更加充分。 **DeepFM和DCN也用到了这个思路!只是它们是对同一任务的不同模型进行结合,而多任务学习是对不同任务的不同模型进行结合。**而且,我们可以玩得更加复杂。
Multi-task learning(MTL)整个结构的上层的不同的task的子网络是不一样的,这样每个子网络可以各自去拟合自己task对应的概念分布。并且,取决于问题与场景的相似性和复杂度,可以把底层的表达学习,从简单的共享embedding到共享一些层次的表达。极端的情况是我们可以直接共享所有的表达学习(representation learning)部分,而只接不同的网络head来完成不一样的任务。这样带来的另外一个好处是,不同的task可以共享一部分计算,从而实现计算的加速。
值得一提的另一篇paper是阿里妈妈团队提出的“完整空间多任务模型”(Entire Space Multi-Task Model,ESMM),也是很典型的多任务学习和信息补充思路,这篇paper解决的问题不是ctr(点击率)预估而是cvr(转化率)预估,传统CVR预估模型会有比较明显的样本选择偏差(sample selection bias)和训练数据过于稀疏(data sparsity )的问题,而ESMM模型利用用户行为序列数据,在完整的样本数据空间同时学习点击率和转化率(post-view clickthrough&conversion rate,CTCVR),在一定程度上解决了这个问题。
在电商的场景下,用户的决策过程很可能是这样的,在观察到系统展现的推荐商品列表后,点击自己感兴趣的商品,进而产生购买行为。所以用户行为遵循这样一个决策顺序:impression → click → conversion。CVR模型旨在预估用户在观察到曝光商品进而点击到商品详情页之后购买此商品的概率,即pCVR = p(conversion|click,impression)。
预估点击率pCTR,预估点击下单率pCVR和预估点击与下单率pCTCVR关系如下。
![]()
传统的CVR预估任务通常采用类似于CTR预估的技术进行建模。但是不同于CTR预估任务的是,这个场景面临一些特有的挑战:1) 样本选择偏差;2) 训练数据稀疏;3) 延迟反馈等。

EMMS的特点是:
- 在整个样本空间建模。pCVR 可以在先估计出pCTR 和pCTCVR之后计算得出,如下述公式。从原理上看,相当于分别单独训练两个模型拟合出pCTR 和pCTCVR,进而计算得到pCVR 。
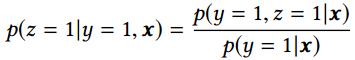
注意到pCTR 和pCTCVR是在整个样本空间上建模得到的,pCVR 只是一个中间变量。因此,ESMM模型是在整个样本空间建模,而不像传统CVR预估模型那样只在点击样本空间建模。 - 特征表示层共享。ESMM模型借鉴迁移学习和multi-task learning的思路,在两个子网络的embedding层共享特征表示词典。embedding层的表达参数占了整个网络参数的绝大部分,参数量大,需要大量的训练样本才能学习充分。显然CTR任务的训练样本量要大大超过CVR任务的训练样本量,ESMM模型中特征表示共享的机制能够使得CVR子任务也能够从只有展现没有点击的样本中学习,从而在一定程度上缓解训练数据稀疏性问题。
17.各种模型的对比和总结
前面介绍了各种基于深度学习的广告点击率预估算法模型,针对不同的问题、基于不同的思路,不同的模型有各自的特点。各个模型具体关系比较如下表1所示:
| Embedding+MLP | FM | Attention | Resnet | |
|---|---|---|---|---|
| Wide&Deep | √ | × | × | × |
| FNN | √ | √ | × | × |
| DeepFM | √ | √ | × | × |
| NFM | √ | √ | × | × |
| DIN | √ | × | √ | × |
| AFM | × | √ | √ | × |
| Deep Cross | √ | × | × | √ |
| DCN | √ | √ | × | √ |
本文从开篇就说明这些模型推演的核心思路是“通过设计网络结构进行组合特征的挖掘”,其在各个模型的实现方式如下:
- FM其实是对嵌入特征进行两两内积实现特征二阶组合;FNN在FM基础上引入了MLP;
- DeepFM通过联合训练、嵌入特征共享来兼顾FM部分与MLP部分不同的特征组合机制;
- NFM、PNN则是通过改造向量积的方式来延迟FM的实现过程,在其中添加非线性成分来提升模型表现力;
- AFM更进一步,直接通过子网络来对嵌入向量的两两逐元素乘积进行加权求和,以实现不同组合的差异化,也是一种延迟FM实现的方式;
- DCN则是将FM进行高阶特征组合的方向上进行推广,并结合MLP的全连接式的高阶特征组合机制;
- Wide&Deep是兼容手工特征组合与MLP的特征组合方式,是许多模型的基础框架;
- Deep Cross是引入残差网络机制的前馈神经网络,给高维的MLP特征组合增加了低维的特征组合形式,启发了DCN;
- DIN则是对用户侧的某历史特征和广告侧的同领域特征进行组合,组合成的权重反过来重新影响用户侧的该领域各历史特征的求和过程;
- 多任务视角则是更加宏观的思路,结合不同任务(而不仅是同任务的不同模型)对特征的组合过程,以提高模型的泛化能力。
当然,广告点击率预估深度学习模型还有很多,比如Jie Zhu提出的基于决策树的神经网络(Deep Embedding Forest)将深度学习与树型模型结合起来。如果数据特征存在图像或者大量文本相关特征,传统的卷积神经网络、循环神经网络均可以结合到广告点击率预估的场景中。各个深度模型都有相应的特点,限于篇幅,我们就不再赘述了。
18.后记
目前深度学习的算法层出不穷,看论文确实有些应接不暇。我们的经验有两点:要有充分的生产实践经验,同时要有扎实的算法理论基础。很多论文的亮点其实是来自于实际做工程的经验。也辛亏笔者一直都在生产一线并带领算法团队进行工程研发(当然也因此荒废了近2年的博客,T△T ),积淀了一些特征工程、模型训练的经验,才勉强跟得上新论文。比如DIN“对用户侧的某领域历史特征基于广告侧的同领域特征进行加权求和”的思想,其实与传统机器学习对强业务相关特征进行针对性特征组合的特征工程思路比较相似。另一方面,对深度学习的经典、前沿方法的熟悉也很重要。从前面我们的串讲也能够看出,CTR预估作为一个业务特点很强的场景,在应用深度学习的道路上,也充分借鉴了注意力机制、残差网络、联合训练、多任务学习等经典的深度学习方法。了解博主的朋友也知道我们一直推崇理论与实践相结合的思路,我们自身对这条经验也非常受用。当然,计算广告是一个很深的领域,自己研究尚浅,串讲难免存在纰漏。欢迎大家指出问题,共同交流学习。
参考文献
-
陈巧红,余仕敏,贾宇波. 广告点击率预估技术综述[J]. 浙江理工大学学报. 2015(11).
-
纪文迪,王晓玲,周傲英. 广告点击率估算技术综述[J]. 华东师范大学学报(自然科学版). 2013(03).
-
Rendle S. Factorization machines. Data Mining (ICDM), 2010 IEEE 10th International Conference on. 2010.
-
Heng-Tze Cheng and Levent Koc. Wide & deep learning for recommender systems. In Proceedings of the 1st Workshop on Deep Learning for Recommender Systems, pages 7–10. ACM, 2016.
-
Weinan Zhang, Tianming Du, and Jun Wang. Deep learning over multi-field categorical data - - A case study on user response prediction. In ECIR, 2016.
-
Huifeng Guo, Ruiming Tang, Yunming Ye, Zhenguo Li, and Xiuqiang He. DeepFM: A Factorization-Machine based Neural Network for CTR Prediction. arXiv preprint arXiv:1703.04247 (2017).
-
Xiangnan He and Tat-Seng Chua. Neural Factorization Machines for Sparse Predictive Analytics SIGIR. 355–364. 2017.
-
Guorui Zhou, Chengru Song, Xiaoqiang Zhu, Xiao Ma, Yanghui Yan, Xingya Dai, Han Zhu, Junqi Jin, Han Li, and Kun Gai. 2017. Deep Interest Network for Click-Through Rate Prediction. arXiv preprint arXiv:1706.06978 (2017).
-
J. Xiao, H. Ye, X. He, H. Zhang, F. Wu, and T.-S. Chua. Attentional factorization machines: Learning the weight of feature interactions via attention networks. In IJCAI, 2017.
-
Ying Shan, T Ryan Hoens, Jian Jiao, Haijing Wang, Dong Yu, and JC Mao. 2016. Deep Crossing: Web-Scale Modeling without Manually Cra ed Combinatorial Features. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 255–262.
-
Wang, R., Fu, B., Fu, G., Wang, M.: Deep & cross network for ad click predictions. In: Proceedings of the ADKDD 17. pp. 12:1–12:7 (2017).
-
Ying Shan, T Ryan Hoens, et al. Deep crossing: Web-scale modeling without manually crafted combinatorial features. KDD ’16. ACM, 2016.
-
Paul Covington, Jay Adams, and Emre Sargin. Deep neural networks for youtube recommendations. In Proceedings of the 10th ACM Conference on Recommender Systems, pages 191–198. ACM, 2016.
-
Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2015. Deep residual learning for image recognition. arXiv preprint arXiv:1512.03385 (2015).