第一章 引言 (数据结构与算法)
第一章 引言
- 第一章 引言
-
- 三个问题
-
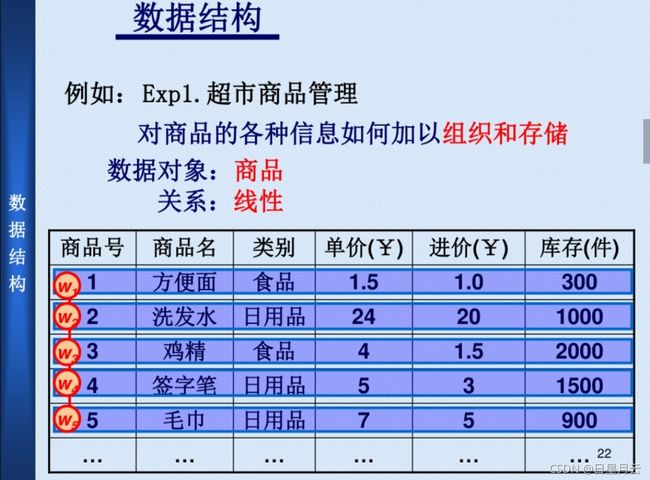
- 超市商品问题
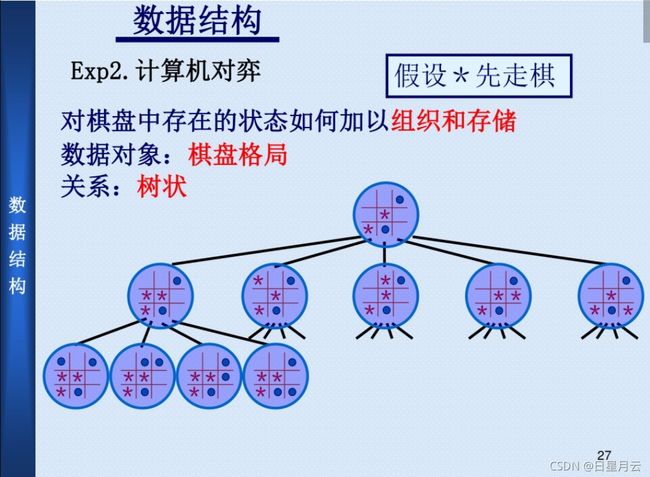
- 人机对弈问题
- 多岔路口交通灯的管理问题
- 1.1 数据结构的概念
- 1.2 数据结构的内容
-
- 1.2.1 数据的逻辑结构
- 1.2.2 数据的存储结构
- 1.3 算法
-
- 1.3.1 算法的概念
- 1.3.2 算法的评价标准
- 1.3.3 算法的描述
- 1.3.4 算法性能分析
-
- 1.时间复杂度
- 2.空间复杂度
- 习题1
-
- 题 6 9
- 解
本类文章只介绍学习中重点
书本的节选内容
第一章 引言
数据结构是一门讨论“描述现实世界实体的数学模型(非数值计算)及其上的操作在计算机中如何表示和实现”的学科。
主要研究数据(特别是非数值型数据) 的组织、存储和运算方法的课程。
计算机科学中的一门综合性的专业基础课。
学会分析数据对象的特征,掌握数据的组织方法和计算机的表示方法,以便为应用所涉及的数据选择适当的逻辑结 构、存储结构及相应算法,初步掌握算法时间及空间分析的 技巧,培养良好的程序设计技能。
学习方法:
学习数据结构,必须经过大量的实践,在实践中体会构 造性思维方法,掌握数据组织与程序设计的技术。
编程没有捷径–“练、练、练”。
三个问题
超市商品问题
人机对弈问题
多岔路口交通灯的管理问题
数据结构
概括:
为在计算机上解决具体问题,应如何对所需的数据/信息及其关系进行组 织,以及如何对它们进行基本操作。
简言之,就是研究数据的组织 方式(结构)及相应的抽象操作。
1.1 数据结构的概念
- 数据对象是性质相同的数据元素的集合
- 数据结构是指相互存在一种或多种特定关系的数据元素的集合。
例如表结构(线性关系)、树形结构(一对多的层次关系)、图结构(多对多的任意关系)
研究问题的一般思路:1.找数据对象 2、找数据结构 3、存储 4、操作
1.2 数据结构的内容
包含三方面内容:数据的逻辑结构、数据的存储结构、数据的运算
1.2.1 数据的逻辑结构
①集合结构:结构中的数据元素之间除了同属于一个集合的关系外,无任何其他关系。
②线性结构:结构中的数据元素之间存在着一对一的线性关系。
③树形结构:结构中的数据元素之间存在着一对多的层次关系。
④图状结构.结构中的数据元素之间存在着多对多的任意关系。
1.2.2 数据的存储结构
顺序存储 链式存储
- 顺序存储的特点是借助元素在存储器中的相对位置来表示数据元素之间的逻辑关系
- 链式存储的特点是借助指针表示数据元素之间的逻辑关系
1.3 算法
1.3.1 算法的概念
- 算法就是解决问题的一系列操作步骤的集合。
- 算法的特性:1、有穷性 2、确定性 3、可行性 4、有输入 5、有输出
1.3.2 算法的评价标准
- 正确性
- 可读性
- 健壮性(鲁棒性)
- 高效率和低存储量需求
1.3.3 算法的描述
一般采用类语言描述算法
1.3.4 算法性能分析
1.时间复杂度
一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数f(n),算法的时间度量记作T(n)=O(f(n))。它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称为算法的“时间复杂度”。
O的数学含义是,若存在两个常量C和n0,当n>n0时,
|T(n)|<=C|f(n)|
则记作
T(n)=O(f(n))
算法语句 对应的语句频度
for(i=0;i<n;i++) n+l
for(j=0;j<n;j++) n(n+1)
{
c[i][j]=0; n*n
for (k=0;k<n;k++) n*n*(n+1)
c[i][j] =c[i][j] +a[i] [k]*b[k][j];(原操作) n*n*n
}
- 最坏时间复杂度
2.空间复杂度
空间复杂度是指算法在计算机内执行时所需存储空间的度量,记作
S(n)=O(f(n))
算法执行期间所需要的存储空间包括三部分。
①算法程序所占的空间。
②输入的初始数据所占的存储空间。
③算法执行过程中所需要的额外空间。
若输入数据所占空间只取决于问题本身,和算法无关,则只需要分析除输入和程序之外的辅 助变量所占的额外空间。
若所需额外空间相对于输人数据量来说是常数,则称此算法为“原地工作”。
若所需存储量依赖于特定的输人,则通常按最坏情况考虑。
习题1
题 6 9
- 6.设n为正整数,请估算以下程序段的时间复杂度。
(1)
i=1;k=0;
while(i<=n-1)
{
k=k+10*i;
i++;
}
(2)
i=1;j=0;
while(i+j<=n)
{
if(i>j) j++
else i++;
}
(3)
x=n;y=0;/*n>1*/
while(x>=(y+1)*(y+1))
y++;
(4)
x=91;y=100;
while(y>0)
{
if(x>100)
{
x=x-10;
y--;
}
else x++;
}
- 9.算法设计:设计求解下列问题的类C语言算法,并分析其最环情况下的时间复杂度。
- (1)在数组A[1…n]中查找值为K的元素,若找到则输出其位置i(1<=i<=n),否则输出0作为标志
- (2)找出数组A[1…n]中元素的最大值和次最大值(本小题以数组元素的比较为标准操作)。
解
(1)
i=1;k=0;
while(i<=n-1)
{
k=k+10*i;
i++;
}
T(n)=O(n)
(2)
i=1;j=0;
while(i+j<=n)
{
if(i>j) j++
else i++;
}
T(n)=O(n)
(3)
x=n;y=0;/*n>1*/
while(x>=(y+1)*(y+1))
y++;
T(n)=O(n^(1/2))
(4)
x=91;y=100;
while(y>0)
{
if(x>100)
{
x=x-10;
y--;
}
else x++;
}
T(n)=O(1)
9.1
typedef int Type;
int find(Tyde A[],int len Type K){
//len等于题中的n+1
A[0]=K;
for(i=n;i>-1;i--){
if(A[i]==K){
return i;
}
}
T(n)=O(n)
9.2
typedef int Type;
void find(Type A[],int len,Type *max1,Type *max2){
//*max1表示最大值,*max2表示次大值//len等于题中的n+1
if(A[1]>=A[2]){
*max1=A[1];
*max2=A[2];
}else{
*max1=A[2];
*max2=A[1];
}
for(i=3;i<n+1;i++){
if(A[i]>*max1){
*max2=*max1;
*max1=A[i];
}else if(A[i]>*max2){
*max2=A[i];
}
}
}
T(n)=O(n)