基于python的时间序列分析ARIMA（p,d,q）模型及模型预测

原理请查阅相关图书

本文建立于Anaconda  可能部分代码不适用于IDLE编译器需要轻微改动

首先应导入所需要的第三方库。

import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
from statsmodels.stats.diagnostic import acorr_ljungbox
from statsmodels.tsa.stattools import adfuller as ADF
from statsmodels.tsa.arima.model import ARIMA
from datetime import datetime
from itertools import product
import numpy as np
import warnings

首先观察时间序列是否平稳。（若平稳d=0，差分一次d=1，两次d=2，若差分两次依旧不平稳则应该取其它方法去平稳化，例如取对数等）

绘制时序图并进行单位根检验

#差分
D_data = plist.diff( ).dropna()#一阶差分
D_data2 = D_data.diff().dropna()#二阶差分
#绘制时序图
plt.figure()
plt.subplot(2,1,1)
D_data.plot()
plt.subplot(2,1,2)
D_data2.plot()
#plot_acf(D_data)
plt.show()
print(u'D_data序列的ADF检验结果为：',ADF(D_data))  #ADF检验为单位根检验
print(u'D_data2序列的ADF检验结果为：',ADF(D_data2))
print(u'2阶差分序列的白噪声检验结果为：', acorr_ljungbox(D_data2, lags=1))  

结果

 可见原始序列既有长期增长趋势和周期趋势，单位根检验结果为4.527751671288059，p值为1大于0.1可见是不平稳的。（p小于0.1即可，p值越小越好）

一阶差分序列ADF检验结果为-2.582876243723786，p值为0.09左右。可以接受。

二阶差分序列ADF检验结果为-9.962807970208384，p值为2.3491418740807038乘10的-17次方。效果很好，我们采用二阶差分结果。

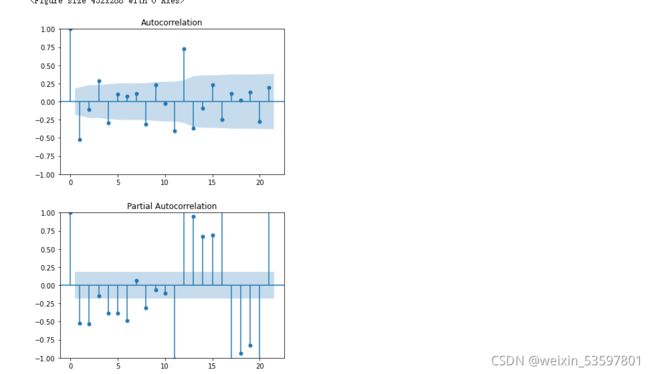
接下来绘制自相关与偏自相关图

plt.figure()
plot_acf(D_data2)
plot_pacf(D_data2)
plt.show()

结果

 很难看出自相关与偏自相关函数是拖尾还是结尾（判断依据如下图）差分后的序列要使用ARIMA算法。

 接下来进行定阶我们采用BIC准则（越小越好）来定阶。本文提供三种定阶方法（三种方法均可）

#方法一 通过bic矩阵定阶
pmax = 10 #一般不会大于10
qmax = 10 #一般不会大于10
bic_matrix = []
for p in range(pmax):
    temp= []
    for q in range(qmax):
        try:
            temp.append(ARIMA(plist,order=(p, 2, q)).fit().bic)
        except:
            temp.append(None)
        bic_matrix.append(temp)
bic_matrix = pd.DataFrame(bic_matrix)  
p,q = bic_matrix.stack().idxmin()   
print(u'BIC 最小的p值 和 q 值：%s,%s' %(p,q)) 


#方法二 通过遍历定阶。
tmp = []
for p in range(10):
    for q in range(10):
        try:
            tmp.append([ARIMA(plist,order=(p,1,q)).fit().bic,p,q])
        except:
            tmp.append([None,p,q])
 
tmp = pd.DataFrame(tmp,columns = ['bic','p','q'])
tmp[tmp['bic'] ==tmp['bic'].min()]



方法三 #从结果出发定阶
for i in range(13):
    print("AR({})".format(i))
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
    plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
    model = ARIMA(plist,order=(i,2,5)).fit() # 建立ARIMA模型
    predictions_ARIMA_diff = pd.Series(model.fittedvalues, copy=True)
    #print(predictions_ARIMA_diff.head())
    plt.figure(figsize=(10, 6))
    plt.plot(predictions_ARIMA_diff,label="预测数据")
    plt.plot(plist,label="原始数据")
    plt.xlabel('日期序列',fontsize=12,verticalalignment='top')
    plt.ylabel('客运量',fontsize=14,horizontalalignment='center')
    plt.legend()
    plt.show()
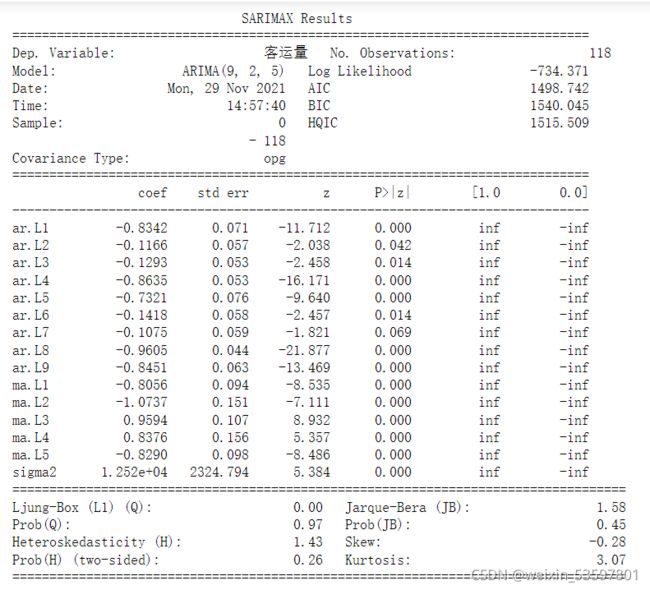
    print(model.summary(2))

作者的定阶结果为ARIMA（9,2,5）模型报告为。

model = ARIMA(plist,order=(9,2,5)).fit() 
print(model.summary(2))

 模型拟合

plt.figure(figsize=(10, 6))
plt.plot(predictions_ARIMA_diff,label="预测数据")
plt.plot(plist,label="原始数据")
plt.xlabel('日期序列',fontsize=12,verticalalignment='top')
plt.ylabel('客运量',fontsize=14,horizontalalignment='center')
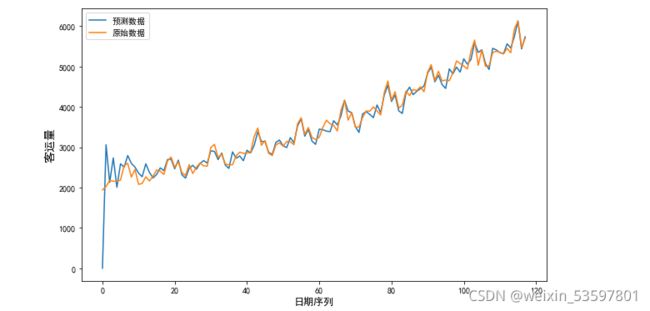
plt.legend()
plt.show()

 模型拟合效果十分不错（可以进行残差检验等在此处略）

进行预测

print('预测2021 1季度，其预测结果、标准误差、置信区间如下：\n', model.forecast(1))#预测1期