leetcode-day11:Intersection of Two Linked Lists(链表相交)
160. Intersection of Two Linked Lists
链表:链表相交
Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.
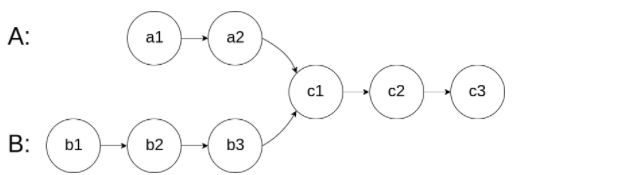
For example, the following two linked lists begin to intersect at node c1:
The test cases are generated such that there are no cycles anywhere in the entire linked
structure.Note that the linked lists must retain their original structure after the
function returns.
Custom Judge:
The inputs to the judge are given as follows (your program is not given these inputs):
- intersectVal - The value of the node where the intersection occurs. This is 0 if there is no intersected node.
- listA - The first linked list.
- listB - The second linked list.
- skipA - The number of nodes to skip ahead in listA (starting from the head) to get to the intersected node.
- skipB - The number of nodes to skip ahead in listB (starting from the head) to get to the intersected node.
The judge will then create the linked structure based on these inputs and pass the two heads, headA and headB to your program. If you correctly return the intersected node, then your solution will be accepted.
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output: Intersected at '8'
Explanation: The intersected node's value is 8 (note that this must not be 0 if the
two lists intersect).
From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,6,1,8,4,5].
There are 2 nodes before the intersected node in A; There are 3 nodes
before the intersected node in B.
Example 2:
Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Intersected at '2'
Explanation: The intersected node's value is 2 (note that this must not be 0 if the two
lists intersect).
From the head of A, it reads as [1,9,1,2,4]. From the head of B, it reads as [3,2,4].
There are 3 nodes before the intersected node in A; There are 1 node before the intersected
node in B.
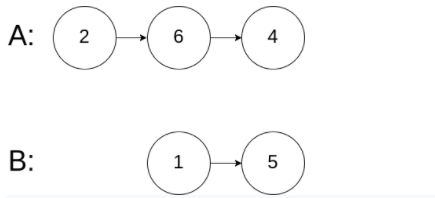
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: No intersection
Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5].
Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can
be arbitrary values.
Explanation: The two lists do not intersect, so return null.
Constraints:
The number of nodes of listA is in the m.
The number of nodes of listB is in the n.
0 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
intersectVal is 0 if listA and listB do not intersect.
intersectVal == listA[skipA] == listB[skipB] if listA and listB intersect.
Follow up: Could you write a solution that runs in O(n) time and use only O(1) memory?
JAVA实现代码:
/**
编码逻辑:
1.两单链表右对齐
2.同时向后移动,判断为同一个引用时停止
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
//求长度
int lenA=0;
ListNode curA = headA;
int lenB=0;
ListNode curB=headB;
while(curA!=null){
lenA++;
curA=curA.next;
}
while(curB!=null){
lenB++;
curB=curB.next;
}
curA = headA;
curB = headB;
int startIndex=0;
//求长度差
if(lenA>lenB){
ListNode tempNode = curA;
curA=curB;
curB=tempNode;
int temp=lenA;
lenA=lenB;
lenB=temp;
}
//对齐数据
startIndex = lenB-lenA;
int i=0;
while(i++<startIndex){
curB=curB.next;
}
ListNode intersectNode=null;
while(curB!=null){
if(curB.equals(curA)){
intersectNode=curB;
break;
}
curB=curB.next;
curA=curA.next;
}
return intersectNode;
}
}