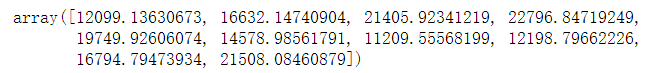arima模型 p q d 确定_时间序列ARMA和ARIMA
↑ 点击上方 “凹凸数据” 关注 + 星标 ~
每天更新，大概率是晚9点
本文作者：吴达科，授权投稿
首发于CSDN：https://blog.csdn.net/qq_33333002/article/details/106171234
1.简介
1.1 时间序列包括：
AR(自回归模型)，AR ( p) ，p阶的自回归模型 MA(移动平均模型)，MA(q)，q阶的移动平均模型 ARIMA(差分自回归移动平均模型)
1.2 运用对象
这里四种模型都是变量y，针对时间变化而发生的改变，这四种模型的运用对象都是平稳的时间序列。也就是随着时间的变化，在一定范围内动态波动。不平稳序列如下图所示：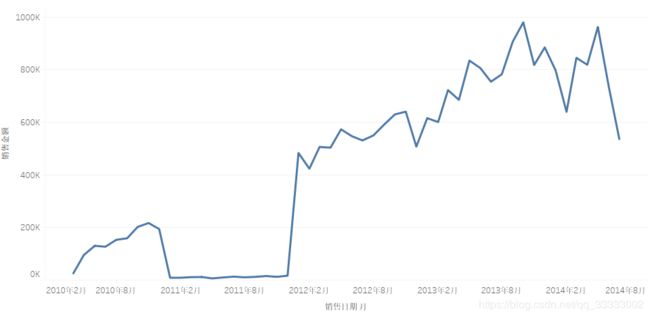
平稳序列如下图所示：
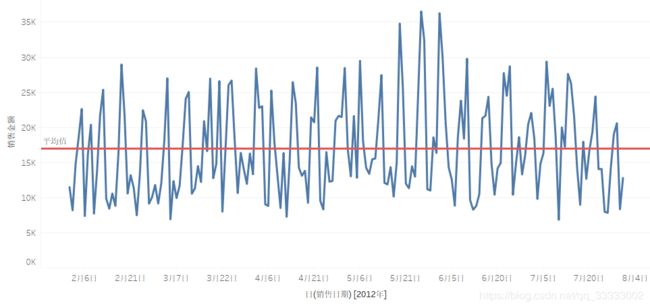AR,MA,ARMA都是运用于原始数据是平稳的时间序列。ARIMA运用于原始数据差分后是平稳的时间序列。
该文章是基于时间序列的ARMA、ARIMA模型，来进行实践。这里只对销售金额进行分析。
2. 数据的导入、清洗
2.1 导入数据，进行探索性分析
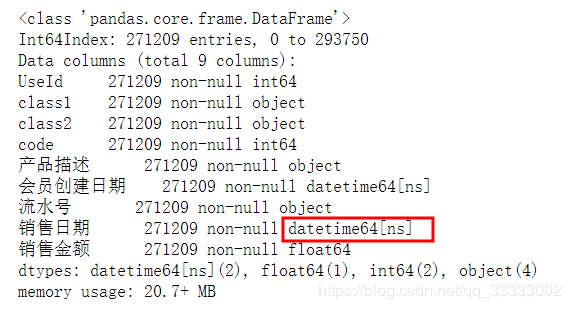
import numpy 输出：
查看表的结构：
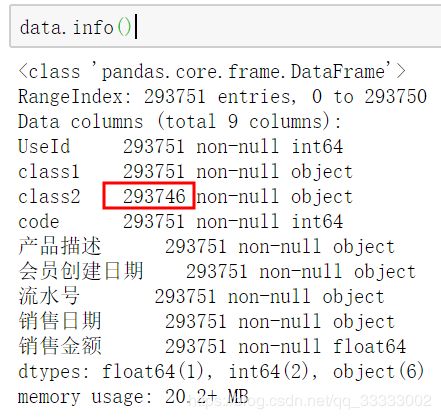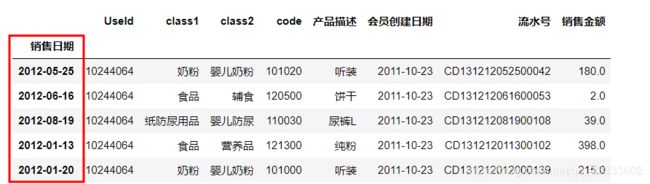
这里的class2有5个缺失值，由于这里不对此进行分析，就不进行该数据的清洗。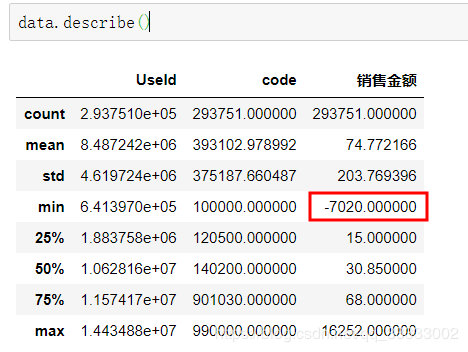
销售金额这里有负数，负数的原因可能是因为退货，销售金额是0的情况可能是因为积分兑换这样的活动。
2.2 数据的清洗
这里将销售额小于等于0的情况直接过滤掉。
'销售金额'] > 将销售日期转换成datetime类型，并设置为索引
'销售日期'] = pd.to_datetime(data[输出：
'销售日期', inplace=输出：
至此数据清洗完毕。
3. 进行ARMA分析
3.1 提取部分数据进行分析
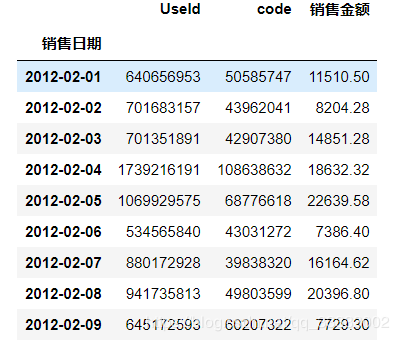
这里直接筛选一段销售金额较平稳的日期(2012-02-01到2012-07-31的182条每天的销售金额)来做分析。提取数据
# 筛选2012-02-01到2012-07-31的日期输出：
3.2 进行平稳性检验
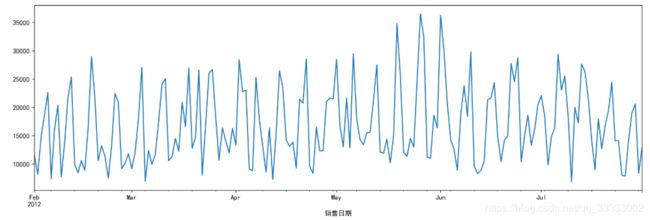
3.2.1 时序图
时序图可以看出销售金额是在一定范围内动态波动。从图中可以看出2012-02-01到2012-07-31的182条每天的销售金额是在一定范围内动态波动的。
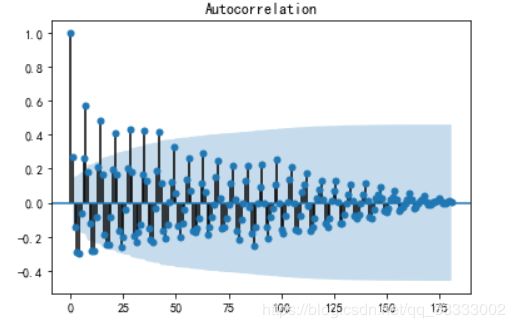
16, 输出：
3.2.2 自相关图
from statsmodels.graphics.tsaplots 输出：
3.2.3 偏自相关图
from statsmodels.graphics.tsaplots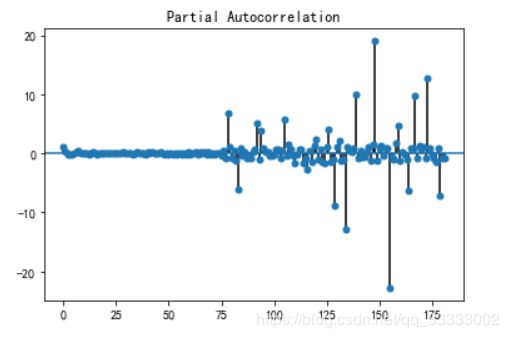 
3.2.4 单位根检验
单位根检验主要是检验p值是否大于0.05，大于0.05的时间序列是非平稳的，需要进行差分。p值小于0.05的是平稳的时间序列。
from statsmodels.tsa.stattools 输出：
这里的第二个值就是p值。这里的p值小于0.05。判断选取的数据是平稳的时间序列。
3.2.5 白噪声检验
白噪声检验主要是检验p值是否大于0.05，大于0.05的时间序列是平稳的白噪声时间序列，p值小于0.05的是平稳的非白噪声的时间序列，是平稳的非白噪声的时间序列才可以进行下一步的ARMA分析。
from statsmodels.stats.diagnostic 输出：
这里明显小于0.05.判断选取的数据是平稳的非白噪声的时间序列。
3.3 进行ARMA分析
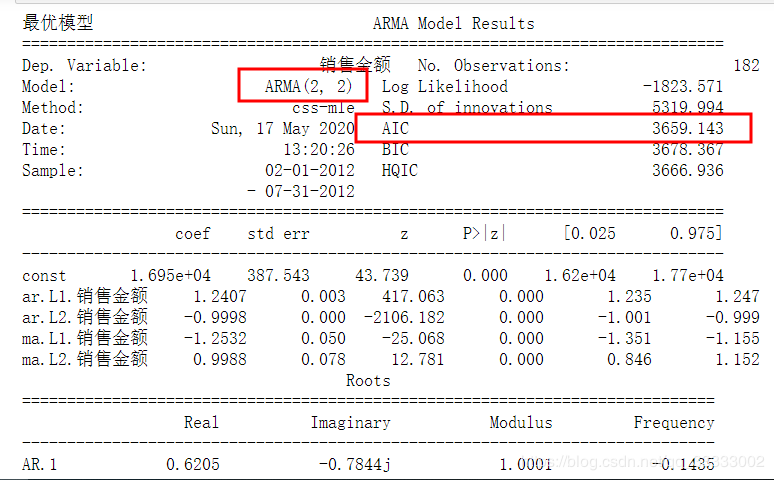
3.3.1 ARMA模型的训练，p阶，q阶最佳参数的确定
最优的模型的AIC最小。
from statsmodels.tsa.arima_model 输出：
3.3.2 最优模型进行预测
预测后面10天的销售金额
10)[输出：
4. 进行ARIMA分析
4.1 提取部分数据进行分析
这里选取2012-09-01到2012-12-21的每天的销售金额汇总
'2012-09-01') & (data.index <= 4.2 进行平稳性检验
4.2.1 时序图
16,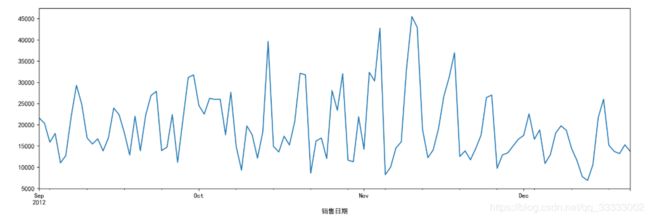 
在这里插入图片描述
4.2.2 自相关图
25,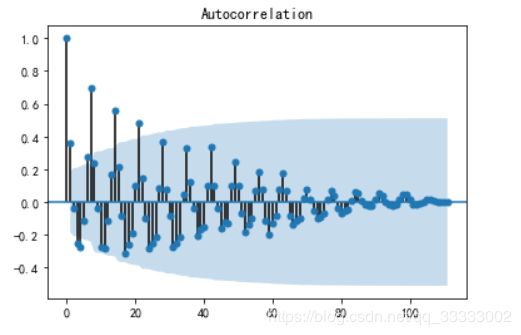 
4.2.3 偏自相关图
25,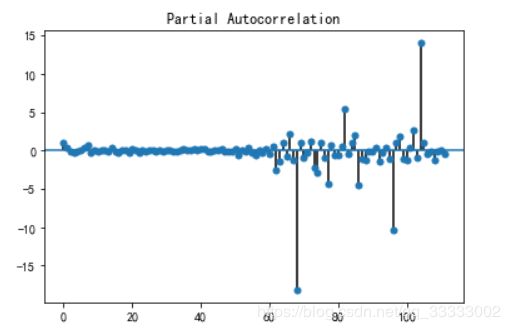 
4.2.4 单位根检验
from statsmodels.tsa.stattools 
单位根检验的p值大于0.05，需要差分再重新进行单位根检验
'销售金额'].diff().dropna()
一阶差分后p值小于0.05，一阶差分后属于平稳序列。
4.2.5 白噪声检验
from statsmodels.stats.diagnostic 
白噪声的p值小于0.05。经一阶差分后，该序列属于平稳非白噪声序列，这里可以使用ARIMA模型进行分析预测。
4.3 进行ARIMA分析
4.3.1 ARIMA模型的训练，p阶，q阶最佳参数的确定
from statsmodels.tsa.arima_model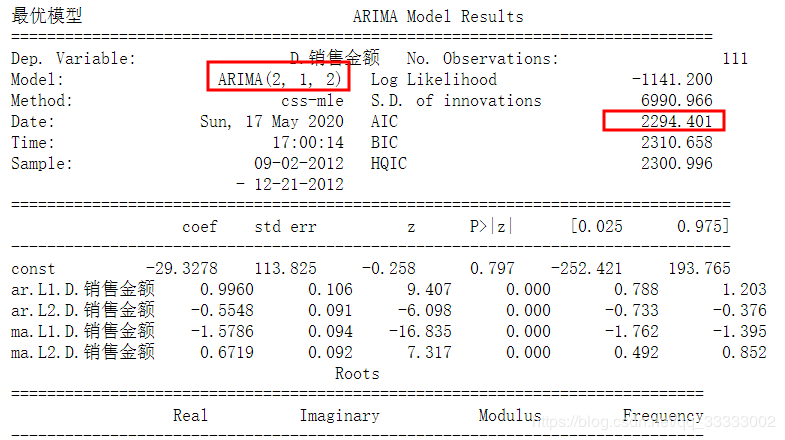 
4.3.2 最优模型进行预测
预测后面10天的销售金额
10)[
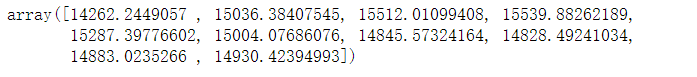4.3.3 模型评价
from sklearn.metrics 
这里的平均绝对误差为4.5，这里要根据实际的业务确定误差阈值。再来进行模型的评价。小于阈值的，模型就是稍微好的，大于阈值的，说明模型的准确率还有待提高，模型还需重新训练等。
后台回复「进群」，加入读者交流群~
