1. 递归函数
# ### 递归函数
"""
递归函数 : 自己调用自己的函数 , 叫做递归函数
递 : 去
归 : 回
一去一回叫做递归
"""
def digui(n):
print(n,"<==1==>")
if n > 0:
digui(n-1)
print(n,"<==2==>")
digui(5)
"""
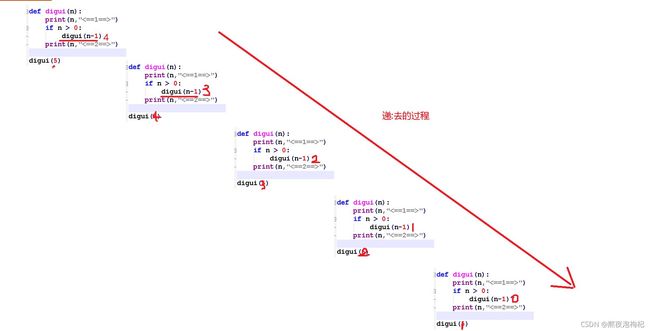
# 去的过程
n = 5 print(5,"<==1==>") if 5 > 0: digui(5-1) => digui(4) 代码阻塞在第12行
n = 4 print(4,"<==1==>") if 4 > 0: digui(4-1) => digui(3) 代码阻塞在第12行
n = 3 print(3,"<==1==>") if 3 > 0: digui(3-1) => digui(2) 代码阻塞在第12行
n = 2 print(2,"<==1==>") if 2 > 0: digui(2-1) => digui(1) 代码阻塞在第12行
n = 1 print(1,"<==1==>") if 1 > 0: digui(1-1) => digui(0) 代码阻塞在第12行
n = 0 print(0,"<==1==>") if 0 > 0: 不成立 print(0,"<==2==>") 到此最后一层函数空间彻底执行完毕
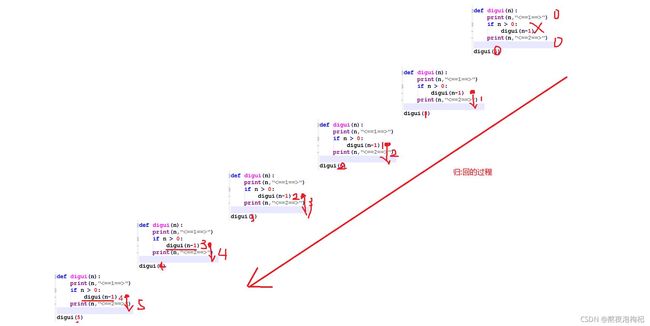
# 回的过程
回到上一层函数空间 n = 1 代码在第12行的位置,继续往下执行 print(1,"<==2==>")
回到上一层函数空间 n = 2 代码在第12行的位置,继续往下执行 print(2,"<==2==>")
回到上一层函数空间 n = 3 代码在第12行的位置,继续往下执行 print(3,"<==2==>")
回到上一层函数空间 n = 4 代码在第12行的位置,继续往下执行 print(4,"<==2==>")
回到上一层函数空间 n = 5 代码在第12行的位置,继续往下执行 print(5,"<==2==>")
到此递归函数执行结束..
打印 543210012345
"""
"""
每次调用函数时,都要单独在内存当中开辟空间,叫做栈帧空间,以运行函数中的代码
递归总结:
(1)递归实际上是不停的开辟栈帧空间和释放栈帧空间的过程,开辟就是去的过程,释放就是回的过程
(2)递归什么时候触发归的过程:
1.当最后一层栈帧空间执行结束的时候,触发归的过程.
2.当遇到return返回值的时候终止当前函数,触发归的过程.
(3)递归不能无限的去开辟空间,可能造成内存溢出,蓝屏死机的情况,所以一定要给予跳出的条件(如果递归的层数太大,不推荐使用)
(4)开辟的一个个栈帧空间,数据是彼此独立不共享的.
"""
# 递归不能不限开辟空间
"""官方说法最大默认是1000层."""
def deepfunc():
deepfunc()
deepfunc()
2. 递归练习
# ### 1.使用递归实现任意数n的阶乘
# 普通实现
# 5! =5 *4*3*2*1
n = 5
total = 1
for i in range(n,0,-1):
total *= i
print(total) # 120
# 递归实现
def jiecheng(n):
if n <= 1:
return 1
return jiecheng(n-1) * n
print(jiecheng(2))
# jiecheng(1) => 1
# jiecheng(2) => jiecheng(1) * 2 => 1 * 2
# jiecheng(3) => jiecheng(2) * 3 => 1 * 2 * 3
# jiecheng(4) => jiecheng(3) * 4 => 1 * 2 * 3 * 4
# jiecheng(5) => jiecheng(4) * 5 => 1 * 2 * 3 * 4 * 5
print(jiecheng(5))
"""
代码解析:
去的过程:
n = 5 return jiecheng(n-1) * n => jiecheng(4) * 5
n = 4 return jiecheng(n-1) * n => jiecheng(3) * 4
n = 3 return jiecheng(n-1) * n => jiecheng(2) * 3
n = 2 return jiecheng(n-1) * n => jiecheng(1) * 2
n = 1 return 1
回的过程:
n = 2 return jiecheng(1) * 2 => 1 * 2
n = 3 return jiecheng(2) * 3 => 1 * 2 * 3
n = 4 return jiecheng(3) * 4 => 1 * 2 * 3 * 4
n = 5 return jiecheng(4) * 5 => 1 * 2 * 3 * 4 * 5
到此程序结束:
返回 1 * 2 * 3 * 4 * 5
"""
print("<====================>")
# ### 2. 使用尾递归来实现任意数的阶乘
""" return 在哪调用,在哪返回 """
"""自己调用自己,且返回时非运算表达式,只是函数本身"""
"""
特点:
尾递归只开辟一个空间,不会无限的开辟,在一个空间里面去计算最后的结果进行返回,比较节省空间,有的解释器支持尾递归的调用特点
但是cpython解释器目前不支持
写法:
所有运算的值都在函数的参数中计算完毕,最后返回运算的参数;
"""
def jiecheng(n,endval):
if n <= 1:
return endval
return jiecheng(n-1 , n * endval)
res = jiecheng(5,1) # 5*4*3*2*1
print(res)
"""
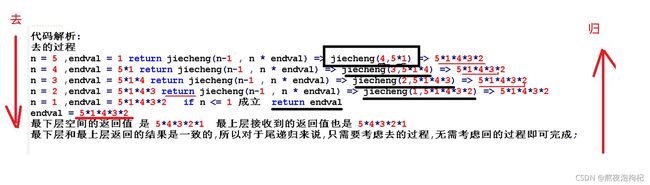
代码解析:
去的过程
n = 5 ,endval = 1 return jiecheng(n-1 , n * endval) => jiecheng(4,5*1) => 5*1*4*3*2
n = 4 ,endval = 5*1 return jiecheng(n-1 , n * endval) => jiecheng(3,5*1*4) => 5*1*4*3*2
n = 3 ,endval = 5*1*4 return jiecheng(n-1 , n * endval) => jiecheng(2,5*1*4*3) => 5*1*4*3*2
n = 2 ,endval = 5*1*4*3 return jiecheng(n-1 , n * endval) => jiecheng(1,5*1*4*3*2) => 5*1*4*3*2
n = 1 ,endval = 5*1*4*3*2 if n <= 1 成立 return endval
endval = 5*1*4*3*2
最下层空间的返回值 是 5*4*3*2*1 最上层接收到的返回值也是 5*4*3*2*1
最下层和最上层返回的结果是一致的,所以对于尾递归来说,只需要考虑去的过程,无需考虑回的过程即可完成;
"""
# 优化代码1
def jiecheng(n,endval=1):
if n <= 1:
return endval
return jiecheng(n-1 , n * endval)
res = jiecheng(5,100) # 5*4*3*2*1
print(res,"<00000>")
# 优化代码2 [把尾递归需要的参数值隐藏起来,避免篡改.]
def outer(n):
def jiecheng(n,endval=1):
if n <= 1:
return endval
return jiecheng(n-1 , n * endval)
return jiecheng(n,1)# 120
print(outer(5))
# 优化代码3(扩展)
# 闭包实现
def outer(n):
endval = 1
def jiecheng(n):
nonlocal endval
if n <= 1:
return endval
endval *= n
return jiecheng(n-1)
return jiecheng
func = outer(5)
print(func(5),"<===111==>")
print("<================>")
# ### 3.使用递归来完成斐波那契数列
""" 1 1 2 3 5 8 13 21 34 ... """
def feib(n):
if n == 1 or n == 2:
return 1
# 上一个结果 + 上上个结果
return feib(n-1) + feib(n-2)
print(feib(5))
"""
# 代码解析:
n = 5 feib(5) => 3 + 2 => return 5
feib(4) + feib(3)
feib(3)+feib(2) feib(2)+feib(1) => 1 + 1 => 2
feib(2)+feib(1)+feib(2) => 1 + 1 + 1 => 3
"""
3. 小练习
# (选做)
# 1.可滑动的序列 自定义一个函数 根据参数n的值 , 变成对应个元素的容器 (zip)
"""
listvar = [1,2,3,4,5,6,7,8,9]
n = 2
listvar = [[1,2],[3,4],[5,6],[7,8]]
n = 3
listvar = [[1,2,3],[4,5,6],[7,8,9]]
n = 4
listvar = [[1,2,3,4],[5,6,7,8]]
"""
"""
lst1 = [1,3,5,7,9]
lst2 = [2,4,6,8]
zip(lst1,lst2)
"""
listvar = [1,2,3,4,5,6,7,8,9]
n = 2
lst1 = [1,3,5,7,9]
lst2 = [2,4,6,8]
# lst1 = listvar[0::2] <=> [1,3,5,7,9]
# lst2 = listvar[1::2] <=> [2,4,6,8]
print(lst2,"1111")
print(list( zip(lst1,lst2) ))
n = 3
lst1 = [1,4,7]
lst2 = [2,5,8]
lst3 = [3,6,9]
# lst1 = listvar[0::3] <=> [1,4,7]
# lst2 = listvar[1::3] <=> [2,5,8]
# lst3 = listvar[2::3] <=> [3,6,9]
print(lst1,"2222")
print(list( zip(lst1,lst2,lst3) ))
n = 4
lst1 = [1,5]
lst2 = [2,6]
lst3 = [3,7]
lst4 = [4,8]
# lst1 = listvar[0::4] <=> [1,5,9]
# lst2 = listvar[1::4] <=> [2,6]
# lst3 = listvar[2::4] <=> [3,7]
# lst4 = listvar[3::4] <=> [4,8]
print(lst1,"3333")
print(list( zip(lst1,lst2,lst3,lst4) ))
print("<=============>")
n = 3
lst = [ listvar[i::n] for i in range(n) ]
print(lst) # [[1, 4, 7], [2, 5, 8], [3, 6, 9]]
# zip(*lst) => zip([1,4,7],[2,5,8],[3,6,9])
it = zip(*lst)
print(list(it))
func = lambda n : zip( *[ listvar[i::n] for i in range(n) ] )
it = func(2)
# 把里面的元组强转成列表
print(list(map(list,it)))
# 2.青蛙跳台阶 (递归实现)
'''
一只青蛙要跳上n层高的台阶
一次能跳一级,也可以跳两级
请问这只青蛙有多少种跳上这个n层高台阶的方法?
n = 1 1 => 1
n = 2 2 => 1 1 | 2
n = 3 3 => 1 1 1 | 1 2 | 2 1
n = 4 5 => 1 1 1 1 | 1 2 1 | 2 1 1 | 1 1 2 | 2 2
n = 5 8 => 1 1 1 1 1 | 1 1 1 2 |2 1 1 1 | 1 2 1 1 | 1 1 2 1 | 2 2 1 | 1 2 2 | 2 1 2
'''
def func(n):
if n == 1 or n == 2:
return n
return func(n-1) + func(n-2)
print(func(5))
# 3.递归反转字符串 "将14235 反转成53241" (递归实现)
# 把后面的字符往前挪动 方法一
strvar = "14235"
# lst.append(5)
# lst.append(3)
# lst.append(2)
# lst.append(4)
# lst.append(1)
# lth = 字符串的总长度 lst 要插入的列表
def func(lth,lst=[]):
if lth == 0:
return lst
res = strvar[lth-1]
lst.append(res)
return func(lth-1)
lth = len(strvar)
lst = func(lth)
print(lst) # ['5', '3', '2', '4', '1']
print("".join(lst))
# 简写
def func(lth,lst=[]):
if lth == 0:
return "".join(lst)
res = strvar[lth-1]
lst.append(res)
return func(lth-1)
print(func(lth))
# 把前面的字符往后挪动 方法二
strvar = "14235"
def func(strvar):
if len(strvar) == 1:
return strvar
return func(strvar[1:])+strvar[0]
res = func(strvar)
print(res)
"""
递:
return func(4235) + 1
return func(235) + 4
return func(35) + 2
return func(5) + 3
return 5
归:
return func(5) + 3 => 5 + 3
return func(35) + 2 => 5 + 3 + 2
return func(235) + 4 => 5 + 3 + 2 + 4
return func(4235) + 1 => 5 + 3 + 2 + 4 + 1
return 5 + 3 + 2 + 4 + 1
"""
# 4.斐波那契数列用尾递归实现
a,b = 0,1
i = 0
n = 5
while i < n:
print(b)
a,b = b,a+b
i +=1
a,b = 0,1
n = 5
while n > 0:
print(b)
a,b = b,a+b
n -= 1
print("<==============>")
def func(n,a=0,b=1):
if n == 1:
return b
return func(n-1,b,a+b)
print(func(6))
总结
本篇文章就到这里了,希望能够给你带来帮助,也希望您能够多多关注脚本之家的更多内容!