graph embedding第一篇——deepwalk and line

参考

graph embedding
深度学习中不得不学的Graph Embedding方法
Embedding从入门到专家必读的十篇论文
DNN论文分享 - Item2vec
从KDD 2018最佳论文看Airbnb实时搜索排序中的Embedding技巧
Negative-Sampling Word-Embedding Method
推荐系统遇上深度学习(四十四)-Airbnb实时搜索排序中的Embedding技巧
理论优美的深度信念网络，Hinton老爷子北大最新演讲

前言

本系列主要介绍graph embedding的一些常用技术以及在推荐领域一些较为成功的graph embedding的应用，如airbnb embedding，阿里提出的EGES。

问题定义：
定义图$G=(V,E)$，其中$V$代表图中所有的顶点，$E$代表所有的边。目标是用低维空间（$d$）的向量表达$V$，其中$d<<|V|$。映射到低维空间后，我们希望仍然保留原graph的一些特性：

• 来自同一个社区的顶点映射的低维embedding尽可能的相似（邻居节点的低维embedding要相似，这可以理解为网络的局部结构）。
• 将来自同一类特殊连接模式的顶点映射低维embedding尽可能的相似（刻画的是网络的全局结构，一般用高阶邻近度刻画）

而且graph emebdding存在的问题：

• 稀疏性：大多数的现实网络非常稀疏，仅仅利用观察到的有限连接难以刻画效果比较好的表征。

DeepWalk

DeepWalk: Online Learning of Social Representations
deepwalk code
【Graph Embedding】DeepWalk：算法原理，实现和应用
deepwalk首次将深度学习技术引入到network分析中，从而学习到图顶点的社交表达social representation。其思想是，对于网络中的任一顶点$u$，采用随机游走技术得到长度为$t$（hyperparameter）的序列，这个序列可以被看成文本序列，利用word2vec技术学习到顶点的表达。

more information about random walk: https://github.com/phanein/deepwalk/blob/master/deepwalk/graph.py

def random_walk(self, path_length, alpha=0, rand=random.Random(), start=None):
   """ Returns a truncated random walk.
       path_length: Length of the random walk.
       alpha: probability of restarts.
       start: the start node of the random walk.
   """
   G = self
   if start:
     path = [start]
   else:
     # Sampling is uniform w.r.t V, and not w.r.t E
     path = [rand.choice(list(G.keys()))]

   while len(path) < path_length:
     cur = path[-1]
     if len(G[cur]) > 0:
       if rand.random() >= alpha:
         path.append(rand.choice(G[cur]))
       else:
         path.append(path[0])
     else:
       break
   return [str(node) for node in path]

思想非常简单，我们来看看其具体算法。

算法

deepwalk:

skipgram:

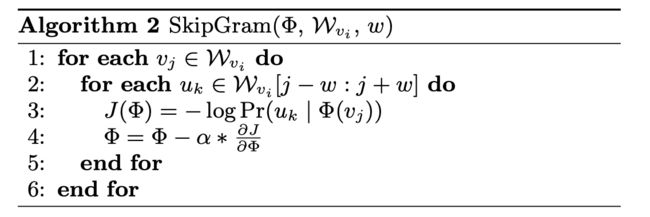
更多的训练细节，可以参考skip-gram的方法，比如：使用Hierarchical Softmax降低计算代价等。这部分内容，都将在word embedding中详述。

hyperparameter 探索

具体分析详见论文6.2.1节。

• 对不同的数据集而言，不同$\gamma$的差异非常一致。
• $\gamma =30$时几乎取得最好效果，继续提升$\gamma$影响不大。
• 对于不同的数据集，不同的$d$与$T_R$的效果比较一致，都是：增加$\gamma$时开始可能有显著的提升，但是当$\gamma >10$时效果开始显著的下降。说明，仅需要少量的随机游走，我们就可以学到有意义的顶点的表示。

缺陷

• 仅适合处理无权图，不适合处理带权重的图。
• 并没有明确表示保留的是顶点的一阶邻近度还是二阶邻近度。

Line

LINE: Large-scale Information Network Embedding
【Graph Embedding】LINE：算法原理，实现和应用
LINE code

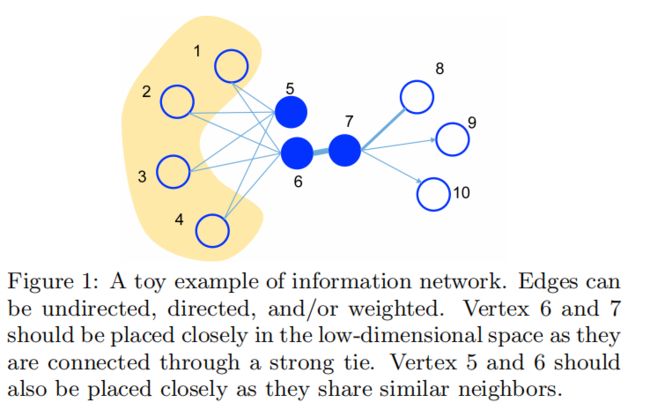
从上图可以看出：

• 顶点6与顶点7直接相连，应该在低维空间中相似度较高（一阶邻近度）
• 但顶点5,6应该也要相似度较高，因为他们共享相似的邻居（二阶邻近度）

Line模型分别为一阶邻近度和二阶邻近度进行建模，建模后的结果分别称之为LINE(1st)与LINE(2nd)。一般来说，对于有监督模型，我们可以将LINE(1st) concat LINE(2nd)；但是对于无监督模型我们只能单独使用其中的一个，因为无监督任务没办法确认他们之间的融合权重。

那么，LINE(1st)和LINE(2nd)都是如何做的呢？

LINE（1st）

为了建模一阶邻近度，对于每一个无向边$(i,j)$，定义顶点$v_i,v_j$之间的联合概率分布为：


想法就是让联合分布与经验分布的KL散度越小越好，优化$O_1$，我们终将获得每个顶点的一阶表达。

LINE(2nd)

对于一阶邻近度我们的目标是与经验分布 越相近越好，那么对于二阶邻近度（考察本节figure 1的顶点5和6）我们的目标为 顶点的邻居节点 越相近越好，为了刻画邻居节点，则需要关注每个顶点对其邻居节点的经验分布：

同样的，定义顶点$v_i$生成器邻居节点$v_j$的条件概率为：

与LINE(1st)相同，目标是二者的KL散度，有：

模型优化

$O_2$的优化：
eq(6)的计算相当低效，这是因为在eq(4)中我们遍历了所有的顶点。这里可以参考skip-gram的negative sampling的方法(越热门的顶点，被采样的概率越高)，将eq(4)修改为：

$O_1$的优化：
目标函数$O_1$含有一个平凡解，即：

但这样的解是没有意义的，因此，为了避免这样的结果，论文同样采用负采样策略：

因为一阶邻近度是无向图，因此要对顶点$i，j$均进行负采样。

边采样

我们采用一步随机梯度下降（ASGD）来优化算法：

由eq(8)可知，每次都要去乘以边的权重，而当边权分布的特别分散时，学习率将难以抉择：

• 我们希望，对于权重较大的边权配以比较小的学习率；但是如果边权较小，将学习缓慢
• 对权重较小配以比较大的学习率，但是如果边权较大，会梯度爆炸。

经上分析，我们自然希望边权是相等的。因此论文提出一个朴素的想法构建二元边，这个策略被称为边采样策略：

1. 令边权$W=\{w_1,w_2,\cdots ,w_{|E|}\}$，计算$w_{s}um$为$W$中所有边权之和。
2. 随机采样一个随机数 S，观察S落入的区间：
   
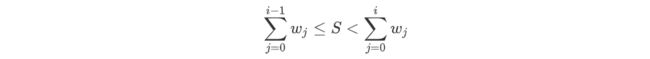
   对应的边就是被采样的边。

这个算法的问题是，如果边的数量非常大，则时间代价会很大。
论文还提出可以用alias table来解决，其采样边的时间复杂度会变成$O(1)$。

more information about alias table: https://blog.csdn.net/haolexiao/article/details/65157026

总而言之，边采样的策略能够在不改变目标函数的情况下，提高随机梯度下降的效率，且不会影响最优化结果。

其他问题

低度数顶点

对于一些顶点由于其邻接点非常少会导致embedding向量的学习不充分，论文提到可以利用邻居的邻居构造样本进行学习。

新加入顶点

对于新加入graph的node $i$，如果它跟图中的node有链接，我们可以根据目标函数$O_1，O_2$分别计算他们的一阶和二阶的embedding：

在优化过程中，已有顶点的embedding 保持不变，仅更新新顶点的embedding。

如果顶点$i$不与其他顶点相连，则需要借助其他信息（这也是alibaba 2018年的论文解决的问题）。