Yolo系列知识点梳理（Yolov1-v5）

1 概述

Yolo系列的模型是大多数做目标检测的图像算法工程师都在使用的，使用时经常也是先用了看看效果再说，如果效果不错，有时间再回头来研究一下模型，有时甚至就忘了回过头来细究。这篇文章就是一个回头的产物。

Yolo的每一个系列都令人惊艳，本文综合了原始论文和网上各家的一些说法，把Yolo每个系列究竟产出了一些什么做一个系统的梳理，也方便我以后的再回头。

如果Yolo之后有人继续更新下去，本文也会尽量做到继续更新。

文中的图片都出自参考资料，非本人原创。

2 Yolo系列模型

2.1 基石 - Yolov1

Yolov1是目标检测中one-stage方法的开山之作，它不同于two-stage需要先过一个RPN网络得到候选区域的方法，yolo直接在整张图的feature map上进行目标的定位和分类，因此速度也比当时正红的Fast R-CNN快很多。而且，也正是因为yolo看的是全局的信息，yolo把背景误判成目标的错误率比只看proposals的Fast R-CNN低很多。不过整体的准确率，还是Fast R-CNN高。

2.1.1 Yolov1的网络结构

Yolov1的网络结构如下图所示，并不复杂，输入是$448\times 448\times 3$的图片，输出是一个$7\times 7\times 30$的feature map。网络中共有24个全卷积和尾部的2个全连接，其中用到了大量的$1\times 1$卷积用来改变通道数，当然也有融合通道之间特征的作用。这里最后用的两层全连接其实今天看来有点不解，后面的版本就没有用了。这个网络结构就是大名鼎鼎的Darknet。

图1 Yolov1网络结构示意图

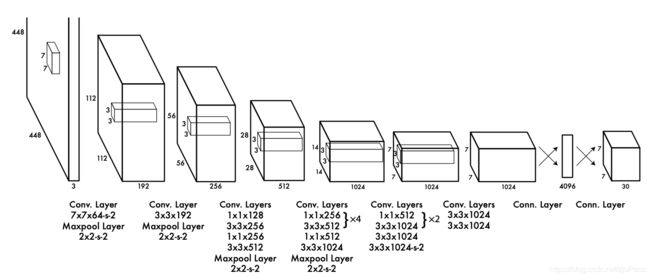
网络的卷积层在ImageNet上用分类任务进行了预训练，使得卷积层可以抽到比较好的图像特征，但是预训练时的输入图像为$224\times 224$的，这其实会有点问题，在训练检测模型时，输入为$448\times 448$，模型需要去适应这种分辨率的转换，对结果是有影响的，这个在之后的版本会优化。

2.1.2 Yolov1的feature map

我们再来看下Yolov1输出的$7\times 7\times 30$的feature map，其中$7\times 7$是经过层层全卷积和全连接之后下采样得到的结果，每个grid对应着原图上相应位置的一块区域，可以理解为将$448\times 448$的输入长宽都等分为了7份，共有49个grids。

每个grid都对应了一个长度为30的向量，准确来说应该是一个$2\times 5+20$的向量，其中2表示2个预测框；5表示每个预测框的$[x_{center},y_{center},w,h,confidence]$，$confidence$指的是这个预测框内目标的置信度$Pr(Object)\times IO{U}_{pred}^{truth}$，当没有物体时，$Pr(Object)=0$，$confidence=0$，当有物体时，$confidence=IO{U}_{pred}^{truth}$；20表示20种目标类别的置信度，表示为$Pr(Clas{s}_i|Object)$。

在预测时，最终某个框内表示了某个目标的置信度为$confidence\times Pr(Clas{s}_i|Object)$。

图2 Yolov1的feature map示意图

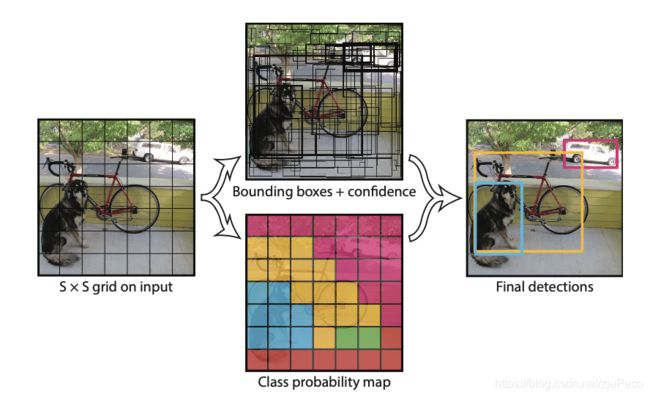
写一个一目了然版的就是某个grid的30维向量为
$$[x_{c1},y_{c1},w_1,h_1,confidenc{e}_1,x_{c2},y_{c2},w_2,h_2,confidenc{e}_2,cat{e}_1,...,cat{e}_{20}]$$

如果要知道某个grid第一个框表示$cat{e}_1$这个目标的概率，则为$confidenc{e}_1\times cat{e}_1$。

仔细一想，会发现每个grid只能表示一个物体，$confidenc{e}_i$代表了有没有物体和用哪个预测框，$cat{e}_i$表示了这个物体是哪个目标类别。也就是$7\times 7$的feature map最多只能预测出49个目标，这对小目标和相邻多目标很不友好。

2.1.3 Yolov1的训练

训练部分只讲和loss相关的内容，其他的和Yolo本身关系不大，都是标准的pipeline。

训练时，我们的label是每张图片多个检测框坐标和对应的物体类别。每个物体都会落在$7\times 7$的feature map中的某一个格子里，落到哪个格子里，那么那个格子里就负责预测这个物体。而每个格子又有两个框，就取其中和真实物体的bbox的iou较大的那个预测框作为负责这个物体的预测框。这里负责的意思就是算loss的时候拿负责的框去算loss。

loss共由五个部分组成：
（1）中心定位误差

就是负责这个物体的检测框的中心点坐标和这个物体真实的中心点坐标差多少。

$$L_1=\sum _{i=0}^{S^2}\sum _{j=0}^B{\mathbb{I}}_{ij}^{obj}((x_i-{\hat{x}}_i{)}^2+(y_i-{\hat{y}}_i{)}^2)\text{\hspace{1em}(2-1)}$$

其中，$S^2$表示$7\times 7$的feature map的格子的集合；$B$表示每个格子中bbox的集合；${\mathbb{I}}_{ij}^{obj}$是一个指示函数，表示第$i$个格子的第$j$个框负责预测真实物体时进行后面的计算，否则为0；$x_i$和$y_i$是ground truth的中心点坐标；${\hat{x}}_i$和${\hat{y}}_i$是负责这个物体的预测框的中心坐标。

（2）宽高误差

就是负责这个物体的检测框的宽高和这个物体真实的宽高差多少。

$$L_2=\sum _{i=0}^{S^2}\sum _{j=0}^B{\mathbb{I}}_{ij}^{obj}((\sqrt{w_i}-\sqrt{{\hat{w}}_i}{)}^2+(\sqrt{h_i}-\sqrt{{\hat{h}}_i}{)}^2)\text{\hspace{1em}(2-2)}$$

其中，$w_i$和$h_i$是ground truth的宽高；${\hat{w}}_i$和${\hat{h}}_i$是负责这个物体的预测框的宽高。其他符号和$L_1$中相同。

（3）正样本confidence误差

保证负责物体的预测框的confidence接近1。

$$L_3=\sum _{i=0}^{S^2}\sum _{j=0}^B{\mathbb{I}}_{ij}^{obj}(C_i-{\hat{C}}_i{)}^2\text{\hspace{1em}(2-3)}$$

其中，$C_i$表示这个格子内有物体中心的标签，${\hat{C}}_i$表示这个格子内有物体中心的置信度。

（4）负样本confidence误差

保证不负责物体的预测框的confidence接近0。

$$L_4=\sum _{i=0}^{S^2}\sum _{j=0}^B{\mathbb{I}}_{ij}^{noobj}(C_i-{\hat{C}}_i{)}^2\text{\hspace{1em}(2-4)}$$

其中，${\mathbb{I}}_{ij}^{noobj}$是一个指示函数，表示第$i$个格子的第$j$个框不负责预测真实物体时进行后面的计算，否则为0。

（5）类别误差

表示负责预测的格子内的类别误差。

$$L_5=\sum _{i=0}^{S^2}{\mathbb{I}}_i^{obj}\sum _{c\in classes}(p_i(c)-{\hat{p}}_i(c){)}^2\text{\hspace{1em}(2-5)}$$

其中，${\mathbb{I}}_i^{obj}$是一个指示函数，表示第$i$个格子的负责预测真实物体时进行后面的计算，否则为0；$p_i(c)$表示第$i$个格子第$c$个类别的标签；${\hat{p}}_i(c)$表示第$i$个格子第$c$个类别的置信度。

综合，$(2-1)-(2-5)$就有

$$L={\lambda }_{coord}{L}_1+{\lambda }_{coord}{L}_2+L_3+{\lambda }_{noobj}{L}_4+L_5\text{\hspace{1em}(2-6)}$$

其中，${\lambda }_{coord}$和${\lambda }_{noobj}$是可以用来调整的超参数，也就是各个loss的权重。不难看出Yolov1把目标检测看成了一个回归问题。

2.1.4 Yolov1的预测

预测部分没啥说的，就是对得到的98个预测框进行一个阈值的筛选之后，再做nms。

2.1.5 Yolov1小结

优点：
（1）速度快
（2）考虑图片的全局特征，precision较高

缺点：
（1）每个格子只能预测一个物体，对密集型的物体检测不友好
（2）下采样次数多，最终所使用的特征比较粗糙

2.2 Yolo9000 - Yolov2

Yolov2在Yolov1的基础上有很大的改动，这一节就针对改进部分依次说明。

2.2.1 Better

2.2.1.1 引入了Batch normalization

BN是一个非常有用的模块，其有点如下：

• 加快收敛
• 改善梯度，远离饱和区
• 允许大的学习率
• 对初始化不敏感
• 相当于正则化，使得有BN层的输入都有相近的分布

有了BN之后，就可以不用dropout了，或者说不能像原来一样用dropout了，这会导致训练和测试的方差偏移，可以参看文献[5]。

2.2.1.2 高分辨率的分类器

Yolov1当中对backbone做预训练的时候，用的是$224\times 224$的输入，而yolov1为了高分辨率用的是$448\times 448$的输入，这样就导致了模型要去适应这个分辨率的转换。于是，Yolov2干脆直接用$448\times 448$的输入预训练backbone了。这样带来了几乎4%mAP的提升。这种简单而高效且不用增加预测负担的方法是我们最喜欢的。

2.2.1.3 加入了anchor机制

在Yolov1中没有anchor的概念，所以$7\times 7$的feature map中预测的两个预测框都是野蛮生长的，这两个预测框很有可能就长的差不多，而且这样去学习不同形状的物体，对模型来说是比较困难的。

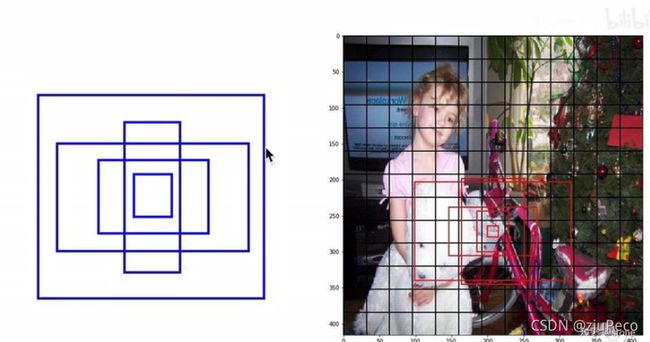
所以，Yolov2删去了最后的全连接层，引入了anchor机制。Yolov2的输入变成了$416\times 416$，feature map大小为$13\times 13$，每个格子有5个anchors，每个anchor的长宽大小和比例不同，各司其职，负责不同形状的物体。有了anchor之后，模型就不需要直接去预测物体框的长宽了，只需要预测偏移量就可以了，这相对来说降低了难度。

这里提一句，之所以从$448\times 448$变成$416\times 416$就是为的使得feature map的size是一个奇数。这样的好处是，许多图片的中心点都是某个物体的中心，奇数保证中间是一个格子，而不是偶数那样四个格子抢占中心点。

图3 Yolov2的anchor形状示意图

不过引入anchor也有不好的地方，本来不用anchor的时候，预测出来只有98个框，现在有845个框了，从最终结果来看，precision略有下降了，不过recall变高了许多。

图4 Yolov2的anchor输出示意图

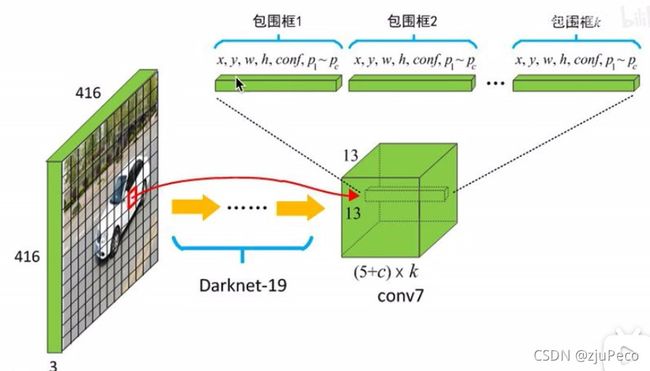
Yolov1的输出是一个$7\times 7\times 30$的，Yolov2的输出是一个$13\times 13\times 125$，其中$125=(5+20)\times 5$。括号里的$5$表示$x_i,y_i,w_i,h_i,con{f}_i$,$20$表示每个类别的概率，共20个类别，最后的$5$表示$5$个预测框。图4表示的非常清楚了。

可以看出，同一个格子里的每个预测框的类别是可以不同的，一个格子可以预测5个物体了。

图5 Yolov2的anchor聚类示意图

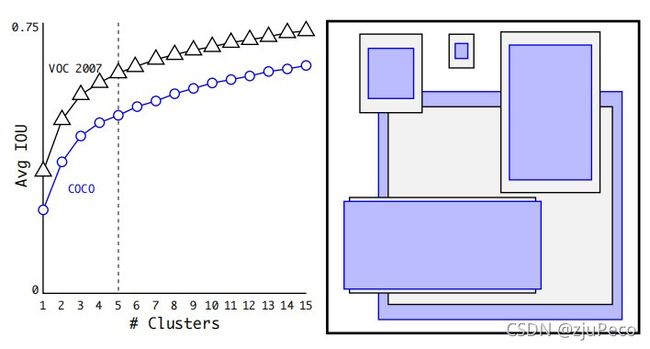
那么这5个anchor的预锚框是怎么确定的呢？甚至为什么是5个呢？根据论文中所述，anchor的形状是在VOC 2007和COCO数据集上聚类得到的，聚类的类别个数从1到15都试过，最终在效果和性能的权衡之下选择了5个类聚出来的锚框形状，示意图如上图5所示。

图6 Yolov2的anchor编码示意图

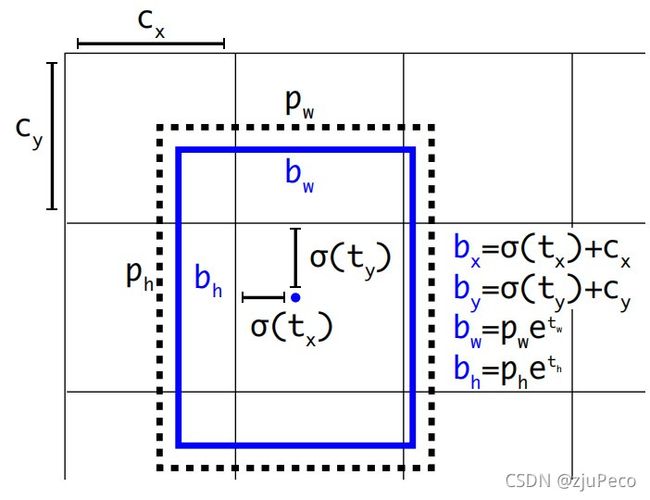
说了半天，模型究竟是怎么计算offset的呢？如上图6所示，yolov2的anchor编码在二阶段的检测模型的基础上做了改进。图6中$c_x$和$c_y$是每个格子的左上角坐标，$t_x$和$t_y$是模型预测锚框中心点坐标时的输出参数，加了$\sigma$就把中心点的偏移量限定在了这个格子里，这样不管模型怎么预测，中心点都飞不出这个格子。$p_w$和$p_h$是预锚框的初始宽高，$t_w$和$t_h$是模型预测锚框宽高的输出参数，这里就没有限制最终锚框的形状。$b_x$，$b_y$，$b_w$，$b_h$是最终的预测框的中心点坐标和宽高。我把图中的公式抄一份下来就是$(2-7)$。

$$\begin{array}{rl}{b}_x& =\sigma (t_x)+c_x\\ b_y& =\sigma (t_y)+c_y\\ b_w& =p_w{e}^{t_w}\\ b_h& =p_h{e}^{t_h}\end{array}\text{\hspace{1em}(2-7)}$$

除此之外，还有一个东西叫做$t_o$，$t_o$是用来给出有物体的置信度的。

$$P_r(object)IOU(b,object)=\sigma (t_o)\text{\hspace{1em}(2-8)}$$

2.2.1.4 loss的改动

Yolov2的loss我直接拿子豪兄做的图了，这个也是网友们根据源码整理出来的，论文中并没有说这件事。

图7 Yolov2的loss示意图

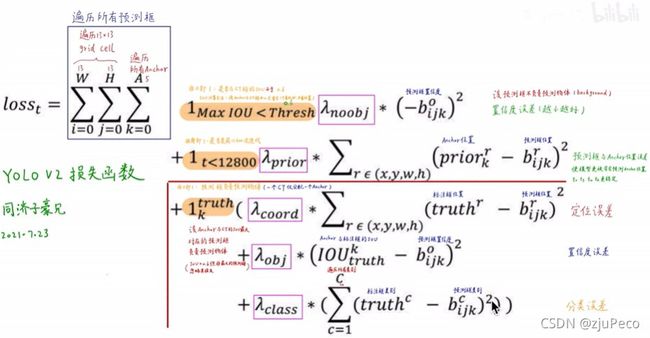
前面的三个求和就是指的下面的所有操作都是对每个格子每个预测框分别做的；${\mathbb{I}}_{MaxIOU<Thresh}$表示845个框分别和所有的ground truth求IOU，如果最大的IOU也小于阈值Thresh的话，就认为这个框是背景，其输出的置信度$b_{ijk}^o$要越小越好；${\mathbb{I}}_{t<12800}$表示前12800次迭代，也就是模型训练的早期时候，这里让模型的预测锚框接近预锚框，有点先重置一下的意思，不让初始的锚框太横七竖八；${\mathbb{I}}_k^{truth}$表示对负责预测ground truth的锚框进行的loss计算。所有的Loss也都是回归运算。

2.2.1.5 Fine-Grained Features

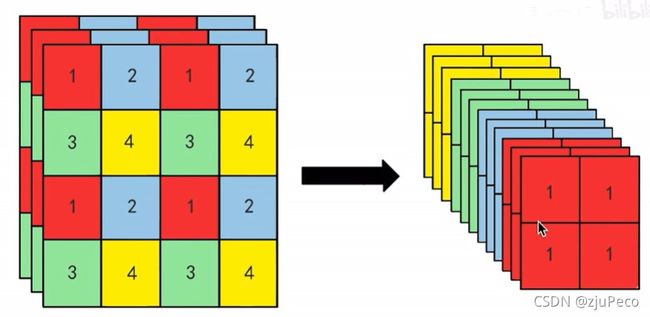
增加了细粒度的特征，方法就是把浅层的$26\times 26\times 512$这层的输出分成四份之后concat到原来的特征上。$26\times 26\times 512$分成四份并concat就变成了$13\times 13\times 2048$，这个和$13\times 13\times 1024$的特征concat到一起变成了$13\times 13\times 3072$。

图8 Yolov2的pass through示意图

四分的方式有点空洞卷积的意思，如下图9所示。

图9 Yolov2的pass through切分方式示意图

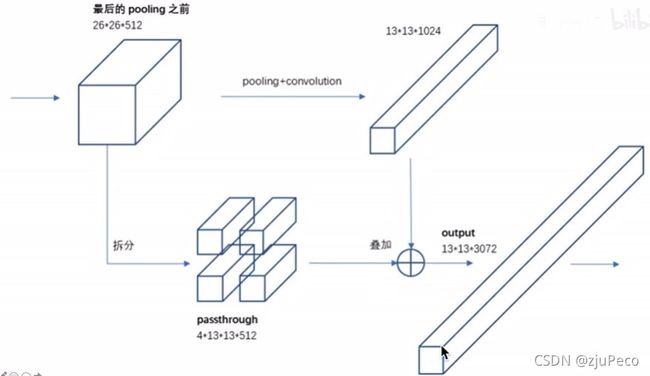
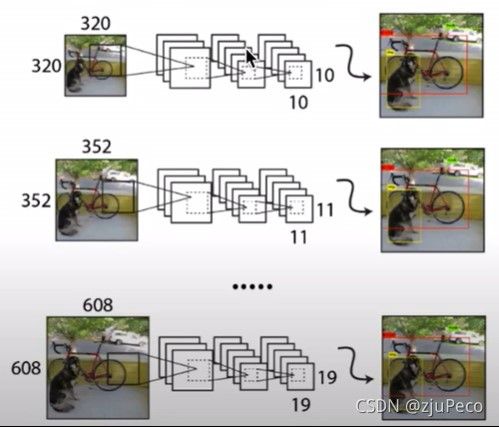
2.2.1.6 多尺度训练

Yolov2每10个batches就会换一下输入的尺度，使得模型泛化于不同尺度的输入，这得益于adaptive pooling层。高分辨率的输入速度慢，但是对小目标的检测效果要好很多，低分辨率的输入速度快。

图10 Yolov2的多尺度训练示意图

2.2.2 Faster

这部分没啥说的，就是把backbone给换成了Darknet-19，都是卷积层和pooling层，更加轻量了。

2.2.3 Stronger

这部分是作者对超多分类的一次尝试，但估计效果没有那么好，只是一个设想。

用来训练检测模型的数据集coco有80个类别，10万的图片，但用来分类的数据集imagenet有22k个类别，140万的数据。作者想要把imagenet的数据和类别拿来用，于是就相处了层级分类这个办法，如下图11所示。

图11 Yolov2的层级分类示意图

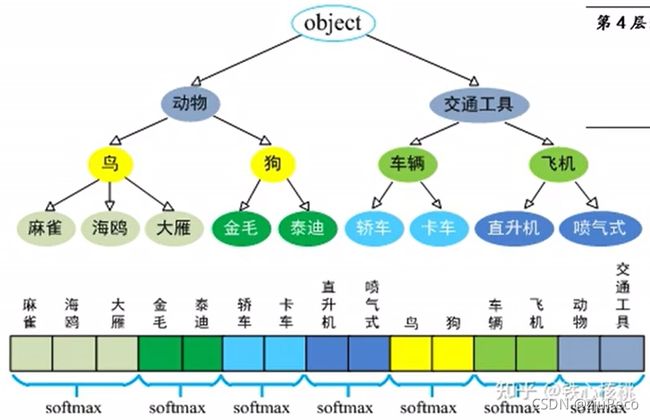
imagenet中的每个类别并不是完全两两互斥的，它们之间是有层级关系的，所以作者借助wordnet把类别进行了分层，同一层的类别分别进行softmax，这样就做到了多层级的分类。检测模型的类别都是包含在这些类别之中的，再将其应用到检测模型即可。

这只是一个设想，了解一下即可。

2.3 一小步 - Yolov3

Yolov3相对于Yolov2没有太多大的改进，用作者的话说就是"I managed to make some improvements to YOLO. But, honestly, nothing like super interesting, just a bunch of small changes that make it better."

作者对backbone的网络结构进行了改进，将Darknet19结合Resnet，变成了Darknet53。作者把残差块轻量化了一下，如下图12所示。

图12 Yolov3的残差块轻量化示意图

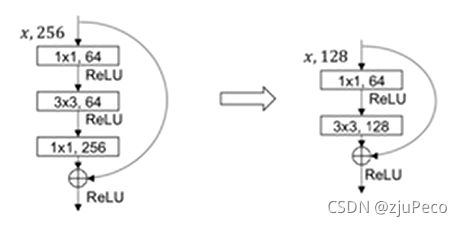
除此之外，还增加了多尺度训练机制，增加了多尺度训练的网络结构示意图如下图13所示。输出三个尺寸的feature map，分别是$13\times 13$，$26\times 26$和$52\times 52$。大尺寸的feature map是小尺寸的feature map上采样并结合浅层特征得到的。

图13 Yolov3的网络结构示意图

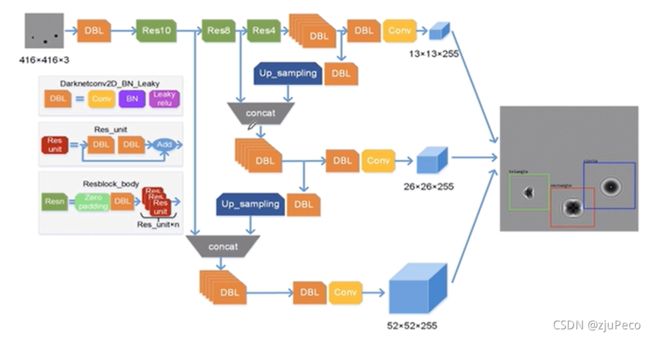
每个尺寸的feature map各司其职，$13\times 13$负责大目标物体，$26\times 26$负责中目标物体和$52\times 52$负责小目标物体。原因很简单，越深层的信息越抽象，越浅层的越粗糙，浅层还保留着小物体的信息，深层就不一定还在了。

从图13中可以看到feautre map的输出channel变成了256，这个是因为Yolov3的anchor变成了9个，每个尺度的feature map有3个，然后类别变成了80类，所以每个尺度的feature map有$256=3\times (4+1+80)$。

图14 Yolov3的多尺度示意图

Yolov3就这些重要的改进。

2.4 技巧 - Yolov4

Yolov4可以说是目标检测各种小技巧的大总结，它将技巧分为了bag of freebies(BoF)和bag of specials(BoS)两种，BoF指的是只增加训练的成本而不增加推理的成本的技巧，通常是前后处理；BoS指的是只增加一点推理成本却可以显著提高模型效果的技巧，通常是结构上的变化。

不同的BoF和BoS面对不同的问题和数据集有不同的效果，根据需求选择即可。

BoF和BoS都有一大堆，要在这里全讲完太费时间，也与这篇文章的目的相悖。这里只讲一些重要的，且最终的Yolov4用上的技巧。下图15是Yolov4真正用到的一些改进。

图15 Yolov5的技巧选择示意图

这里不会把上面的所有改进都讲了，只挑一些重要的讲。

2.4.1 网络结构的改进

2.4.1.1 backbone中的激活函数改为Mish

Yolov3中的卷积快都是CBL的结构，Yolov4改成了CBM，也就是把激活函数给改成了Mish，其示意图如下图16所示。

图16 CBL变为CBM示意图

Leaky Relu激活函数是（$a$是很小的常数）

$$f(x)=\{\begin{array}{ll}ax,& ifx<0\\ x,& otherwise\end{array}\text{\hspace{1em}(2-9)}$$

Mish激活函数就是

$$f(x)=x\cdot tanh(log(1+e^x))\text{\hspace{1em}(2-10)}$$

这里顺便来说说常用的激活函数的优缺点。

sigmoid两端很容易饱和，会造成梯度消失的问题，中间梯度很大，会造成梯度爆炸问题。用sigmoid做激活函数，神经网络不太好训练。但是sigmoid的非线性表达能力很强，因为它不管怎么高阶求导仍旧是非线性的。

tanh和sigmoid很像，不过它是以0为中心。

relu的问题是，它的负半轴没梯度了，正半轴求个导是常数，非线性表达能力很弱。但是它快。所以用relu的网络一般网络层数很深，以此来弥补relu非线性能力表达弱的缺陷。

leaky relu负半轴做了优化，但还是非线性表达能力弱。

mish结合了relu和tanh的优点。它无上限，这样可以保证没有饱和区域，不会梯度消失。有下限，能够保证具有一定的正则能力。同时非线性表达能力也不错。

2.4.1.2 backbone中的残差模块改成了CSP

Yolov3中的残差模块如下图17所示，resX中的X表示的是有X个Res unit。

图17 Yolov3残差模块示意图

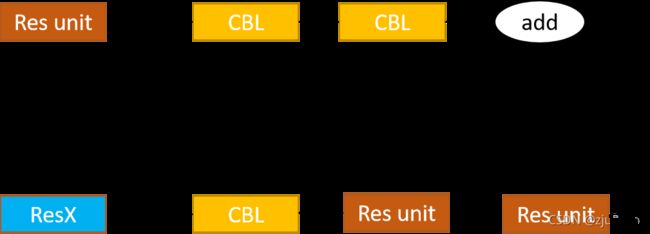
Yolov4则是将残差模块替换为了CSP模块，如下图18所示，其中的CSPX中的X表示有X个Res unit。

图18 Yolov4残差模块示意图

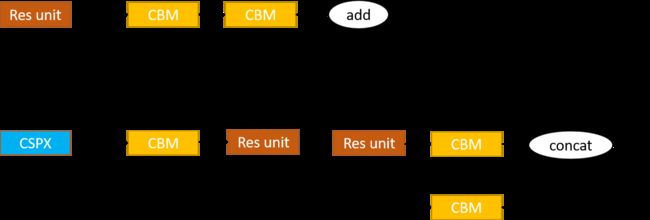
可以看出CSPX效仿残差块，额外加了一路，并且这一路中多了一个CBM，最后的add也变成了concat。相当于一堆残差的外面再残差了一遍。这里加个CBM直观上是为了改变特征的shape，使其可以顺利concat。除此之外，资料[8]中的猜想是，这是为了平衡上下两路的信息，相当于加了个电阻。每个这个电阻，就是个短路的状态，信息都从下面走了，有了这个电阻，就可以尽可能平衡上下路的信息。这只是个猜想。

2.4.1.3 detector中的新增了SPP模块

SPP的作用是增大感受野。它很简单，就是一堆MaxPooling，每个MaxPooling的kernel size大小不同，就有不同感受野的结果，最后再全都concat起来即可，其示意图如下图19所示。

图19 Yolov4的SPP示意图

SPP之所以不放在backbone是因为这会造成大量的信息丢失，而放在detector里却起到了降维的作用。

2.4.1.4 detector中特征尺度的变化

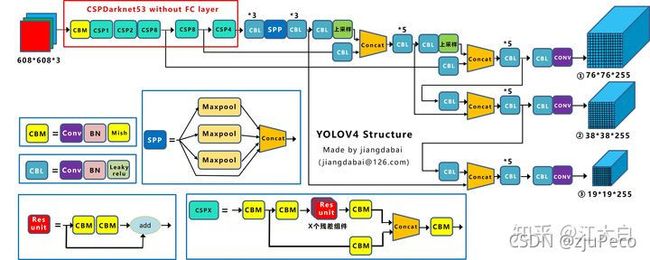
Yolov4还读detector中的尺度特征做了很大的修改，如下图20和图21分别是yolov3和yolov4的网络结构图。

图20 Yolov3网络结构图

图21 Yolov4网络结构图

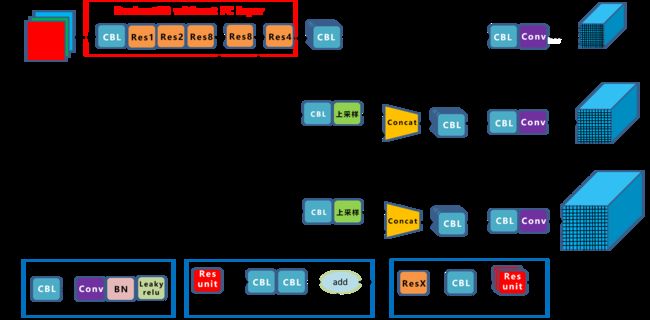
不难看出Yolov3是$19\times 19$ -> $38\times 38$ -> $76\times 76$的，而Yolov4是反过来的，这主要是为了增加特征融合性，也就是feature map中融合了更多层的信息。特别是$19\times 19$这个feature map，融合的特征最多了，也就是对大目标的检测效果更好了。应该说不管大小目标，总体都有提升。

2.4.2 损失函数的改进

（1）变为smoth_L1
之前Yolo的损失函数当中有大量的L2损失，在Yolov4中改成了smooth L1。smooth L1结合了L1和L2损失的优点。先来看下L1和L2损失的公式

$$\begin{gathered} L1=\frac{1}{n}\sum _{i=1}^n|f(x_i-y_i)| \\ L2=\frac{1}{n}\sum _{i=1}^n(f(x_i)-y_i{)}^2\text{\hspace{1em}(2-11)} \end{gathered}$$

L1的优点是倒数很稳定，但是是一个阶段函数，在$(0,0)$处是一个折线。L2的优点是在$(0,0)$处是可导的，但是离$(0,0)$越远，导数越大，会产生爆炸。所以就有了结合L1和L2的smooth L1出现

$$smoothL1=\{\begin{array}{ll}0.5x^2& if|x|<1\\ |x|-0.5& otherwise\end{array}\text{\hspace{1em}(2-12)}$$

（2）iou loss改进
这里主要参考了文献[10]

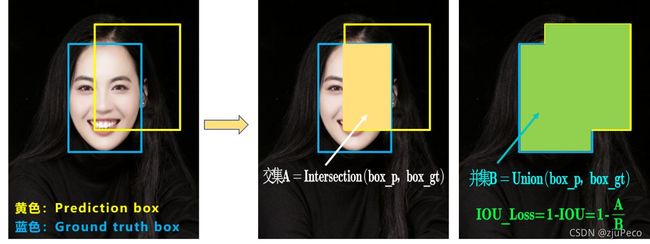
在Yolov3中的IOU loss就直接是$(1-IOU{)}^2$。这里的iou就是交集比上并集，如下图22所示。

图22 iou示意图

这里的IOU的计算方法优点缺点，且看下图23。缺点一就是左图所示，当预测框与真实框完全没有交叠时，不管预测框离真实框多远，IOU都是一样的，但其实离真实框近的比离真实框远的要好一些。缺点二就是中图和右图所示，当交集和并集一致时，不同方向的预测框得到的iou是一样的，但其实右图比中图要好一点，因为中图的中心点对齐需要预测框的水平和垂直都发生比较大的变化，而右图只需要水平平移即可。

图23 IOU缺点

为了解决上述的两个缺点，有了GIOU，如图24所示。

图24 GIOU示意图

GIOU的公式为

$$GIOU=IOU-差集/最小外接矩形\text{\hspace{1em}(2-13)}$$

最小外接矩形和差集的意思就是图24中的左图和中图，不难看初，刚才提到的两个缺点在这里已经解决了。不过还有一个问题，如图25所示。

图25 GIOU缺点

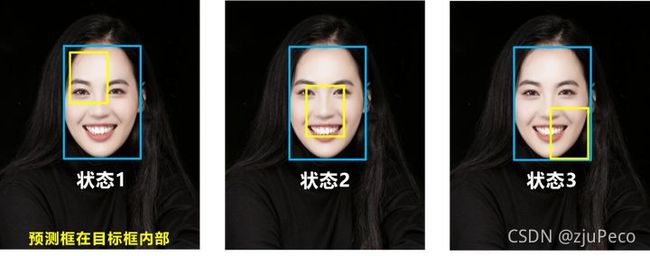
当预测框在真实框内部的时候，不管预测框在那个位置，GIOU都是一样的，但是图25的中图显然是优于左图和右图的，因为中图的水平和垂直方向的坐标已经对齐了，只需要改变长宽即可。

这个时候，就又出现了一种DIOU，如图26所示。

图26 DIOU示意图

DIOU的公式为

$$DIOU=IOU-(Distance\_2)/(Distance\_C)\text{\hspace{1em}(2-14)}$$

其中，$Distance\_C$是最小外接矩形的对角线距离，$Distance\_2$是预测框和真实框中心点的欧氏距离。

这样一来就解决了图25的缺点。但是，别急，还有一个缺点。DIOU没有考虑长宽比。

图27 DIOU缺点

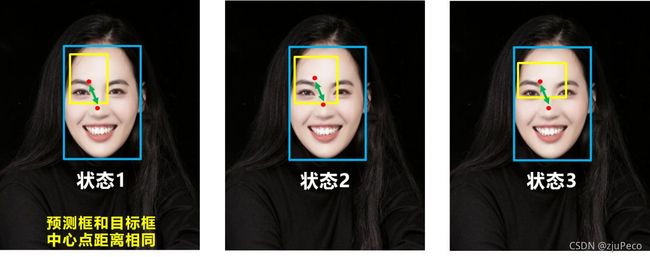
图27中当预测中心点距离真实中心点一样时，预测框的长宽比与真实框接近的，显然是更优的。于是，就有了终极版的CIOU。

CIOU的公式为

$$CIOU=IOU-\frac{Distance\_2^2}{Distance\_C^2}-\frac{v^2}{1-IOU+v}\text{\hspace{1em}(2-15)}$$

其中，$v$是长宽比的一致性参数，定义为

$$v=\frac{4}{\pi }(arctan\frac{w_{gt}}{h_{gt}}-arctan\frac{w_{pred}}{h_{pred}}{)}^2\text{\hspace{1em}(2-16)}$$

至此，iou经历了这么多版本，最终确定为CIOU。

2.4.3 nms的改进

在训练的时候用的是CIOU，但是在做nms的时候，用了diou-nms。用diou-nms可以把一些重叠度很高的框，但表示不同物体的给保留下来。至于为什么不用CIOU，我觉得是没有必要，且会增加计算复杂度。我不太同意文献[10]中说的CIOU在做nms时没有真实框，$v$没法计算的说法，两个框做对比，把置信度高的当成真实框即可。

2.4.4 其他

其他比较重要的可能就是cutout，mosaic之类的数据增强的方法了，这个这里就不细讲了。

2.5 又一小步 - Yolov5

Yolov5和Yolov4差不多可以说没有做太多的改进，不过工程上更友好了一些，使用起来也更加方便。

2.5.1 网络结构的改进

2.5.1.1 添加了CSP2模块

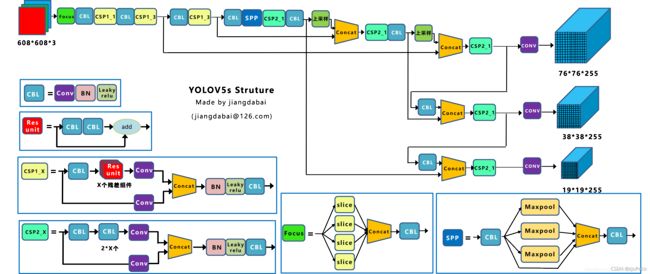
下图28时Yolov5的网络结构图，和Yolov4几乎时一摸一样，做了一点点改进。

（1）把CBM换回了CBL，可能是为了提升速度。
（2）设计了CSP2模块，如图28的左下角所示，就是把之前CSP中的残差块改成了CBL。
（3）添加了Focus模块。这个其实就是Yolov2中的pass through。

图28 Yolov5网络结构图

2.5.2 其他

还有就是一些零零碎碎的东西，这里简单列几个比较有用的吧。

（1）添加了训练前自动计算最佳预锚框的模块。
（2）自适应图片缩放，就是padding的时候，去掉一些没用的黑边。

3 结束语

这里根据网上各家的资料总结了很多，其中也有一些自己的理解，对我自身了解Yolo有很大的帮助，也希望给看到这篇博客的人有一些帮助。

参考资料

[1] You Only Look Once: Unified, Real-Time Object Detection
[2] 【子豪兄】YOLOV1目标检测，看我就够了
[3] YOLO9000: Better, Faster, Stronger
[4] 【精读AI论文】YOLO V2目标检测算法
[5] Understanding the Disharmony between Dropout and Batch Normalization by Variance Shift
[6] YOLOv3: An Incremental Improvement
[7] YOLO系列算法之YOLOv3算法精讲
[8] 2021最新人工智能深度学习YOLOv4与YOLOv5教程
[9] YOLOv4: Optimal Speed and Accuracy of Object Detection
[10] 深入浅出Yolo系列之Yolov3&Yolov4&Yolov5&Yolox核心基础知识完整讲解
[11] 深入浅出Yolo系列之Yolov5核心基础知识完整讲解