Harris算子原理以及python实现

（一）Harris算子的实现

本系列研究的是自适应超参数估计的Harris算子
学习过程主要分为一下几部分：

• Harris算子的实现
• 学习随机过程和优化估计理论 论文研读，调研相关研究文献，了解国内外研究现状
• 采集超参数与图像局部多尺度之间的关系，并在此基础上建立统计模型，实现参数优化选择
• （时间空余情况下）学习工具matlab

---

---

前言

　特征点检测广泛应用到目标匹配，目标跟踪，三维重建等应用中，在进行目标建模时会对图像进行目标特征的提取，常用的有颜色，角点，特征点，轮廓，纹理等特征。而下面学习常用的特征点检测。 　总结一下提取特征点的作用： 1. 运动目标跟踪 2. 物体识别 3. 图像配准 4. 全景图像拼接 5. 三维重建 　而一种重要的点特征就是角点，本文就学习基于角点检测的算法：Harris角点检测

---

一、Harris算子的前身Moravec算子

$E(u,v)={\sum }_{x,y}w(x,y)[I(x+u,x+y)-I(x,y){]}^2$

• u,v - 水平、竖直方向的偏移
• x,y - 窗口的中心
• w(x,y) - 滤波函数
• I(x+u,x+y)、I(x,y) -分别为偏移点的灰度值、窗口中心点的灰度值
  
  　我们可以看到E(u,v)的值越大，越可能是角点

二、Harris算子原理实现

1.Moravec算子的不足

• 由于Moravec算子只考虑了4种方向，不具有旋转不变性，具有很大局限性，一张图片旋转个15°可能就被判定为不一样了；
  

• harris算子运用全微分、泰勒展开的思想把方向细化了，考虑了多个方向。

  公式推导：
  $E(u,v)={\sum }_{x,y}w(x,y)[I(x+u,x+y)-I(x,y){]}^2$
  $f(x+u,y+v)\approx f(x,y)+u{f}_x(x,y)+v{f}_y(x,y)$

  $⟹$
  $E(u,v)={\sum }_{x,y}w(x,y)(u^2{I}_x^2+2uv{I}_x{I}_y+v^2{I}_y^2)$

• $I_x$ - 图像的水平梯度，即I(x+u,y+v)对x求偏导

• $I_y$ - 图像的垂直梯度，即I(x+u,y+v)对y求偏导
  我们将用梯度算子Sobel来算梯度

$⟹$该公式可以进一步化为矩阵形式：
$E(u,v)=[u,v](\sum w(x,y)\left[I_x^2{I}_x{I}_y{I}_x{I}_y{I}_y^2\right])[u,v{]}^T$
这是一个22的矩阵*

$⟹$简化中间括号里的内容，公式简化为如下形式：
$E(u,v)=[u,v]M[u,v{]}^T$
这是一个二次型

2.Sobel

代码如下：

Dx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=ksize)
Dy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=ksize)

3.角点响应

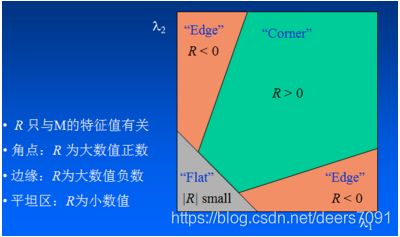
　 　M为梯度的协方差矩阵，在实际应用中为了能够应用更好的编程，定义了角点响应函数R，通过判断R大小来判断像素是否为角点。
　 　R取决于M的特征值，对于角点 |R| 很大，平坦的区域 |R| 很小，边缘的 R 为负值。
　 　当然，这样计算量非常大，因为图像中的几乎每个点都需要进行一次特征值的计算，下面给出一个角点响应函数R的经验公式：
　 　 　$R=detM-\alpha (traceM)$
　 　 　$detM$表示M的行列式，$traceM$表示M的迹，R表示角点响应值，$\alpha$表示经验常数，一般在0.04~0.06之间取值。
　 　判断准则：当R超过某个设定的阈值时，可认为是角点，反之，则不是。

4.Harris算子的python实现

核心函数实现：

1. 计算图像两个方向的梯度（Sobel）
2. 滤波
3. 遍历边缘图像中的像素点
   计算当前点的角点响应值R
4. 返回R矩阵

代码如下（示例）：

import numpy as np
import cv2

#blocksize窗口大小；
#ksize算梯度的时候用的那个东西的大小，这里用的sobel是3*3
def cornerHarris(img, blocksize=2, ksize=3, k=0.04):
    #下面是一个闭包
    def _clacHarris(cov, k):
        #numpy.zeros
        #创建指定大小的数组，数组元素以 0 来填充：
        result = np.zeros([cov.shape[0], cov.shape[1]], dtype=np.float32)
        for i in range(cov.shape[0]):
            for j in range(cov.shape[1]):
                a = cov[i, j, 0]
                b = cov[i, j, 1]
                c = cov[i, j, 2]
                result[i, j] = a*c-b*b-k*(a+c)*(a+c)
        return result

    #算图像竖直和水平方向的梯度
    Dx = cv2.Sobel(img, cv2.CV_32F, 1, 0, ksize=ksize)
    Dy = cv2.Sobel(img, cv2.CV_32F, 0, 1, ksize=ksize)

    #img.shape 图像数组的大小（行、列、颜色通道）
    cov = np.zeros([img.shape[0], img.shape[1], 3], dtype=np.float32)

    for i in range(img.shape[0]):
        for j in range(img.shape[1]):
            cov[i, j, 0] = Dx[i, j]*Dx[i, j]
            cov[i, j, 1] = Dy[i, j]*Dy[i, j]

    #算块内的梯度和w（x，y）,boxFilter换成高斯效果会好一点
    #cov = cv2.boxFilter(cov, -1, (blocksize, blocksize), normalize=False)
    #高斯滤波
    cov = cv2.GaussianBlur(cov, (9, 9), 0)


    return _clacHarris(cov, k)


if __name__ == '__main__':
    img = cv2.imread('test1.png')
    # 最近邻插值法缩放
    # 缩放到原来的四分之一
    img = cv2.resize(img, (0, 0), fx=0.5, fy=0.5, interpolation=cv2.INTER_NEAREST)
    gray_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)#把RGB图转成灰度图
    result = cornerHarris(gray_img, 2, 3, 0.04)
    #角点检测
    pos = cv2.goodFeaturesToTrack(image=result, maxCorners=1000, qualityLevel=0.1, minDistance=1, useHarrisDetector=True, k=0.04)
    for i in range(len(pos)):
        #根据给定的圆心和半径等画圆cv2.circle(img, center, radius, color[, thickness[, lineType[, shift]]])
        cv2.circle(img=img, center=(pos[i][0][0], pos[i][0][1]), radius=2, color=[0, 0, 255], thickness=3)

    cv2.imshow('harris', img)
    cv2.waitKey(0)

效果：

---

总结

　 　该篇只是简单讲解了harris算子的原理以及实现，对于涉及到的Sobel函数、滤波函数、高斯函数原理都未详细涉及，后续会补充。

参考链接: OpenCV计算机视觉学习（13）——图像特征点检测（Harris角点检测，sift算法）.