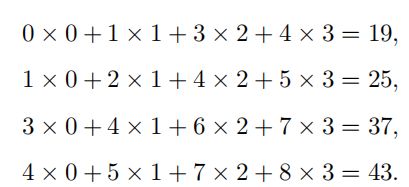读书笔记-卷积神经网络

1. 从全连接层到卷积

因为我们遵循平移不变形和局部性，所以我们在全连接层的基础上形成了卷积神经网络，故卷积神经网络是一种特殊的全连接层。

1.1 平移不变性

不管检测对象出现在图像的哪个位置，神经网络的前几层应该对相同的图像区域具有相似的反应。
我们定义两个变量：

• $[X{]}_{i,j}$:表示输入图像的中位置 (i,j) 的像素
• $[H{]}_{i,j}$:表示隐藏的中位置 (i,j) 的像素
  为了使每个隐藏神经元都能接收到每个输⼊像素的信息，我们将参数从权重矩阵（如同我们先前在多层感知机中所做的那样）替换为四阶权重张量 W。假设 U 包含偏置参数，我们可以将全连接层形式化地表⽰为：
  $$[H{]}_{i,j}=[U{]}_{i,j}+\sum _k\sum _l[W{]}_{i,j,k,l}[X{]}_{k,l}\text{\hspace{1em}(1)}$$
  $$[H{]}_{i,j}=[U{]}_{i,j}+\sum _a\sum _b[V{]}_{i,j,a,b}[X{]}_{i+a,j+b}\text{\hspace{1em}(2)}$$
  从 W到V之间的转换只是形式的转换，因为在这两个四阶张量的元素之间存在一一对应的关系，我们只需重新索引下标(k,l);k=i+a;l=j+b;因此可得如下：
  $$[V{]}_{i,j,a,b}=[W{]}_{i,j,i+a,j+b}\text{\hspace{1em}(3)}$$
  索引 a,b 通过在正偏移和负偏移之间移动覆盖整个图像。对于隐藏表示中任意给定位置 (i,j)处的像素值 $[H{]}_{i,j}$,可以通过在 x 中以 (i,j) 为中心对像素进行加权求和得到，加权使用的权重为$[V{]}_{i,j,a,b}$,平移不变性指的是在检测对象在输入 X 中的平移，应该仅仅导致隐藏表示 H中的平移。也就是 U 和 V实际上不依赖 i,j 的值。数学可表达为：
  $$[V{]}_{i,j,a,b}=[V{]}_{a,b}\text{\hspace{1em}(4)}$$
  其中 U 可以看作是常数 u.则可以表示如下：
  $$[H{]}_{i,j}=u+\sum _a\sum _b[V{]}_{a,b}[X{]}_{i+a,j+b}\text{\hspace{1em}(5)}$$
  上述为卷积，表示的是使用系数$[V{]}_{a,b}$对位置 [i,j] 附近的像素(i+a,j+b)进行加权得到 $[H{]}_{i,j}$。因为卷积考虑到局部性和平移不变性，所以参数表示上小了很多，是巨大的进步，但是其本质上还是来自全连接层。

1.2 局部性

局部性指的是我们卷积只对局部部分进行加权计算，而不考虑局部以外的值。假设局部区间为△，我们希望：$|a|>△$或者$|b|>△$时，其训练参数 $[V{]}_{a,b}=0$,故卷积层表示如下：
$$[H{]}_{i,j}=u+\sum _{a=-△}^{△}\sum _{b=-△}^{△}[V{]}_{a,b}[X{]}_{i+a,j+b}\text{\hspace{1em}(6)}$$

2. 图像卷积

2.1 卷积计算图示

2.2 学习卷积核

关于卷积核的学习，详见下述链接。
深度学习到底是学习了什么？卷积核学习思考

2.3 小结

• 二维卷积层的核心计算为二维互相关计算，跟数学上的卷积计算有所差别
• 我们可以通过卷积核计算来对图像进行不同的处理，如锐化，高斯处理等
• 我们可以通过输入数据X和最终数据Y，通过深度学习来学习到卷积核的值
• 当需要检测输入特征中更广阔的区域，我们需要设计更深的网络。

3. 填充和步幅

3.1 填充

填充的意义在于，当我们的卷积核的大小大于1的时候，我们总会丢失部分的边缘像素，当神经网络比较浅的时候，我们可能看不出来。但当我们的网络非常深的时候，那么最终我们就会丢失掉很多信息，所以我们需要填充输入的矩阵。

• 填充方式，对称填充
  

如果我们添加 $p_h$行来填充(一半在顶部，一半在底部)，添加$p_w$列(一半在最左列，一半在最右列)，输出形状为：
$$(n_h-k_h+p_h+1)\times (n_w-k_w+p_w+1)\text{\hspace{1em}(7)}$$

• 注：
  $n_h:输入矩阵行数;k_h:卷积核行数;p_h：填充的行数$
  $n_w:输出矩阵列数;k_w:卷积核列数;p_w：填充的列数$

我们知道输入矩阵 X 的大小为$(n_h,n_w)$,输出矩阵 Y 的大小为$(n_h-k_h+p_h+1)\times (n_w-k_w+p_w+1)$;为了保证输出大小和输入大小不变，我们通常假设填充如下:
$$-k_h+p_h+1=0;-k_w+p_w+1=0\text{\hspace{1em}(8)}$$

• 整理可得如下：
  $$p_h=k_h-1;p_w=k_w-1\text{\hspace{1em}(9)}$$

3.2 填充 - Pytorch

• pytorch
  在 Pytorch 二维卷积 nn.Conv2d中的参数 padding 值是单边填充量，比如

conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)

那么输入矩阵 X 的填充是 顶部 1,底部 1,所以输出矩阵大小应该为
$$(n_h-k_h+2\ast p_h+1)\times (n_w-k_w+2\ast p_w+1)\text{\hspace{1em}(10)}$$
代入可得:
$$(n_h-3+2\ast 1+1)\times (n_w-3+2\ast 1+1)\text{\hspace{1em}(11)}$$
输出矩阵Y的形状如下，这样输入矩阵X和输出矩阵Y的大小不变
$$n_h\times n_w\text{\hspace{1em}(12)}$$

• 代码

# -*- coding: utf-8 -*-
# @Project: zc
# @Author: zc
# @File name: padding
# @Create time: 2021/12/4 15:56


# 1. 导入相关数据库
import torch
from torch import nn
from d2l import torch as d2l


# 2.矩阵大小计算
# 输入 conv2d: 卷积核，x :输入矩阵
# 返回 y：输出矩阵，y.shape ：输出矩阵的形状
def comp_conv2d(conv2d, x):
	# 将矩阵 x 加入批量大小和通道数：(批量大小,通道数，输入矩阵)
	x = x.reshape((1, 1) + x.shape)
	# 卷积计算
	y = conv2d(x)
	# 去掉矩阵中的 (批量大小，通道数)
	y = y.reshape(y.shape[2:])
	return y, y.shape


# 3. 定义二维卷积运算
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)

# 4. 获取卷积矩阵的填充值（padding） ,卷积核大小(kernel_size)
padding = conv2d.padding
kernel_size = conv2d.kernel_size

# 5. 初始化 x ,
x = torch.randn(8, 8)
x_shape = x.shape

# 6. 获取相关参数
n_h, n_w = x_shape[0], x_shape[1]
k_h, k_w = kernel_size[0], kernel_size[1]
p_h, p_w = padding[0], padding[1]
y_h, y_w = x_shape[0], x_shape[1]

# 7. 卷积计算，得到输出矩阵及形状
y, y_shape = comp_conv2d(conv2d, x)

# 8. 打印相关数据
print(f'x_shape={
       x_shape},kernel_size={
       kernel_size},padding={
       padding},y_shape={
       y_shape}')
print(f'{
       y_h}:(y_h)={
       n_h}:(n_h)-{
       k_h}:(k_h)+{
       2*p_h}:(2*p_h)+1')
print(f'{
       y_w}:(y_w)={
       n_w}:(n_w)-{
       k_w}:(k_w)+{
       2*p_w}:(2*p_w)+1')

• 结果

x_shape=torch.Size([8, 8]),kernel_size=(3, 3),padding=(1, 1),y_shape=torch.Size([8, 8])
8:(y_h)=8:(n_h)-3:(k_h)+2:(2*p_h)+1
8:(y_w)=8:(n_w)-3:(k_w)+2:(2*p_w)+1

3.3 步幅 stride

步幅指的是卷积核每次滑动元素的数量。步幅的作用是为了采样的压缩，以前是一步一步的移动卷积核，如果像素之间相似东西太多，我们其实没必要进行一步一步的移动采集，我们完全可以跳着采集嘛，所以一般步幅的作用为了压缩数据，步幅一般是2，比如，输入矩阵是(8,8),当我们的步幅stride = 2的时候，我们得到的矩阵大小一般是(4,4),具体公式如下:

• 输出矩阵:
  $$\lfloor (n_h-k_h+p_h+s_h)/s_h\rfloor \times \lfloor (n_w-k_w+p_w+s_w)/s_w\rfloor \text{\hspace{1em}(13)}$$
• 设置卷积核大小
  $$p_h=k_h-1;p_w=k_w-1\text{\hspace{1em}(14)}$$
• 输出矩阵更新为:
  $$\lfloor (n_h+s_h-1)/s_h\rfloor \times \lfloor (n_w+s_w-1)/s_w\rfloor \text{\hspace{1em}(15)}$$
• 一般能被整除，最后简化为:
  $$(n_h/s_h)\times (n_w/s_w)\text{\hspace{1em}(16)}$$

4. 多输入和多输出通道

4.1 多通道

以前我们常常进行的是矩阵运算，其有长宽两个参数，一般为二维通道，当我们的图片是彩色的.而颜色是由RGB三种颜色组成的.所以每个RGB输入图像具有 $3\times h\times w$,那么这个3就是通道的意思。

4.2 多输入通道 -> 单输出通道

假设我们输入为 $c_i\times n_h\times n_w$;卷积核为$c_i\times k_h\times k_w$,输出为$o_h\times o_w$;为了保证单通道输出，我们可以将每个通道卷积计算出来的结果求和。具体如下

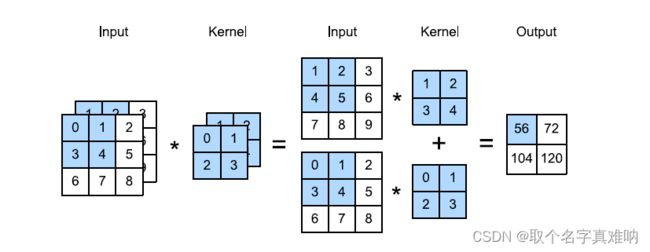
解析：

• input 输入大小为：2 x 3 x 3
• kernel 核大小为： 2 x 2 x 2
• padding 为：0；
• output 输出大小为： 1 x 2 x 2注： 3-2+1=2; 1 表示的是求和；

5. 汇聚层

6. 卷积神经网络 LeNet

注：本文代码来自 李沐的书籍，这里只做学习笔记。