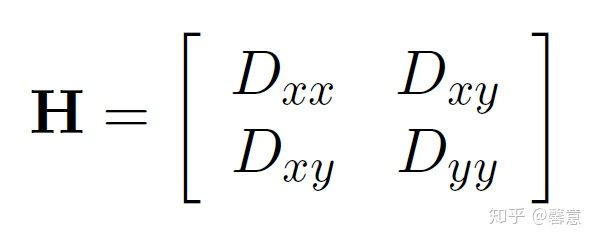python高斯噪声怎么去除_SIFT图像匹配及其python实现

1 SIFT算法基本原理

SITF算法，即尺度不变特征变换(Scale-invariant feature transform)算法，是由David G.Lowe于1999年提出，并在2004年加以完善。论文下载地址：

https://www.cs.ubc.ca/~lowe/keypoints/​www.cs.ubc.ca

Lowe将尺度的概念引入到SIFT算法中，利用SIFT方法检测图像特征点的实质就是在不同尺度空间上查找特征点，这些特征点对应的就是不同尺寸的地物。SIFT配准方法主要分为以下几个步骤：

• DOG尺度空间的建立
• 尺度空间中提取关键点
• 生成特征描述子
• 特征点匹配
• 之后便可以进行后续的配准流程，如转换模型求解、重采样等。

1.1 DOG尺度空间的构建

图像在计算机中是以二维矩阵的方式存储的，分析图像就需要提取出图像的特征，这些特征应该是具有局部不变性的显著特征，如尺度不变和旋转不变。举个例子，当人们看一个物体时，它在距离人们10米的地方和距离人们100米的地方看到的大小是不一样，这样在视网膜上成像的图像尺度其实就发生了变化。尺度不变性就是不论是在10米还是100米处成像，都能够对图像进行清晰的辨认。图像尺度空间指的就是所有尺度的图像。SIFT算法中首先进行尺度空间的构建，提取不同尺度下的关键点，这样就可以具有尺度不变性。SIFT算法中定义图像自身和尺度空间分别为

和

，则尺度空间计算公式如下：

其中

指的是在

方向和

方向上进行卷积操作，

表示尺度空间坐标。高斯核是唯一产生多尺度空间的核。使用高斯模糊对图像进行高斯平滑且降低图像细节，对图像进行2*2降采样处理，即图像长宽都降低为原来的一半，如此实现图像尺度的降低。

为了检测稳定特征点的位置，SIFT算法用DOG尺度空间来代替尺度空间函数

。通过对两幅相邻高斯尺度空间图像相减，得到DOG尺度空间。用

函数来表示DOG空间，则该尺度空间的计算公式如下：

通过上式也可以看出 DOG 尺度空间中的图像可以反映图像像素的变化，有变化的地方才有特征的存在，因此利用DOG尺度空间来定位特征点。

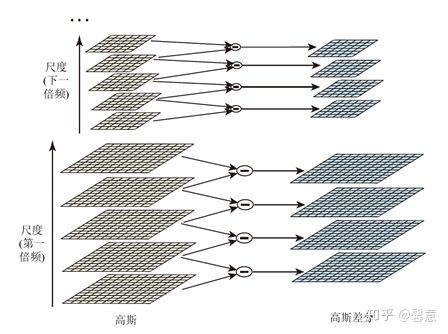
DOG 金字塔构建如图1所示。

图1 DOG金字塔构建图

1.2 DOG尺度空间中提取特征点

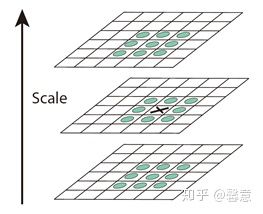
尺度空间中的所有检测点都与其同尺度相邻的8个点和上下尺度各相邻的9个点进行比较，只保留局部极值点。之后去除其中不好的关键点，通过子像元插值和剔除对比度低的点以及不稳定的边缘响应点来对精化检测到的关键点。图2是极值点检测图。

图2 极值点检测

对特征点进行子像元插值，是因为特征点的寻找是在离散空间中进行，找的特征点也是离散的，但是对于连续空间来说，离散的极值点不一定就是函数的最终极值点，所以需要用插值来找到真正的极值点。

寻找到的极值点并不是图像特征点的另一种情况是，极值点过小。图3就是有效极值点和无效极值点的示意图。如果极值点与周围像素点差距过小的话，则该极值点是无效极值点。在图像某区域中，有这样一组数据，像素点的灰度值大小依次为23、25、24，则根据上述内容，会把25当做极值点，但是从视觉上，只单纯看图像来说，这组数据代表的图像区域应该是平滑的，并且25这个点与周围点的差别不是很大，很容易受到噪声的影响，所以对这类点的剔除方法是设定阈值，若检测到的极值点没有超过阈值，则把该极值点去除掉。

图3 有效极值点和无效极值点

边缘响应较强的点就是横跨边缘处有较大的主曲率且垂直边缘处有较小主曲率的点，首先边缘上的点容易出现二义性，不能确定到底属于哪一个区域，其次易受噪声影响而变得不稳定，所以边缘响应的点一定要去除掉。

主曲率可以用Hessian矩阵H表示：

H的特征值与主曲率成正比，主曲率的变化公式如下：设

和

是H的特征值，

，其中

。则

通过计算特征值的比率来表示主曲率的变化。如果要去除边缘响应点的话，就需要垂直和横跨边缘方向上差别不是很大的点，如果差别很大的话，则说明是边缘响应点。因此要求 小于一定值。因为

为1时，

最小，当

增加时，

也会增大，所以只要控制

小于阈值，这样

会小于一定阈值，

也会小于一定的阈值，那么两个方向上的主曲率差别不大，就去除了边缘响应点。

因此，可以将满足以下公式的特征点保留，否则剔除掉。

1.3 生成特征点描述子

特征描述子包含了该描述子所在的尺度、描述子的位置以及描述子的方向。因此生成特征点描述子需要求出描述子的这三个值。尺度是已知的，因此本节主要说明如何求关键点的位置和方向信息。因为关键点还要满足尺度不变性以及一定的光照和视角不变性等，因此在描述关键点描述子的时候，要综合考虑关键点及其周围像素点的信息，这里的像素点应当是会影响关键点信息的像素点，即对关键点描述子生成有贡献的点。

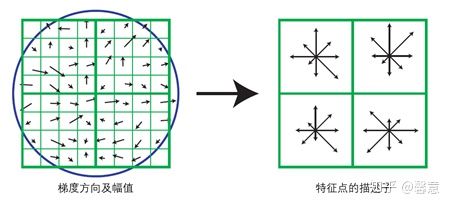
首先计算的就是关键点和它周围像素点的梯度大小和方向；计算关键点的主方向会用到梯度直方图，直方图会统计出各个方向上的像素点的个数，像素点个数最多的那个方向就是关键点的主方向。之后将坐标轴方向和关键点主方向保持一致，便能够满足旋转不变性。

准备工作完成后，计算关键点描述子，因为描述关键点不仅与其自身有关，还与它周围的像素点有关，所以将以该特征点为中心的邻域划分成4×4的区域，即特征点周围形成了16个小区域。然后利用梯度直方图统计每个小区域内各方向像素点的个数，那么此区域中与关键点有关的信息就是各个方向的像素点数。因为共有8个方向，且每个方向的像素点数就是一种信息，因此每个区域内会出现8种信息，关键点周围一共形成了16个区域，每个区域8种信息，一共128种信息，而这些信息都要记录在关键点描述子中，所以描述子一共128维。图4是SIFT特征描述子生成图。

图4 SIFT特征描述子生成

1.4 特征点匹配

使用欧氏距离来判断两幅图像特征点的相似性。在匹配过程中，SIFT算法使用的是Kd-tree算法，即找出待配准图像中与参考图像特征点A距离最近的点B和距离次近的点C，则判断特征点A与B是一对匹配点的公式为：

其中d(A,B)为A和距离A最近的点B之间的距离，d(A,C)为A和距离A次近的点C之间的距离。

之后用RANSAC算法消除错误匹配点，至此SIFT特征点提取和匹配工作已经完成。RANSAC是一种随机参数估计算法，它的具体步骤为:

1. 从初始匹配点对集中随机选取8个匹配点对作为样本初始化模型，确定一个模型的参数；
2. 用此模型检测初始匹配点对集，找到满足该模型阈值的所有内点(符合模型的数据)；
3. 统计由该模型得到的内点数量；
4. 重复步骤1-3，当得到的内点数量最多、误差最小时停止；
5. 输出最多的内点集，该内点集即为经过RANSAC筛选后的匹配点对集。

2 代码实现

代码采用python语言编写，设计到的第三方库包括matplotlib、OpenCV、numpy等。OpenCV可能会遇到无法调用Sift模块问题，请参照：

故梦：python使用Opencv的Sift/Surf算法​zhuanlan.zhihu.com

2.1 加载并显示图像

import matplotlib.image as mpimg
import matplotlib.pyplot as plt

image1 = mpimg.imread("01.jpg")
image2 = mpimg.imread("02.jpg")

plt.figure()
plt.imshow(image1)
plt.savefig('image1.png', dpi = 300)

plt.figure()
plt.imshow(image2)
plt.savefig('image2.png', dpi = 300)

输出：

image1.png

image2.png

2.2 特征点提取&生成描述

import cv2
import time

#  计算特征点提取&生成描述时间
start = time.time()
sift = cv2.xfeatures2d.SIFT_create()
#  使用SIFT查找关键点key points和描述符descriptors
kp1, des1 = sift.detectAndCompute(image1, None)
kp2, des2 = sift.detectAndCompute(image2, None)
end = time.time()
print("特征点提取&生成描述运行时间:%.2f秒"%(end-start))

kp_image1 = cv2.drawKeypoints(image1, kp1, None)
kp_image2 = cv2.drawKeypoints(image2, kp2, None)

plt.figure()
plt.imshow(kp_image1)
plt.savefig('kp_image1.png', dpi = 300)

plt.figure()
plt.imshow(kp_image2)
plt.savefig('kp_image2.png', dpi = 300)

输出：

特征点提取&生成描述运行时间:2.60秒

kp_image1.png

kp_image2.png

#  查看关键点
print("关键点数目:", len(kp1))

for i in range(2):
    print("关键点", i)
    print("数据类型:", type(kp1[i]))
    print("关键点坐标:", kp1[i].pt)
    print("邻域直径:", kp1[i].size)
    print("方向:", kp1[i].angle)
    print("所在的图像金字塔的组:", kp1[i].octave)
    print("================")

#  查看描述
print("描述的shape:", des1.shape)
for i in range(2):
    print("描述", i)
    print(des1[i])

输出：

关键点数目: 19158
关键点 0
数据类型: 
关键点坐标: (3.075269937515259, 1546.7645263671875)
邻域直径: 2.406801223754883
方向: 77.8153076171875
所在的图像金字塔的组: 4457215
================
关键点 1
数据类型: 
关键点坐标: (3.701429605484009, 1531.2259521484375)
邻域直径: 2.497684955596924
方向: 212.90887451171875
所在的图像金字塔的组: 7144191
================
描述的shape: (19158, 128)
描述 0
[  1.   0.   1.   1.   0.   7.  12.   7.  49.   1.   1.   0.   0.   0.
   8.  68.  28.   0.   0.   0.   1.  76. 106.  69.  16.   9.   0.   0.
   0.  79.  46.   2.   0.   0.   0.   0.   2.  83.  82.   6. 151.   4.
   0.   0.   0.   6.  58.  75. 151.  29.   0.   0.   0.  93. 124. 109.
  15.   3.   0.   0.   0. 151. 134.   8.   0.   0.   0.   0.   7.  53.
  50.   0.  54.   2.   0.   0.   0.   9.  87.  50. 151.  41.   0.   0.
   0.   8.  12.  54.  79.   8.   0.   0.   4. 151.  29.  14.   0.   0.
   0.   0.   0.   0.   0.   0.   2.   0.   0.   0.   0.   0.   1.   2.
  31.   0.   0.   0.   0.   0.   0.   7.  15.   0.   0.   0.   2.  17.
   1.   5.]
描述 1
[ 76.  38.   0.   0.   0.   0.   0.   0. 151.  66.   1.   1.   1.   0.
   0.   5.  31.   8.   1.   8.   3.   0.   0.   1.   0.   0.   0.   0.
   0.   0.   0.   0.  86.  14.   0.   0.   1.   2.   1.   4. 151.  41.
   9.  18.  13.   0.   0.  22.  43.   8.   9. 137. 101.   0.   0.   5.
   0.   0.   0.  15.   7.   0.   0.   0.  59.  13.   3.   1.   0.   2.
   3.   8. 151.  98. 116.  51.   3.   0.   0.   7.  14.  11.  88. 151.
  43.   1.   9.  77.   1.   0.   0.  18.   8.   0.  24. 120.   9.   8.
   5.   3.   0.   0.   8.   4.  24.  14.  38.  21.   1.   0.   0.  51.
  59.   2.  18.  11.   1.   0.   9. 151.   5.   0.   2.  21.  12.   2.
  27. 151.]

2.3 画出对应匹配

ratio = 0.85

#  计算匹配点匹配时间
start = time.time()

#  K近邻算法求取在空间中距离最近的K个数据点，并将这些数据点归为一类
matcher = cv2.BFMatcher()
raw_matches = matcher.knnMatch(des1, des2, k = 2)
good_matches = []
for m1, m2 in raw_matches:
    #  如果最接近和次接近的比值大于一个既定的值，那么我们保留这个最接近的值，认为它和其匹配的点为good_match
    if m1.distance < ratio * m2.distance:
        good_matches.append([m1])
end = time.time()
print("匹配点匹配运行时间:%.2f秒"%(end-start))

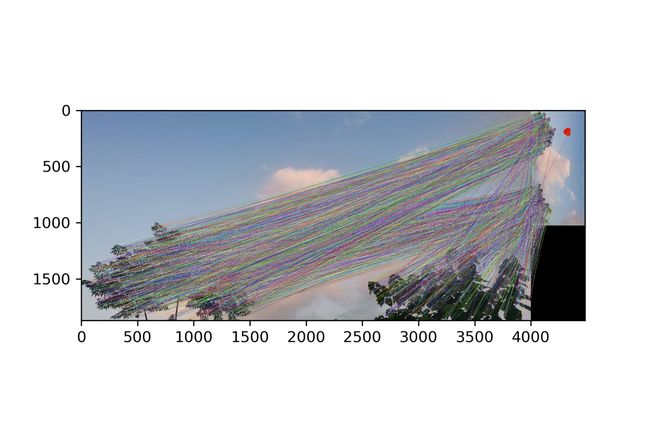
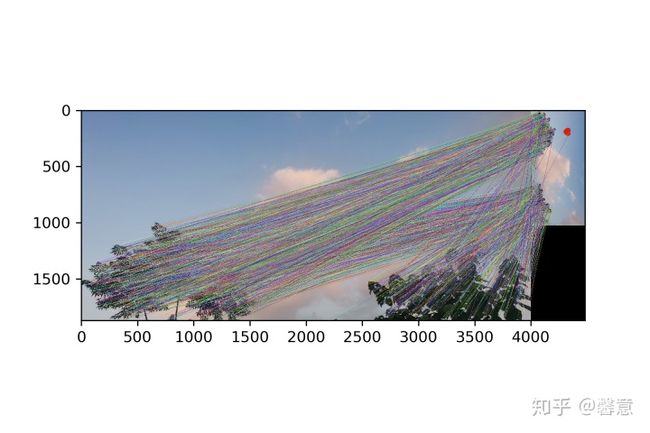
matches = cv2.drawMatchesKnn(image1, kp1, image2, kp2, good_matches, None, flags = 2)

plt.figure()
plt.imshow(matches)
plt.savefig('matches.png', dpi = 300)

输出：

匹配点匹配运行时间:0.74秒

matches.png

#  匹配对的数目
print("匹配对的数目:", len(good_matches))
for i in range(2):
    print("匹配", i)
    print("数据类型:", type(good_matches[i][0]))
    print("描述符之间的距离:", good_matches[i][0].distance)
    print("查询图像中描述符的索引:", good_matches[i][0].queryIdx)
    print("目标图像中描述符的索引:", good_matches[i][0].trainIdx)
    print("================")

输出：

匹配对的数目: 2594
匹配 0
数据类型: 
描述符之间的距离: 248.94175720214844
查询图像中描述符的索引: 6
目标图像中描述符的索引: 627
================
匹配 1
数据类型: 
描述符之间的距离: 43.931766510009766
查询图像中描述符的索引: 18
目标图像中描述符的索引: 815
================

2.4 图像匹配

import numpy as np

#  单应性矩阵有八个参数，每一个对应的像素点可以产生2个方程(x一个，y一个)，那么需要四个像素点就能解出单应性矩阵
if len(good_matches) > 4:
    #  计算匹配时间
    start = time.time()
    ptsA= np.float32([kp1[m[0].queryIdx].pt for m in good_matches]).reshape(-1, 1, 2)
    ptsB = np.float32([kp2[m[0].trainIdx].pt for m in good_matches]).reshape(-1, 1, 2)
    ransacReprojThreshold = 4
    #  单应性矩阵可以将一张图通过旋转、变换等方式与另一张图对齐
    H, status =cv2.findHomography(ptsA,ptsB,cv2.RANSAC,ransacReprojThreshold);
    imgOut = cv2.warpPerspective(image2, H, (image1.shape[1],image1.shape[0]),flags=cv2.INTER_LINEAR + cv2.WARP_INVERSE_MAP)
    end = time.time()
    print("匹配运行时间:%.2f秒"%(end-start))
    
    plt.figure()
    plt.imshow(image1)
    plt.figure()
    plt.imshow(image2)
    plt.figure()
    plt.imshow(imgOut)
    plt.savefig('imgOut.png', dpi = 300)

输出：

匹配运行时间:0.06秒

imgOut.png

参考文献

1. Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110.
2. 祁曦. 基于改进SIFT和改进K-means的遥感图像配准算法[D].华东师范大学,2018.