Distilling Holistic Knowledge with Graph Neural Networks论文解读

这是一篇ICCV2021的文章，提出了一种新的知识蒸馏方式(Holistic Knowledge Distillation)
原文链接
代码链接
Figure 1为Individual、Relational、Holistic Knowledge Distillation三种不同的知识蒸馏方式的区别.这里根据Relational Knowledge Distillation解读以及Relational Knowledge Distillation简单介绍一下这几种知识蒸馏方式的区别：


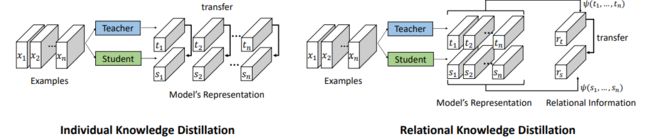
先根据Relational Knowledge Distillation论文中的图来解释传统的知识蒸馏以及Relational Knowledge Distillation。由上图可以看出传统KD是对单张图片分别根据学生和老师模型提取特征向量，并通过KL散度以及其他方法来计算学生和老师模型输出的差异，所以这里point to point就很好理解了。Relational Knowledge Distillation在传统KD的基础上，将多张图片的特征向量通过distance-wise (second-order) and angle-wise (third-order) distillation losses合在一起进行学习。

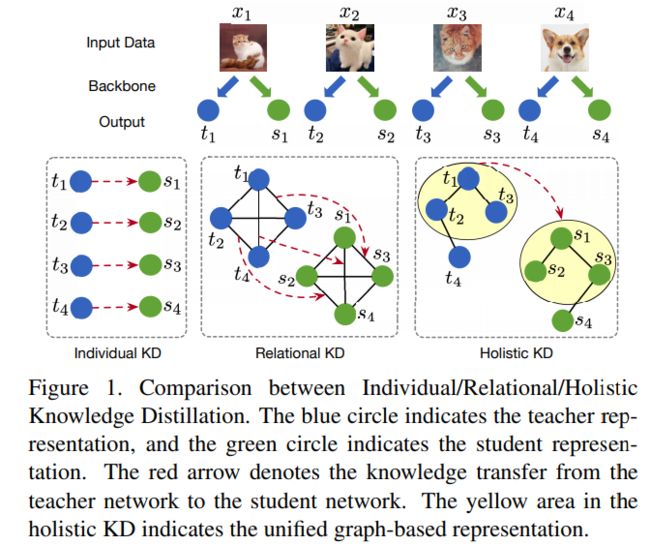
而本文认为单一的提取个体的信息和单一的提取个体间的信息是不够的，因此提出了Holistic Knowledge Distillation，整合了传统KD和Relational Knowledge Distillation。

先验知识

给定一个从K类数据集中采样得到的$X=\{x_1,x_2,...x_N\}$，带有相应的标签$Y=\{y_1,y_2,...y_N\}$，其中N表示采样的个数。$W^t$和$W^s$分别表示固定参数的优化好的教师模型和可训练参数的学生模型，老师模型和学生模型的特征表示(经常用于Relational Knowledge Distillation)分别为$f^t\in R^{d^t}$和$f^s\in R^{d^s}$，其中$d^t$和$d^s$在模型结构不同时可能不同，$z^t$和$z^s$分别是老师和学生模型的logits预测。
$$p_i(z;r)=Softmax(z;r)=\frac{e^{\frac{z_i}{r}}}{{\sum }_{k=1}^K{e}^{\frac{z_k}{r}}}$$
上式初始温度$r=1$,随着$r$的逐渐增大,softmax的output probability distribution越趋于平滑，其分布的熵越大，负标签携带的信息会被相对地放大，模型训练将更加关注负标签。
$$L_{KD}(p^s,p^t)=\frac{1}{N}\sum _{i=1}^{N}KL(p^s,p^t)$$
上式为老师模型的软标签概率和学生模型的概率分布求KL散度。
在vanilla KD中，学生模型的损失表示为：
$$L=L_{CE}(p^s,y)+\lambda L_{KD}(p^s,p^t)$$

Attributed Context Graph Construction

输入batch组图片到老师和学生模型得到特征表示$f^t$，$f^s$以及预测概率$p^t$，$p^s$。接着构建两个属性图$G^t=\{A^t,F^t\}$和$G^s=\{A^s,F^s\}$, 其中$F^t\in R^{N\times d^t}$,$F^s\in R^{N\times d^s}$是图中节点的属性。$A^t,A^s$基于$p^t,p^s$得到的
$$A^t=\varphi (p^t),A^s=\varphi (p^s)$$
其中$\varphi (.)$是基于KNN的图重构函数(不是很懂这个图是怎么构建出来的)。$G^t$是fixed，相比于全连接的graph，KNN的graph可以滤除不相关的样本对。插播KNN学习（关于KNN的学习基本按照一文搞懂k近邻（k-NN）算法（一）和Python—KNN分类算法（详解）来讲解的）
KNN又叫K Nearest Neighbors，即通过与待预测节点的K个最近节点来预测当前节点。如图所示：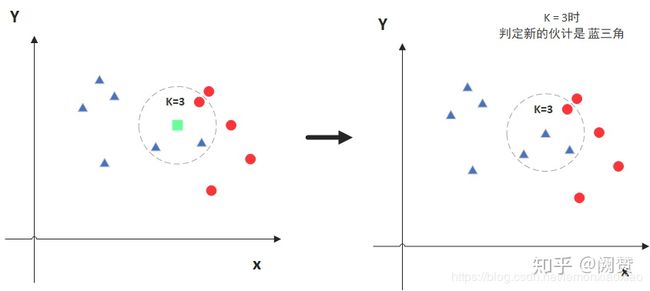
对于KNN而言，K的选取很重要。因为K取小了会导致过拟合：

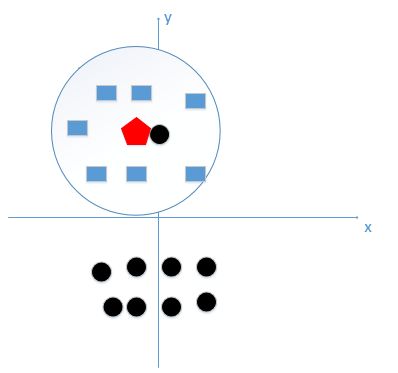
因为对于上图来说正确的方式应该是蓝色的圈内的节点数做K值，而如果K值过小，极端情况为1时，待预测的红色节点最近的节点是黑色，而这显然不正确，它学到的完全是个噪声。

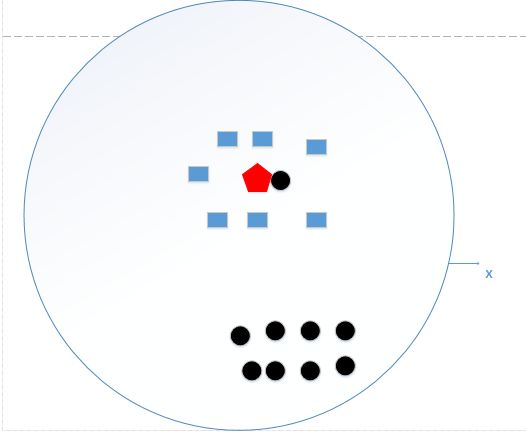
相反当K值过大时，如上图所示，其预测值是在全局的范围内寻找点数量最多的那个即可，上述过程中待预测的节点应该是黑色，因为黑色点比蓝色方块多，然而显然是有问题的。下图才是真正正确的K值选取范围：

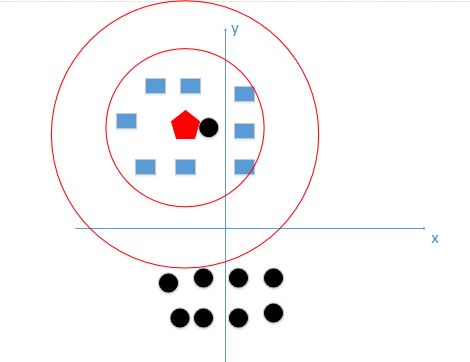
说完K值对KNN的影响，再来看看距离度量的选取（毕竟有那么多种度量方式），一般KNN都选择欧式距离作为度量的方式。
最后需要对所给特征进行归一化，因为特征不同，不归一化会导致预测时会有特征偏好，具体例子详见一文搞懂k近邻（k-NN）算法（一）。
附上论文knn_graph部分源代码和dgl官网代码Source code for dgl.transform：

def cos_distance_softmax(x):
    soft = F.softmax(x, dim=2)
    w = soft.norm(p=2, dim=2, keepdim=True)
    # L2范数
    print(B.swapaxes(soft, -1, -2))  # 将soft转置
    return 1 - soft @ B.swapaxes(soft, -1, -2) / (w @ B.swapaxes(w, -1, -2)).clamp(min=eps)  # soft * soft^{T}


def knn_graph(x, k):
    if B.ndim(x) == 2:
        x = B.unsqueeze(x, 0)
    n_samples, n_points, _ = B.shape(x)

    dist = cos_distance_softmax(x)  # 这里不太清楚为什么要用这个distance

    fil = 1 - torch.eye(n_points, n_points)
    dist = dist * B.unsqueeze(fil, 0).cuda()
    dist = dist - B.unsqueeze(torch.eye(n_points, n_points), 0).cuda()

    k_indices = B.argtopk(dist, k, 2, descending=False)

    dst = B.copy_to(k_indices, B.cpu())
    src = B.zeros_like(dst) + B.reshape(B.arange(0, n_points), (1, -1, 1))

    per_sample_offset = B.reshape(B.arange(0, n_samples) * n_points, (-1, 1, 1))
    dst += per_sample_offset
    src += per_sample_offset
    dst = B.reshape(dst, (-1,))
    src = B.reshape(src, (-1,))
    adj = sparse.csr_matrix((B.asnumpy(B.zeros_like(dst) + 1), (B.asnumpy(dst), B.asnumpy(src))))

    g = DGLGraph(adj, readonly=True)
    return g

Holistic Knowledge Distillation

用Topology Adaptive Graph Convolution Network (TAGCN)提取$G^t$,$G^s$的holistic knowledge，用$H^t\in R^{N\times g^t}$和$H^s\in R^{N\times g^s}$
$$H^t=\sum _{l=0}^L(D_t^{-1/2}{A}^t{D}_t^{-1/2}{)}^l{F}^t{\theta }_l^t$$$$H^s=\sum _{l=0}^L(D_s^{-1/2}{A}^s{D}_s^{-1/2}{)}^l{F}^s{\theta }_l^s$$
其中$g^t$,$g^s$是图表示的维度，$D_t={\sum }_j{A}_{ij}^t$是教师模型的对角线度矩阵，${\theta }_l^t$,${\theta }_l^s$是可学习的权重。
使用互信息来蒸馏学生模型，使其最大化$H^t$和$H^s$之间的互信息。
$$\underset{W^s,{\theta }^t,{\theta }^s}{L_{HOL}}=-I(H^t,H^s)$$其中$I(H^t,H^s)$用InfoNCE estimator来计算
$$I(H^t,H^s)\ge E[\frac{1}{N}\sum _{i=1}^{N}log\frac{e^{f(h_i^t,h_i^s)}}{\frac{1}{N}{\sum }_{j=1}^N{e}^{f(h_i^t,h_i^s)}}]$$$f(.)$是余弦相似性，$h_i^t$，$h_i^s$是实例i由老师模型和学生模型分别学到的表示。
最终holistic知识蒸馏的目标函数是$$L=L_{CE}+\beta L_{HOL}$$

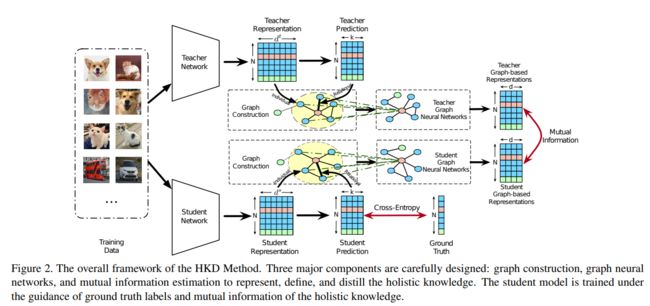
插播TAGCN相关知识（根据参考文献系列教程GNN-algorithms之六：《多核卷积拓扑图—TAGCN》）：
好吧，不想重复劳动了，直接从参考文献里截图了。简单来说就是把不同阶邻域的特征进行加权聚合。

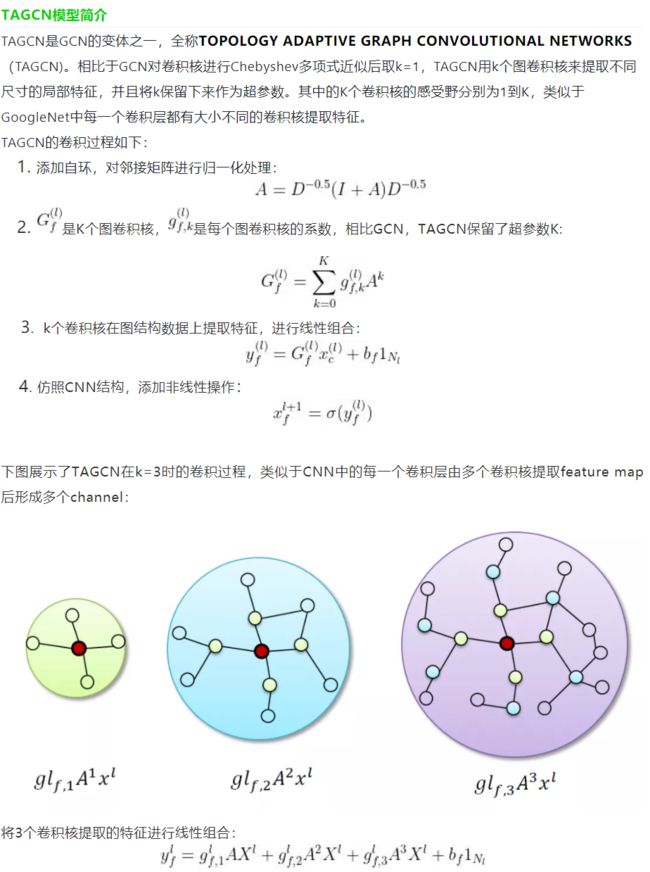
TAGCN卷积的dgl官方源码：

"""Torch Module for Topology Adaptive Graph Convolutional layer"""
import torch as th
from torch import nn

from .... import function as fn


class TAGConv(nn.Module):
    def __init__(self,
                 in_feats,
                 out_feats,
                 k=2,
                 bias=True,
                 activation=None,
                 ):
        super(TAGConv, self).__init__()
        self._in_feats = in_feats
        self._out_feats = out_feats
        self._k = k
        self._activation = activation
        self.lin = nn.Linear(in_feats * (self._k + 1), out_feats, bias=bias)

        self.reset_parameters()

    def reset_parameters(self):
        gain = nn.init.calculate_gain('relu')
        nn.init.xavier_normal_(self.lin.weight, gain=gain)

    def forward(self, graph, feat):
        with graph.local_scope():
            assert graph.is_homogeneous, 'Graph is not homogeneous'

            norm = th.pow(graph.in_degrees().float().clamp(min=1), -0.5)
            shp = norm.shape + (1,) * (feat.dim() - 1)
            norm = th.reshape(norm, shp).to(feat.device)  # 貌似就做了个转置？

            #D-1/2 A D -1/2 X
            fstack = [feat]  # 后面说实话没怎么懂
            for _ in range(self._k):

                rst = fstack[-1] * norm
                graph.ndata['h'] = rst

                graph.update_all(fn.copy_src(src='h', out='m'),
                                 fn.sum(msg='m', out='h'))
                rst = graph.ndata['h']  # 单个节点的特征
                rst = rst * norm
                fstack.append(rst)

            rst = self.lin(th.cat(fstack, dim=-1))

            if self._activation is not None:
                rst = self._activation(rst)

            return rst

文章所用模型结构VGG19_BN:

Efficient Training

由于InfoNCE estimator需要对数据集中每个样本作为负样本计算，对于大数据集成本太高，因此文章使用Memory Bank strategy来储存。由于文章对mini-batch的样本进行随机采样（吧啦吧啦看不懂。。。不敢乱翻译，贴原文，如果有人看懂了请评论区踢我一脚）


接着就有了下面的改进版公式：
$$L_{HOL}=\sum _{i=1}^{N}log\frac{e^{f(h_i^t,h_i^s)}}{e^{f(h_i^t,h_i^s)}+{\sum }_{j=1,j\ne i}^N{e}^{f(h_i^t,f_j^s)}}+log\frac{e^{f(h_i^s,h_i^t)}}{e^{f(h_i^s,h_i^t)}+{\sum }_{j=1,j\ne i}^N{e}^{f(h_i^s,f_j^t)}}$$
总体伪代码。这个还是很好懂的：

接着文章还写了现有的KD方法的介绍以及对比，这里不再详述，只看方法的机器。

实验

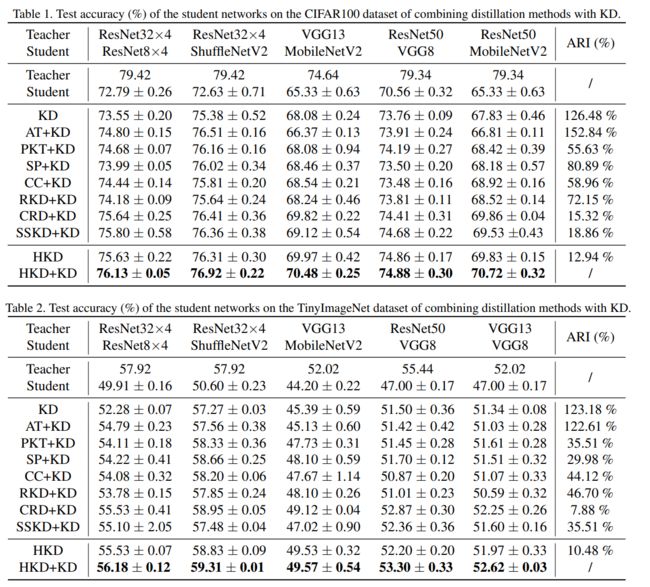
没怎么看，这里就随便放了一个比较的图，还有其他的一些分析详见原文。

参考文献

深度学习中的互信息：无监督提取特征
Relational Knowledge Distillation解读
Relational Knowledge Distillation
一文搞懂k近邻（k-NN）算法（一）
Python—KNN分类算法（详解）
系列教程GNN-algorithms之六：《多核卷积拓扑图—TAGCN》
Source code for dgl.transform