样本
正样本:即属于某一类(一般是所求的那一类)的样本。在本例中是及格的学生。
负样本:即不属于这一类的样本。在本例中是不及格的学生。
y_pred = [0, 0, 0, 0, 0, 0, 1, 1, 1, 1]
y_true = [0, 0, 0, 0, 1, 1, 1, 1, 0, 0]
上述 0 代表不及格,1 代表及格。这里正样本代表及格。
TP、FP、FN、TN
| 正类 | 负类 | |
|---|---|---|
| 被检索 | True Positive | False Positive |
| 未检索 | False Negative | True Negative |
- TP:被检索到正样本,实际也是正样本(正确识别)
在本例表现为:预测及格,实际也及格。本例 TP=2
- FP:被检索到正样本,实际是负样本(一类错误识别)
在本例表现为:预测及格,实际不及格。本例 FP=2
- FN:未被检索到正样本,实际是正样本。(二类错误识别)
在本例表现为:预测不及格,实际及格了。本例 FN=2
- TN:未被检索到正样本,实际也是负样本。(正确识别)
在本例表现为:预测不及格,实际也不及格。本例 TN=4
from sklearn.metrics import confusion_matrix
y_true = [0, 0, 0, 0, 1, 1, 1, 1, 0, 0]
y_pred = [0, 0, 0, 0, 0, 0, 1, 1, 1, 1]
TN, FP, FN, TP = confusion_matrix(y_true, y_pred).ravel()
print(TN, FP, FN, TP)
结果:4 2 2 2
Accuracy(准确率、精度)
$\operatorname{acc}(f ; D) =\frac{1}{m} \sum \limits _{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right)=y_{i}\right) =1-E(f ; D)$$A C C=\frac{T P+T N}{T P+T N+F P+F N}$
y_pred = [0, 0, 0, 0, 0, 0, 1, 1, 1, 1]
y_true = [0, 0, 0, 0, 1, 1, 1, 1, 0, 0]
from sklearn.metrics import accuracy_score
y_true = [0, 0, 0, 0, 1, 1, 1, 1, 0, 0]
y_pred = [0, 0, 0, 0, 0, 0, 1, 1, 1, 1]
print(accuracy_score(y_true, y_pred))
结果:
0.6
Precision(精确率、查准率)
$P=\frac{T P}{T P+F P}$y_pred = [0, 0, 0, 0, 0, 0, 1, 1, 1, 1]
y_true = [0, 0, 0, 0, 1, 1, 1, 1, 0, 0]
-
- 不及格类:检索到 6人,正确检索 4人,所以Precision = 4 / 6 = 0.6667.
- 及格类:检索到 4 人,正确检索 2人,所以Precision = 2 / 4 = 0.5.
代码:
from sklearn.metrics import precision_score
y_true = [0, 0, 0, 0, 1, 1, 1, 1, 0, 0]
y_pred = [0, 0, 0, 0, 0, 0, 1, 1, 1, 1]
print(precision_score(y_true, y_pred, average=None)) #4/6 2/4
结果:
[0.66666667 0.5 ]
Recall (召回率、查全率)
$P=\frac{T P}{T P+F P}$
被正确检索 (y_pred) 的样本数 与 应当被检索 (y_true) 到的样本数之比。(这里暂时先不适应上述相同样本数据,否则和Precision结果一样,怕搞混)
y_true = [0, 0, 0, 0, 1, 1, 1, 1, 0, 0]
y_pred = [0, 0, 0, 1, 1, 1, 1, 0, 1, 1]
在本例中,
-
- 不及格类:应当检索到 6人,正确检索 3人,所以 Recall = 3 / 6 = 0.5.
- 及格类:应当检索到 4 人,正确检索 3人,所以 Recall = 3 / 4 = 0.75.
结果:
[0.5 0.75]
F1 Score
$F 1=\frac{2 \times P \times R}{P+R}$
在本例中,
y_true = [0, 0, 0, 0, 1, 1, 1, 1, 0, 0]
y_pred = [0, 0, 0, 1, 1, 1, 1, 0, 1, 1]
-
- 不及格类:P=3/4, R=3/6
- 及格类:P=3/6, R=3/4
代码:
from sklearn.metrics import recall_score,precision_score,f1_score
y_true = [0, 0, 0, 0, 1, 1, 1, 1, 0, 0]
y_pred = [0, 0, 0, 1, 1, 1, 1, 0, 1, 1]
print(precision_score(y_true, y_pred, average=None))
print(recall_score(y_true, y_pred, average=None))
print( f1_score(y_true, y_pred, average=None ))
# 不及格类
p=3/4
r=3/6
print((2*p*r)/(p+r))
# 及格类
p=3/6
r=3/4
print((2*p*r)/(p+r))
结果:
[0.75 0.5 ]
[0.5 0.75]
[0.6 0.6]
0.6
0.6
宏平均
是先对每一个类统计指标值,然后在对所有类求算术平均值。
$macro-P =\frac{1}{n} \sum \limits _{i=1}^{n} P_{i}$
$macro -R =\frac{1}{n} \sum \limits _{i=1}^{n} R_{i}$
$macro -F1 =\frac{2 \times macro-P \times macro-R}{macro-P+macro-R}$
代码:
from sklearn.metrics import recall_score,precision_score,f1_score
y_true = [0, 0, 0, 0, 1, 1, 1, 1, 0, 0]
y_pred = [0, 0, 0, 1, 1, 1, 1, 0, 1, 1]
print(precision_score(y_true, y_pred, average=None))
print(recall_score(y_true, y_pred, average=None))
print(precision_score(y_true, y_pred, average="macro"))
print(recall_score(y_true, y_pred, average="macro"))
print(f1_score(y_true, y_pred, average="macro"))
结果:
[0.75 0.5 ]
[0.5 0.75]
0.625
0.625
0.6
微平均
是对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵,然后计算相应指标。
$micro-P=\frac{\overline{T P}}{\overline{T P}+\overline{F P}} $
$micro-R=\frac{\overline{T P}}{\overline{T P}+\overline{F N}} $
$micro-F 1=\frac{2 \times micro-P \times micro-R}{ micro-P+\text { micro }-R}$
看成一类,造成的结果是 $micro-P = micro-R $。
代码:
from sklearn.metrics import recall_score,precision_score,f1_score
y_true = [0, 2, 2, 0, 1, 1, 1, 1, 0, 0]
y_pred = [0, 0, 2, 1, 1, 1, 1, 0, 1, 1]
print(precision_score(y_true, y_pred, average="micro"))
print(recall_score(y_true, y_pred, average="micro"))
print(f1_score(y_true, y_pred, average="micro"))
结果:
0.5
0.5
0.5
混淆矩阵
第 $i$ 行代表第 $i$-th class,每列表示把 $i$-th class 分配到 $j$-th class 中的个数
代码:
from sklearn.metrics import confusion_matrix
y_true = [1, 1, 1, 2, 2, 3]
y_pred = [1, 1, 2, 1, 2, 3]
print(confusion_matrix(y_true, y_pred))
结果:
[[2 1 0]
[1 1 0]
[0 0 1]]
代码:
y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
print(confusion_matrix(y_true, y_pred, labels=["ant", "bird", "cat"]))
结果:
[[2 0 0]
[0 0 1]
[1 0 2]]
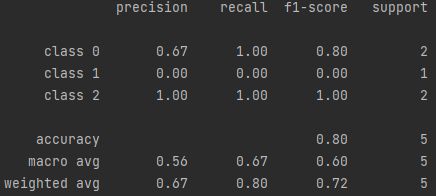
分类报告
将上述结果,用report的形式展示出来
代码:
from sklearn.metrics import classification_report
y_true = [0, 1, 2, 2, 0]
y_pred = [0, 0, 2, 2, 0]
target_names = ['class 0', 'class 1', 'class 2']
print(classification_report(y_true, y_pred, target_names=target_names))
结果:
真正率、假正率
真正率 (TPR ) = 灵敏度/召回率 = TP/(TP+FN)TP/(TP+FN) 正例中有多少样本被检测出
假正率 (FPR ) = 1- 特异度 = FP/(FP+TN)FP/(FP+TN) 负例中有多少样本被错误覆盖
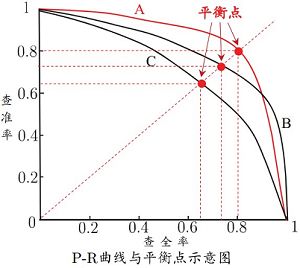
P-R曲线
- 若一个学习算法的PR曲线被另一个学习算法的曲线完全“包住”,则可认为后者的性能优于前者,如A优于C;
- 若两个学习算法的PR曲线发生交叉(如A和B),则难以判断孰优孰劣,只能在具体的查准率和查全率条件下进行比较;
- 可通过比较P-R曲线下的面积(PR-AUC)
- 利用平衡点(即P=R时的取值)
- 利用F1度量
ROC
AUC
代价敏感错误率
略