sklearn机器学习(六)逻辑回归实例乳腺癌检测
本节采用逻辑回归算法完成乳腺癌的检测。
逻辑回归主要用于这种二项分类问题,采用sigmoid函数作为预测函数,当x=0时,sigmoid函数的值为0.5,之后向两边趋近,因此它得到的结果都是非黑及白的。例如划分乳腺癌是为阴性还是阳性,就比较好划分
from sklearn.datasets import load_breast_cancer
cancer=load_breast_cancer()#加载乳腺癌数据
x=cancer.data#加载乳腺癌判别特征
y=cancer.target#两个特征,y=0时为阴性,y=1时为阳性
print('data shape:{0};no.positive:{1};no.negative:{2}'.format(x.shape,y[y==1].shape,y[y==0].shape))
print(cancer.data[0])#输出
以下是上代码块的输出:
data shape:(569, 30);no.positive:(357,);no.negative:(212,)
[1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
4.601e-01 1.189e-01]
从中我们可以看出X中data一共有569个数据,30个特征。只是其关注特征其实为10个,即为
radius:半径,即病灶中心点离边界的平均距离
texture:纹理,灰度值的标准偏差
perimeter:周长,即病灶的大小
area:面积,反映病灶大小的一个指标
smoothness:平滑度,即半径的变化幅度
compactness:密实度,周长的平方除以面积的熵,再减一
concavity:凹度,凹陷部分轮廓的严重程度
concave points:凹点,凹陷轮廓的数量
symmetry:对称性
fractal dimension:分形维度
每一个有着对应的标准差与最大值,所以这里会有30个特征值。
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)#划分训练集和测试集
from sklearn.linear_model import LogisticRegression
model=LogisticRegression()#逻辑回归模型的建立
model=fit(X_train,y_train)#逻辑回归模型的训练
train_score=model.score(X_train,y_train)#训练的得分
test_score=model.score(X_test,y_test)#测试得分
print('train score:{train_score:.6f};test score:{test_score:.6f}'.format(train_score=train_score,test_score=test_score))
输出如下:
train score:0.960440;test score:0.938596
看起来效果还不错。
import numpy as np
y_pred=model.predict(X_test)#进行预测
print('matchs:{0}/{1}'.format(np.equal(y_pred,y_test).shape[0],y_test.shape[0]))#test集的预测对比
输出如下
matchs:114/114
预测成功率达到了惊人的100%,这是怎么回事呢?
其实我们这个模型是非黑及白的,所以它是以是阴性或者是阳性的几率,哪个超过了50%,就会判定为哪个。
所以说其实他的实际预测率并没有达到那么高,只是恰巧全部都没错。
如果我们将在阴性超过10%的样本中找阳性概率超过10%的,其预测误自信度就低了。
来看一下,下面的代码:
y_pred_proba=model.predict_proba(X_test)#计算每个样本的预测概率
print('sample of predict probability:{0}'.format(y_pred_proba[0]))#第一样本的预测概率
y_pred_proba_0=y_pred_proba[:,0]>0.1#预测阴性超过10%的样本
result=y_pred_proba[y_pred_proba_0]#对结果集再度计算预测概率
y_pred_proba_1=result[:,1]>0.1#其中阳性大于10%的
print(result[y_pred_proba_1])#输出
输出如下:
sample of predict probability:[0.99439345 0.00560655]
[[0.65750639 0.34249361]
[0.88660424 0.11339576]
[0.45493365 0.54506635]
[0.19960688 0.80039312]
[0.72325374 0.27674626]
[0.88006323 0.11993677]
[0.18469886 0.81530114]
[0.50891906 0.49108094]
[0.10968585 0.89031415]
[0.13693387 0.86306613]
[0.17339546 0.82660454]
[0.87115846 0.12884154]
[0.77827742 0.22172258]
[0.11693239 0.88306761]
[0.59116034 0.40883966]
[0.6807513 0.3192487 ]
[0.17420797 0.82579203]
[0.19818432 0.80181568]
[0.25355262 0.74644738]]
接下来就是模型的优化了。
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
def polynomial_model(degree=1,**kwarg):#**kwarg是正则项的输入
polynomial_features=PolynomialFeatures(degree=degree,include_bias=False)#多项式
logistic_regression=LogisticRegression(**kwarg)#逻辑回归模型的建立
pipeline=Pipeline([("polynomial_features",polynomial_features),("logistic_regression",logistic_regression)])#生成模型
return pipeline
使用二次多项式特征进行优化:
import time
model=polynomial_model(degree=2,penalty='l1')#使用L1范式作为正则项,进行稀疏化
start=time.clock()#计时开始
model.fit(X_train,y_train)#训练模型
train_score=model.score(X_train,y_train)#训练集分数
cv_score=model.score(X_test,y_test)#test集分数
print('elaspe:{0:.6f};train_score:{1:.6f};cv_socre:{2:.6f};'.format(time.clock()-start,train_score,cv_score))
输出如下:
elaspe:0.592511;train_score:1.000000;cv_socre:0.964912;
模型参数的稀疏化后会导致模型参数的增多,因此我们也来观察以下一共生成了多少个参数,又有多少个是有用的呢。
logistic_regression=model.named_steps['logistic_regression']
print('model parameters shape:{0};count of non-zero element:{1}'.format(
logistic_regression.coef_.shape,np.count_nonzero(logistic_regression.coef_)))
输出如下:
model parameters shape:(1, 495);count of non-zero element:86
从上我们可以看出,模型参数从30个变成495个,而实际有用的只有86个。其中的coef_是有模型的有效特征参数
剩下就是画出学习曲线,这段代码已经很熟,就不做过多解读。如果看不懂,请看本系列(一)
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
import numpy as np
import matplotlib.pyplot as plt
def plot_learning_curve(estimator,title,X,y,ylim=None,cv=None,n_jobs=1,train_sizes=np.linspace(0.1,1.0,5)):
plt.title(title)#图像标题
if ylim is not None:#y轴限制不为空时
plt.ylim(*ylim)
plt.xlabel("Training examples")#两个标题
plt.ylabel("Score")
train_sizes,train_scores,test_scores=learning_curve(estimator,X,y,cv=cv,n_jobs=n_jobs,train_sizes=train_sizes)#获取训练集大小,训练得分集合,测试得分集合
train_scores_mean=np.mean(train_scores,axis=1)#将训练得分集合按行的到平均值
train_scores_std=np.std(train_scores,axis=1)#计算训练矩阵的标准方差
test_scores_mean=np.mean(test_scores,axis=1)
test_scores_std=np.std(test_scores,axis=1)
plt.grid()#背景设置为网格线
plt.fill_between(train_sizes,train_scores_mean-train_scores_std,train_scores_mean+train_scores_std,alpha=0.1,color='r')
# plt.fill_between()函数会把模型准确性的平均值的上下方差的空间里用颜色填充。
plt.fill_between(train_sizes,test_scores_mean-test_scores_std,test_scores_mean+test_scores_std,alpha=0.1,color='g')
plt.plot(train_sizes,train_scores_mean,'o-',color='r',label='Training score')
# 然后用plt.plot()函数画出模型准确性的平均值
plt.plot(train_sizes,test_scores_mean,'o-',color='g',label='Cross_validation score')
plt.legend(loc='best')#显示图例
return plt
cv=ShuffleSplit(n_splits=10,test_size=0.2,random_state=0)
title='Learning Curve(degree={0},penalty={1})'
degrees=[1,2]
penalty='l1'
start=time.clock()
plt.figure(figsize=(12,4),dpi=144)
for i in range(len(degrees)):
plt.subplot(1,2,i+1)
plot_learning_curve(polynomial_model(degree=degrees[i],penalty=penalty),title.format(degrees[i],penalty),X,y,ylim=(0.8,1.01),cv=cv)
print('elaspe:{0:.6f}'.format(time.clock()-start))
输出如下:
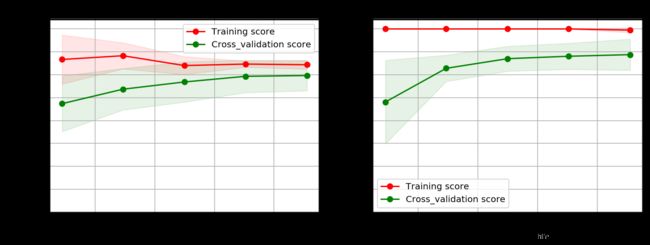
我们可以看到二项多项式特征的模型效果很好,训练集的预测率达到了100%,而且test集也没有出现过拟合的现象。
如果你想画出L2范式的学习曲线,只需要将penalty的值改为’l2’。
penalty='l2'
输出如下: