平面2R机器人(二连杆)运动学与动力学建模+附仿真模型
平面2R机器人运动学与动力学建模+附仿真模型
- 1 平面2R机器人概述
- 2 运动学建模
-
- 2.1 正运动学模型
- 2.2 逆运动学模型
- 2.3 机器人运动学仿真
- 3 动力学建模
-
- 3.1 计算动能
- 3.2 势能计算与动力学方程
- 3.3 动力学仿真
1 平面2R机器人概述
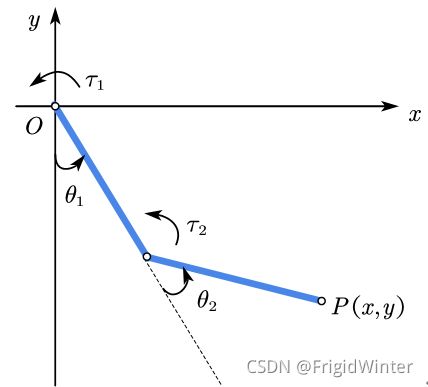
如图1所示为本文的研究本体——平面2R机器人。对参数进行如下定义:机器人广义坐标 θ 1 \theta _1 θ1为连杆1与 y y y轴负半轴的夹角,逆时针为正; θ 2 \theta _2 θ2为连杆2与连杆1延长线的夹角,逆时针为正;连杆1、2的关节力矩分别定义为 τ 1 \tau_1 τ1、 τ 2 \tau_2 τ2。设连杆质量均匀分布,长度都为 l l l,质量都为 M M M,末端执行器笛卡尔坐标为 P ( x , y ) P(x,y) P(x,y)。
2 运动学建模
2.1 正运动学模型
指数积方法的核心原理是基于运动旋量的指数积公式:
T A T ( θ ) = e [ V 1 ] θ 1 e [ V 2 ] θ 2 ⋯ e [ V n ] θ n T A T ( 0 ) _{\boldsymbol{T}}^{\boldsymbol{A}}\boldsymbol{T}\left( \boldsymbol{\theta } \right) =e^{\left[ \boldsymbol{V}_1 \right] \theta _1}e^{\left[ \boldsymbol{V}_2 \right] \theta _2}\cdots {e^{\left[ \boldsymbol{V}_n \right] \theta _n}}_{\boldsymbol{T}}^{\boldsymbol{A}}\boldsymbol{T}\left( 0 \right) TAT(θ)=e[V1]θ1e[V2]θ2⋯e[Vn]θnTAT(0)
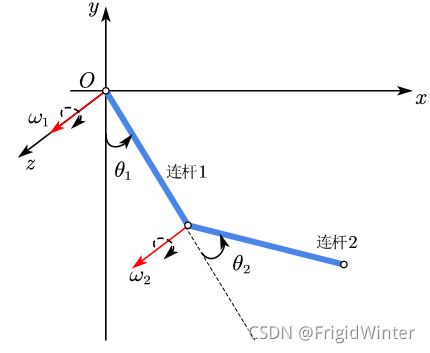
可以证明,连杆变换之积(DH法)等价于指数积。对平面2R机器人,确定各个关节轴线的线矢量如图2所示,不必建立连杆坐标系。
各轴线方向如下:
ω 1 = ω 2 = [ 0 0 1 ] , [ ω 1 ] = [ ω 2 ] = [ 0 − 1 0 1 0 0 0 0 0 ] \omega _1=\omega _2=\left[ \begin{array}{c} 0\\ 0\\ 1\\\end{array} \right] ,\mathrm{ }\left[ \omega _1 \right] =\left[ \omega _2 \right] =\left[ \begin{matrix} 0& -1& 0\\ 1& 0& 0\\ 0& 0& 0\\\end{matrix} \right] ω1=ω2=⎣⎡001⎦⎤,[ω1]=[ω2]=⎣⎡010−100000⎦⎤
取各个运动轴上的一点:
r 1 = [ 0 0 0 ] , r 2 = [ 0 − l 0 ] r_1=\left[ \begin{array}{c} 0\\ 0\\ 0\\\end{array} \right] ,\mathrm{ }r_2=\left[ \begin{array}{c} 0\\ -l\\ 0\\\end{array} \right] r1=⎣⎡000⎦⎤,r2=⎣⎡0−l0⎦⎤
可得各个运动旋量的指数形式
e [ V 1 ] θ 1 = [ cos θ 1 − sin θ 1 0 0 sin θ 1 cos θ 1 0 0 0 0 1 0 0 0 0 1 ] , e [ V 2 ] θ 2 = [ cos θ 2 − sin θ 2 0 − l sin θ 2 sin θ 2 cos θ 2 0 − l ( 1 − cos θ 2 ) 0 0 1 0 0 0 0 1 ] e^{\left[ \boldsymbol{V}_1 \right] \theta _1}=\left[ \begin{matrix} \cos \theta _1& -\sin \theta _1& 0& 0\\ \sin \theta _1& \cos \theta _1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\\end{matrix} \right] , e^{\left[ \boldsymbol{V}_2 \right] \theta _2}=\left[ \begin{matrix} \cos \theta _2& -\sin \theta _2& 0& -l\sin \theta _2\\ \sin \theta _2& \cos \theta _2& 0& -l\left( 1-\cos \theta _2 \right)\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\\end{matrix} \right] e[V1]θ1=⎣⎢⎢⎡cosθ1sinθ100−sinθ1cosθ10000100001⎦⎥⎥⎤,e[V2]θ2=⎣⎢⎢⎡cosθ2sinθ200−sinθ2cosθ2000010−lsinθ2−l(1−cosθ2)01⎦⎥⎥⎤
关节变量 θ = [ θ 1 θ 2 ] \boldsymbol{\theta }=\left[ \begin{matrix} \theta _1& \theta _2\\\end{matrix} \right] θ=[θ1θ2]为0时即为初始位姿:
T B T ( 0 ) = [ 1 0 0 0 0 1 0 − 2 l 0 0 1 0 0 0 0 1 ] _{T}^{B}\boldsymbol{T}\left( 0 \right) =\left[ \begin{matrix} 1& 0& 0& 0\\ 0& 1& 0& -2l\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\\end{matrix} \right] TBT(0)=⎣⎢⎢⎡1000010000100−2l01⎦⎥⎥⎤
所以由 T B T ( θ ) = e [ V 1 ] θ 1 e [ V 2 ] θ 2 T S T ( 0 ) _{T}^{B}\boldsymbol{T}\left( \boldsymbol{\theta } \right) =e^{\left[ \boldsymbol{V}_1 \right] \theta _1}e^{\left[ \boldsymbol{V}_2 \right] \theta _2}\!\:_{T}^{S}\boldsymbol{T}\left( 0 \right) TBT(θ)=e[V1]θ1e[V2]θ2TST(0)即得
T B T ( θ ) = [ cos ( θ 1 + θ 2 ) − sin ( θ 1 + θ 2 ) 0 l sin ( θ 1 + θ 2 ) + l sin θ 1 sin ( θ 1 + θ 2 ) cos ( θ 1 + θ 2 ) 0 − l cos ( θ 1 + θ 2 ) − l cos θ 1 0 0 1 0 0 0 0 1 ] _{T}^{B}\boldsymbol{T}\left( \boldsymbol{\theta } \right) =\left[ \begin{matrix} \cos \left( \theta _1+\theta _2 \right)& -\sin \left( \theta _1+\theta _2 \right)& 0& l\sin \left( \theta _1+\theta _2 \right) +l\sin \theta _1\\ \sin \left( \theta _1+\theta _2 \right)& \cos \left( \theta _1+\theta _2 \right)& 0& -l\cos \left( \theta _1+\theta _2 \right) -l\cos \theta _1\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\\end{matrix} \right] TBT(θ)=⎣⎢⎢⎡cos(θ1+θ2)sin(θ1+θ2)00−sin(θ1+θ2)cos(θ1+θ2)000010lsin(θ1+θ2)+lsinθ1−lcos(θ1+θ2)−lcosθ101⎦⎥⎥⎤
可以验证,基于运动旋量法的机器人正运动学模型,与基于D-H法的正运动学模型相同,可交叉验证正运动学模型的理论正确性。
2.2 逆运动学模型
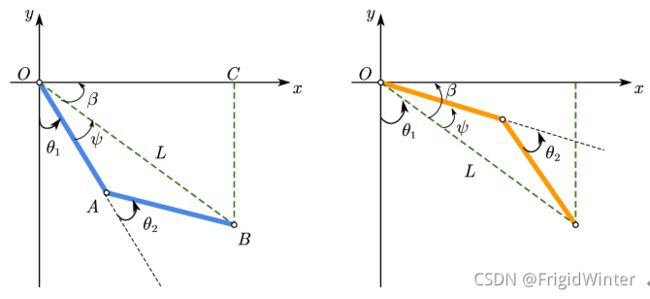
对于位形一,在 Δ O A B \varDelta OAB ΔOAB中运用余弦定理可得 2 l 2 cos ( π − θ 2 ) = l 2 + l 2 − L 2 2l^2\cos \left( \pi -\theta _2 \right) =l^2+l^2-L^2 2l2cos(π−θ2)=l2+l2−L2,其中 L 2 = x 2 + y 2 L^2=x^2+y^2 L2=x2+y2,显然末端执行器坐标需要满足 0 < x 2 + y 2 ⩽ 2 l 0<\sqrt{x^2+y^2}\leqslant 2l 0<x2+y2⩽2l
解得:
θ 2 = a r c cos ( x 2 + y 2 2 l 2 − 1 ) \theta _2=\mathrm{arc}\cos \left( \frac{x^2+y^2}{2l^2}-1 \right) θ2=arccos(2l2x2+y2−1)
有两个解,位形一对应正解,位形二对应负解。
同样在 Δ O A B \varDelta OAB ΔOAB中运用余弦定理可得
ψ = a r c cos ( x 2 + y 2 2 l ) \psi =\mathrm{arc}\cos \left( \frac{\sqrt{x^2+y^2}}{2l} \right) ψ=arccos(2lx2+y2)
为方便起见,这里总是取 ψ \psi ψ的正解。再根据
β = ∣ a r c tan ( y x ) ∣ \beta =\left| \mathrm{arc}\tan \left( \frac{y}{x} \right) \right| β=∣∣∣arctan(xy)∣∣∣
可得位形一下的关节参数 θ 1 = π 2 − ( β + ψ ) \theta _1=\frac{\pi}{2}-\left( \beta +\psi \right) θ1=2π−(β+ψ)。当机械臂运动到其他象限时同理,求得平面2R机器人运动学反解为:
{ θ 1 = π 2 − ( β ± ψ ) , θ 2 > 0 时取 + θ 1 = π 2 + ( β ± ψ ) , θ 2 > 0 时取 − θ 1 = 3 π 2 − ( β ± ψ ) , θ 2 > 0 时取 + θ 1 = 3 π 2 + ( β ± ψ ) , θ 2 > 0 时取 − \begin{cases} \theta _1=\frac{\pi}{2}-\left( \beta \pm \psi \right) , \theta _2>0\text{时取}+\\ \theta _1=\frac{\pi}{2}+\left( \beta \pm \psi \right) , \theta _2>0\text{时取}-\\ \theta _1=\frac{3\pi}{2}-\left( \beta \pm \psi \right) , \theta _2>0\text{时取}+\\ \theta _1=\frac{3\pi}{2}+\left( \beta \pm \psi \right) , \theta _2>0\text{时取}-\\\end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧θ1=2π−(β±ψ),θ2>0时取+θ1=2π+(β±ψ),θ2>0时取−θ1=23π−(β±ψ),θ2>0时取+θ1=23π+(β±ψ),θ2>0时取−
2.3 机器人运动学仿真
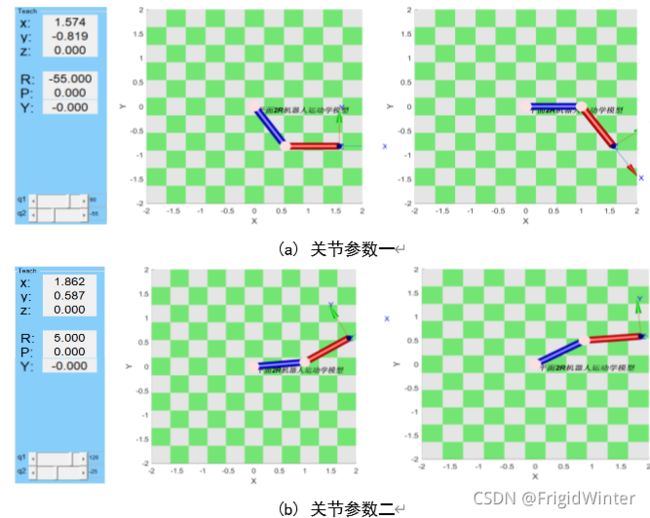
基于Matlab Robotics工具箱进行平面2R机器人的运动学仿真验证。验证过程如下:分别选取位于四个象限的关节参数
[ θ 1 θ 2 ] = [ 35 ° 55 ° ] , [ θ 1 θ 2 ] = [ 95 ° 25 ° ] , [ θ 1 θ 2 ] = [ 230 ° 20 ° ] , [ θ 1 θ 2 ] = [ 300 ° 70 ° ] \left[ \begin{array}{c} \theta _1\\ \theta _2\\\end{array} \right] =\left[ \begin{array}{c} 35\degree\\ 55\degree\\\end{array} \right] , \left[ \begin{array}{c} \theta _1\\ \theta _2\\\end{array} \right] =\left[ \begin{array}{c} 95\degree\\ 25\degree\\\end{array} \right] , \left[ \begin{array}{c} \theta _1\\ \theta _2\\\end{array} \right] =\left[ \begin{array}{c} 230\degree\\ 20\degree\\\end{array} \right] , \left[ \begin{array}{c} \theta _1\\ \theta _2\\\end{array} \right] =\left[ \begin{array}{c} 300\degree\\ 70\degree\\\end{array} \right] [θ1θ2]=[35°55°],[θ1θ2]=[95°25°],[θ1θ2]=[230°20°],[θ1θ2]=[300°70°]
进行正运动的验证,而后基于四组末端执行器的坐标进行运动学反解,得到该坐标下的另一个位形对应的关节参数,将该参数代入Matlab机器人模型,验证此时末端执行器的坐标是否与位形一下的重合。将四组参数分别代入上式,得到
[ x y ] = [ 1.57 − 0.82 ] , [ x y ] = [ 1.86 0.59 ] , [ x y ] = [ − 1.71 0.99 ] , [ x y ] = [ − 0.69 − 1.48 ] \left[ \begin{array}{c} x\\ y\\\end{array} \right] =\left[ \begin{array}{c} 1.57\\ -0.82\\\end{array} \right] , \left[ \begin{array}{c} x\\ y\\\end{array} \right] =\left[ \begin{array}{c} 1.86\\ 0.59\\\end{array} \right] , \left[ \begin{array}{c} x\\ y\\\end{array} \right] =\left[ \begin{array}{c} -1.71\\ 0.99\\\end{array} \right] , \left[ \begin{array}{c} x\\ y\\\end{array} \right] =\left[ \begin{array}{c} -0.69\\ -1.48\\\end{array} \right] [xy]=[1.57−0.82],[xy]=[1.860.59],[xy]=[−1.710.99],[xy]=[−0.69−1.48]
将这四组笛卡尔坐标值代入式,得到另一位形的关节参数值
[ θ 1 θ 2 ] = [ 90 ° − 55 ° ] , [ θ 1 θ 2 ] = [ 120 ° − 25 ° ] , [ θ 1 θ 2 ] = [ 249 ° − 20 ° ] , [ θ 1 θ 2 ] = [ 10 ° − 70 ° ] \left[ \begin{array}{c} \theta _1\\ \theta _2\\\end{array} \right] =\left[ \begin{array}{c} 90\degree\\ -55\degree\\\end{array} \right] , \left[ \begin{array}{c} \theta _1\\ \theta _2\\\end{array} \right] =\left[ \begin{array}{c} 120\degree\\ -25\degree\\\end{array} \right] , \left[ \begin{array}{c} \theta _1\\ \theta _2\\\end{array} \right] =\left[ \begin{array}{c} 249\degree\\ -20\degree\\\end{array} \right] , \left[ \begin{array}{c} \theta _1\\ \theta _2\\\end{array} \right] =\left[ \begin{array}{c} 10\degree\\ -70\degree\\\end{array} \right] [θ1θ2]=[90°−55°],[θ1θ2]=[120°−25°],[θ1θ2]=[249°−20°],[θ1θ2]=[10°−70°]
3 动力学建模
3.1 计算动能
取定连杆上一质量微元 d m \mathrm{d}m dm,其位置坐标为 ( x , y ) (x,y) (x,y),采用极坐标表示即为
连杆I { x = r sin θ 1 y = − r cos θ 1 连杆II { x = l sin θ 1 + r sin ( θ 1 + θ 2 ) y = − l cos θ 1 − r cos ( θ 1 + θ 2 ) \text{连杆I}\begin{cases} x=r\sin \theta _1\\ y=-r\cos \theta _1\\\end{cases}\,\, \text{连杆II}\begin{cases} x=l\sin \theta _1+r\sin \left( \theta _1+\theta _2 \right)\\ y=-l\cos \theta _1-r\cos \left( \theta _1+\theta _2 \right)\\\end{cases} 连杆I{ x=rsinθ1y=−rcosθ1连杆II{ x=lsinθ1+rsin(θ1+θ2)y=−lcosθ1−rcos(θ1+θ2)
对时间求导,得到
连杆I { x ˙ = r θ ˙ 1 cos θ 1 y ˙ = r θ ˙ 1 sin θ 1 连杆II { x ˙ = l θ ˙ 1 cos θ 1 + r ( θ ˙ 1 + θ ˙ 2 ) cos ( θ 1 + θ 2 ) y ˙ = l θ ˙ 1 sin θ 1 + r ( θ ˙ 1 + θ ˙ 2 ) sin ( θ 1 + θ 2 ) \text{连杆I}\begin{cases} \dot{x}=r\dot{\theta}_1\cos \theta _1\\ \dot{y}=r\dot{\theta}_1\sin \theta _1\\\end{cases}\,\, \text{连杆II}\begin{cases} \dot{x}=l\dot{\theta}_1\cos \theta _1+r\left( \dot{\theta}_1+\dot{\theta}_2 \right) \cos \left( \theta _1+\theta _2 \right)\\ \dot{y}=l\dot{\theta}_1\sin \theta _1+r\left( \dot{\theta}_1+\dot{\theta}_2 \right) \sin \left( \theta _1+\theta _2 \right)\\\end{cases} 连杆I{ x˙=rθ˙1cosθ1y˙=rθ˙1sinθ1连杆II⎩⎨⎧x˙=lθ˙1cosθ1+r(θ˙1+θ˙2)cos(θ1+θ2)y˙=lθ˙1sinθ1+r(θ˙1+θ˙2)sin(θ1+θ2)
所以质量微元速度为
{ 连杆I: v 1 2 = x ˙ 2 + y ˙ 2 = r 2 θ ˙ 1 2 连杆II: v 2 2 = x ˙ 2 + y ˙ 2 = l 2 θ ˙ 1 2 + r 2 ( θ ˙ 1 + θ ˙ 2 ) 2 + 2 l r θ ˙ 1 ( θ ˙ 1 + θ ˙ 2 ) cos θ 2 \begin{cases} \text{连杆I:}v_{1}^{2}=\dot{x}^2+\dot{y}^2=r^2\dot{\theta}_{1}^{2}\\ \text{连杆II:}v_{2}^{2}=\dot{x}^2+\dot{y}^2=l^2\dot{\theta}_{1}^{2}+r^2\left( \dot{\theta}_1+\dot{\theta}_2 \right) ^2+2lr\dot{\theta}_1\left( \dot{\theta}_1+\dot{\theta}_2 \right) \cos \theta _2\\\end{cases} ⎩⎨⎧连杆I:v12=x˙2+y˙2=r2θ˙12连杆II:v22=x˙2+y˙2=l2θ˙12+r2(θ˙1+θ˙2)2+2lrθ˙1(θ˙1+θ˙2)cosθ2
因此机器人动能为
E k = 1 2 ∫ m d m ⋅ v 2 = 1 2 ρ [ ∫ 0 l r 2 θ ˙ 1 2 d r + ∫ 0 l l 2 θ ˙ 1 2 + r 2 ( θ ˙ 1 + θ ˙ 2 ) 2 + 2 l r θ ˙ 1 ( θ ˙ 1 + θ ˙ 2 ) cos θ 2 d r ] = 1 2 m l 2 [ ( 5 3 + cos θ 2 ) θ ˙ 1 2 + ( 2 3 + cos θ 2 ) θ ˙ 1 θ ˙ 2 + 1 3 θ ˙ 2 2 ] E_k=\frac{1}{2}\int_m{\mathrm{d}m\cdot v^2}\\=\frac{1}{2}\rho \left[ \int_0^l{r^2\dot{\theta}_{1}^{2}\mathrm{d}r}+\int_0^l{l^2\dot{\theta}_{1}^{2}+r^2\left( \dot{\theta}_1+\dot{\theta}_2 \right) ^2+2lr\dot{\theta}_1\left( \dot{\theta}_1+\dot{\theta}_2 \right) \cos \theta _2\mathrm{d}r} \right] \\=\frac{1}{2}ml^2\left[ \left( \frac{5}{3}+\cos \theta _2 \right) \dot{\theta}_{1}^{2}+\left( \frac{2}{3}+\cos \theta _2 \right) \dot{\theta}_1\dot{\theta}_2+\frac{1}{3}\dot{\theta}_{2}^{2} \right] Ek=21∫mdm⋅v2=21ρ[∫0lr2θ˙12dr+∫0ll2θ˙12+r2(θ˙1+θ˙2)2+2lrθ˙1(θ˙1+θ˙2)cosθ2dr]=21ml2[(35+cosθ2)θ˙12+(32+cosθ2)θ˙1θ˙2+31θ˙22]
3.2 势能计算与动力学方程
以基坐标系 x x x轴为零势能面,则系统总势能为
E p = − m g l [ 3 2 cos θ 1 + 1 2 cos ( θ 1 + θ 2 ) ] E_p=-mgl\left[ \frac{3}{2}\cos \theta _1+\frac{1}{2}\cos \left( \theta _1+\theta _2 \right) \right] Ep=−mgl[23cosθ1+21cos(θ1+θ2)]
对于任何机械系统.拉格朗日函数定义为系统总动能和势能之差,即
L = E k − E p = 1 2 m l 2 [ ( 5 3 + cos θ 2 ) θ ˙ 1 2 + ( 2 3 + cos θ 2 ) θ ˙ 1 θ ˙ 2 + 1 3 θ ˙ 2 2 ] + m g l [ 3 2 cos θ 1 + 1 2 cos ( θ 1 + θ 2 ) ] L=E_k-E_p\\=\frac{1}{2}ml^2\left[ \left( \frac{5}{3}+\cos \theta _2 \right) \dot{\theta}_{1}^{2}+\left( \frac{2}{3}+\cos \theta _2 \right) \dot{\theta}_1\dot{\theta}_2+\frac{1}{3}\dot{\theta}_{2}^{2} \right] +mgl\left[ \frac{3}{2}\cos \theta _1+\frac{1}{2}\cos \left( \theta _1+\theta _2 \right) \right] L=Ek−Ep=21ml2[(35+cosθ2)θ˙12+(32+cosθ2)θ˙1θ˙2+31θ˙22]+mgl[23cosθ1+21cos(θ1+θ2)]
基于拉格朗日函数可得
{ ∂ L ∂ θ 1 = − m g l [ 3 2 sin θ 1 + 1 2 sin ( θ 1 + θ 2 ) ] ∂ L ∂ θ ˙ 1 = 1 2 m l 2 [ ( 10 3 + 2 cos θ 2 ) θ ˙ 1 + ( 2 3 + cos θ 2 ) θ ˙ 2 ] d d t ( ∂ L ∂ θ ˙ 1 ) = 1 2 m l 2 [ ( 10 3 + 2 cos θ 2 ) θ ¨ 1 − 2 θ ˙ 1 θ ˙ 2 sin θ 2 + ( 2 3 + cos θ 2 ) θ ¨ 2 − θ ˙ 2 2 sin θ 2 ] \begin{cases} \frac{\partial L}{\partial \theta _1}=-mgl\left[ \frac{3}{2}\sin \theta _1+\frac{1}{2}\sin \left( \theta _1+\theta _2 \right) \right]\\ \frac{\partial L}{\partial \dot{\theta}_1}=\frac{1}{2}ml^2\left[ \left( \frac{10}{3}+2\cos \theta _2 \right) \dot{\theta}_1+\left( \frac{2}{3}+\cos \theta _2 \right) \dot{\theta}_2 \right]\\ \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial \dot{\theta}_1} \right) =\frac{1}{2}ml^2\left[ \left( \frac{10}{3}+2\cos \theta _2 \right) \ddot{\theta}_1-2\dot{\theta}_1\dot{\theta}_2\sin \theta _2+\left( \frac{2}{3}+\cos \theta _2 \right) \ddot{\theta}_2-\dot{\theta}_{2}^{2}\sin \theta _2 \right]\\\end{cases} ⎩⎪⎪⎨⎪⎪⎧∂θ1∂L=−mgl[23sinθ1+21sin(θ1+θ2)]∂θ˙1∂L=21ml2[(310+2cosθ2)θ˙1+(32+cosθ2)θ˙2]dtd(∂θ˙1∂L)=21ml2[(310+2cosθ2)θ¨1−2θ˙1θ˙2sinθ2+(32+cosθ2)θ¨2−θ˙22sinθ2]
{ ∂ L ∂ θ 2 = − 1 2 m g l sin ( θ 1 + θ 2 ) − 1 2 m l 2 ( θ ˙ 1 2 + θ ˙ 1 θ ˙ 2 ) sin θ 2 ∂ L ∂ θ ˙ 2 = 1 2 m l 2 [ ( 2 3 + cos θ 2 ) θ ˙ 1 + 2 3 θ ˙ 2 ] d d t ( ∂ L ∂ θ ˙ 2 ) = 1 2 m l 2 [ ( 2 3 + cos θ 2 ) θ ¨ 1 − θ ˙ 1 θ ˙ 2 sin θ 2 + 2 3 θ ¨ 2 ] \begin{cases} \frac{\partial L}{\partial \theta _2}=-\frac{1}{2}mgl\sin \left( \theta _1+\theta _2 \right) -\frac{1}{2}ml^2\left( \dot{\theta}_{1}^{2}+\dot{\theta}_1\dot{\theta}_2 \right) \sin \theta _2\\ \frac{\partial L}{\partial \dot{\theta}_2}=\frac{1}{2}ml^2\left[ \left( \frac{2}{3}+\cos \theta _2 \right) \dot{\theta}_1+\frac{2}{3}\dot{\theta}_2 \right]\\ \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial \dot{\theta}_2} \right) =\frac{1}{2}ml^2\left[ \left( \frac{2}{3}+\cos \theta _2 \right) \ddot{\theta}_1-\dot{\theta}_1\dot{\theta}_2\sin \theta _2+\frac{2}{3}\ddot{\theta}_2 \right]\\\end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧∂θ2∂L=−21mglsin(θ1+θ2)−21ml2(θ˙12+θ˙1θ˙2)sinθ2∂θ˙2∂L=21ml2[(32+cosθ2)θ˙1+32θ˙2]dtd(∂θ˙2∂L)=21ml2[(32+cosθ2)θ¨1−θ˙1θ˙2sinθ2+32θ¨2]
根据拉格朗日方程
{ τ 1 = d d t ( ∂ L ∂ θ ˙ 1 ) − ∂ L ∂ θ 1 τ 2 = d d t ( ∂ L ∂ θ ˙ 2 ) − ∂ L ∂ θ 2 \begin{cases} \tau _1=\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial \dot{\theta}_1} \right) -\frac{\partial L}{\partial \theta _1}\\ \tau _2=\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\partial L}{\partial \dot{\theta}_2} \right) -\frac{\partial L}{\partial \theta _2}\\\end{cases} ⎩⎨⎧τ1=dtd(∂θ˙1∂L)−∂θ1∂Lτ2=dtd(∂θ˙2∂L)−∂θ2∂L
求得机器人动力学模型为
τ = D 1 ( θ ) θ ¨ ⏟ 惯性力项 + D 2 ( θ ) θ ˙ 2 ⏟ 向心力项 + D 3 ( θ ) θ ˙ i j ⏟ 科氏力项 + D 4 ( θ ) ⏟ 重力项 ⇔ [ τ 1 τ 2 ] = D 1 ( θ ) [ θ ¨ 1 θ ¨ 2 ] + D 2 ( θ ) [ θ ˙ 1 2 θ ˙ 2 2 ] + D 3 ( θ ) [ θ ˙ 1 θ ˙ 2 θ ˙ 1 θ ˙ 2 ] + D 4 ( θ ) \boldsymbol{\tau }=\underset{\text{惯性力项}}{\underbrace{\boldsymbol{D}_1\left( \boldsymbol{\theta } \right) \boldsymbol{\ddot{\theta}}}}+\underset{\text{向心力项}}{\underbrace{\boldsymbol{D}_2\left( \boldsymbol{\theta } \right) \boldsymbol{\dot{\theta}}^2}}+\underset{\text{科氏力项}}{\underbrace{\boldsymbol{D}_3\left( \boldsymbol{\theta } \right) \boldsymbol{\dot{\theta}}_{ij}}}+\underset{\text{重力项}}{\underbrace{\boldsymbol{D}_4\left( \boldsymbol{\theta } \right) }}\\\Leftrightarrow \left[ \begin{array}{c} \tau _1\\ \tau _2\\\end{array} \right] =\boldsymbol{D}_1\left( \boldsymbol{\theta } \right) \left[ \begin{array}{c} \ddot{\theta}_1\\ \ddot{\theta}_2\\\end{array} \right] +\boldsymbol{D}_2\left( \boldsymbol{\theta } \right) \left[ \begin{array}{c} \dot{\theta}_{1}^{2}\\ \dot{\theta}_{2}^{2}\\\end{array} \right] +\boldsymbol{D}_3\left( \boldsymbol{\theta } \right) \left[ \begin{array}{c} \dot{\theta}_1\dot{\theta}_2\\ \dot{\theta}_1\dot{\theta}_2\\\end{array} \right] +\boldsymbol{D}_4\left( \boldsymbol{\theta } \right) τ=惯性力项 D1(θ)θ¨+向心力项 D2(θ)θ˙2+科氏力项 D3(θ)θ˙ij+重力项 D4(θ)⇔[τ1τ2]=D1(θ)[θ¨1θ¨2]+D2(θ)[θ˙12θ˙22]+D3(θ)[θ˙1θ˙2θ˙1θ˙2]+D4(θ)
其中
{ D 1 ( θ ) = m l 2 [ 5 3 + cos θ 2 1 3 + 1 2 cos θ 2 1 3 + 1 2 cos θ 2 1 3 ] D 2 ( θ ) = m l 2 [ 0 − 1 2 sin θ 2 1 2 sin θ 2 0 ] D 3 ( θ ) = m l 2 [ − sin θ 2 0 0 0 ] D 4 ( θ ) = m g l [ 3 2 sin θ 1 + 1 2 sin ( θ 1 + θ 2 ) 1 2 sin ( θ 1 + θ 2 ) ] \begin{cases} \boldsymbol{D}_1\left( \boldsymbol{\theta } \right) =ml^2\left[ \begin{matrix} \frac{5}{3}+\cos \theta _2& \frac{1}{3}+\frac{1}{2}\cos \theta _2\\ \frac{1}{3}+\frac{1}{2}\cos \theta _2& \frac{1}{3}\\\end{matrix} \right]\\ \boldsymbol{D}_2\left( \boldsymbol{\theta } \right) =ml^2\left[ \begin{matrix} 0& -\frac{1}{2}\sin \theta _2\\ \frac{1}{2}\sin \theta _2& 0\\\end{matrix} \right]\\ \boldsymbol{D}_3\left( \boldsymbol{\theta } \right) =ml^2\left[ \begin{matrix} -\sin \theta _2& 0\\ 0& 0\\\end{matrix} \right]\\ \boldsymbol{D}_4\left( \boldsymbol{\theta } \right) =mgl\left[ \begin{array}{c} \frac{3}{2}\sin \theta _1+\frac{1}{2}\sin \left( \theta _1+\theta _2 \right)\\ \frac{1}{2}\sin \left( \theta _1+\theta _2 \right)\\\end{array} \right]\\\end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧D1(θ)=ml2[35+cosθ231+21cosθ231+21cosθ231]D2(θ)=ml2[021sinθ2−21sinθ20]D3(θ)=ml2[−sinθ2000]D4(θ)=mgl[23sinθ1+21sin(θ1+θ2)21sin(θ1+θ2)]
3.3 动力学仿真
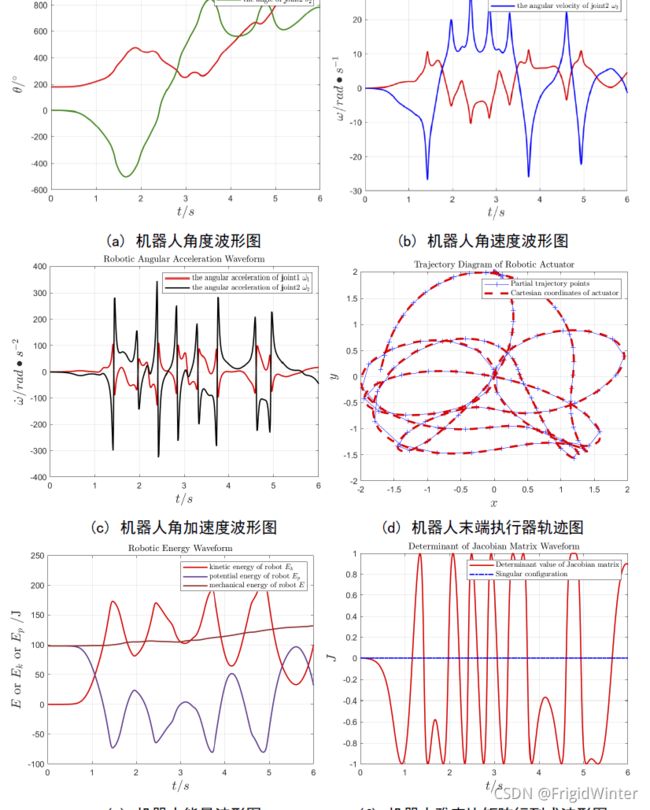
初始状态为 [ θ 1 θ 2 ] = [ 180 ° 0 ° ] \left[ \begin{array}{c} \theta _1\\ \theta _2\\\end{array} \right] =\left[ \begin{array}{c} 180\degree\\ 0\degree\\\end{array} \right] [θ1θ2]=[180°0°]、 [ θ ˙ 1 θ ˙ 2 ] = [ 0 0 ] \left[ \begin{array}{c} \dot{\theta}_1\\ \dot{\theta}_2\\\end{array} \right] =\left[ \begin{array}{c} 0\\ 0\\\end{array} \right] [θ˙1θ˙2]=[00],输入力矩为 [ τ 1 τ 2 ] = [ 2 0.5 ] \left[ \begin{array}{c} \tau _1\\ \tau _2\\\end{array} \right] =\left[ \begin{array}{c} 2\\ 0.5\\\end{array} \right] [τ1τ2]=[20.5] 该初始条件下,平面2R机器人的角度、角速度、角加速度、能量、雅克比矩阵行列式数值波形图以及机器人末端执行器运动轨迹图如图所示