AI-支持向量机分类预测

基于支持向量机的分类预测

1.简介

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机，其决策边界是对学习样本求解的最大边距超平面。
SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，*即从决策边界到各个数据集的距离越大，分类操作出错率越小。*可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

• 当训练样本线性可分时，通过硬间隔最大化，学习一个线性可分支持向量机。
• 当训练样本近似线性可分时，通过软间隔最大化，学习一个线性支持向量机。
• 当训练样本线性不可分时，通过核技巧和软间隔最大化，学习一个非线性支持向量机。

2. 学习重点

3.基本原理

3.1 支持向量

3.1.1 线性可分性

什么是线性可分？

• 决策边界：在具有两个类的统计分类问题中，决策边界或决策表面是超曲面，其将基础向量空间划分为两个集合。如果决策表面是超平面，那么分类问题是线性的，并且类是线性可分的。
• 超平面：超平面是n维欧氏空间中余维度等于一的线性子空间，也就是必须是(n-1)维度。

换一种简单的说法，就是在二分空间上，有两类点被一条直线完全分开叫做线性可分。

3.1.2 最大间隔超平面

简单点说：

为了使这个超平面更具鲁棒性，会去找最佳超平面，以最大间隔把两类样本分开的超平面，也称之为最大间隔超平面。

• 两类样本分别分割在该超平面的两侧；
• 两侧距离超平面最近的样本点到超平面的距离被最大化了。

3.1.3 支持向量

样本中距离超平面最近的一些点就叫作支持向量，如下图所示

3.1.3 SVM最优化

SVM 想要的就是找到各类样本点到超平面的距离最远，也就是找到最大间隔超平面。任意超平面可以用下面这个线性方程来描述：

如上图所示：

• 根据支持向量的定义知道，支持向量到超平面的距离为 d，其他点到超平面的距离大于 d。
• 而在超平面两边的点，一类是为正类，一类为负类，各自离超平面距离大于d则可表示为：
  
  
  
  注：这里的“s.t.”意为 subject to，使满足。

3.2 对偶问题

3.2.1 拉格朗日乘数法

在数学最优问题中，拉格朗日乘数法是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题，其变量不受任何约束。这种方法引入了一种新的标量未知数，即拉格朗日乘数：约束方程的梯度（gradient）的线性组合里每个向量的系数。

A.等式约束优化问题：

B. 不等式约束优化问题
现在面对的是不等式优化问题，针对这种情况其主要思想是将不等式约束条件转变为等式约束条件，引入松弛变量，将松弛变量也是为优化变量，即
不等式约束优化⇒ 引入松弛变量（优化变量）⇒ 等式约束优化 ⇒ 引入Lagrange乘子（优化变量）⇒ 无约束优化（将Lagrange函数对所有优化变量求偏导令其值为零）

这个式子告诉了什么事情呢？（下面依旧半懂状态，需要琢磨）

或另一种方程解：

3.2.2 强对偶性

3.3 SVM优化

即

没法一次只变动一个参数。所以选择了一次选择两个参数。具体步骤为：

3.4 软间隔

前面我们是假定所有的训练样本在样本空间或特征空间中是严格线性可分的，即存在一个超平面能把不同类的样本完全分开，然而现实任务中很难确定这样的超平面（不管是线性超平面还是经过核变换到高维空间的超平面），所以引入松弛变量，允许一些样本出错，但我们希望出错的样本越少越好，所以松弛变量也有限制（注：公式中的松弛变量不是单单一个数，每个样本都有对应的松弛变量）。引入松弛变量的间隔问题成为软间隔。

3.4.2 优化目标及求解

3.5 核函数

3.5.1 线性不可分

刚刚讨论的硬间隔和软间隔都是在说样本的完全线性可分或者大部分样本点的线性可分。而现实任务中很可能遇到这样的情况，即不存在一个能够正确划分两个类别样本的超平面，对这样的问题，可以将样本从原始空间映射到一个更高维的特征空间中，使得样本在这个特征空间中线性可分。数学上可以证明，如果原始空间是有限维，即属性数有限，则一定存在一个高维特征空间使样本可分。

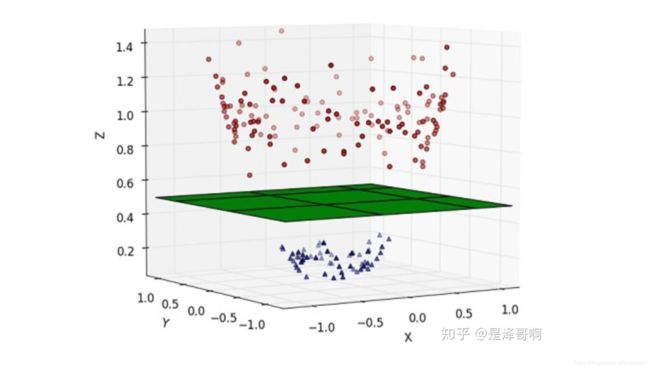
对于在有限维度向量空间中线性不可分的样本，我们将其映射到更高维度的向量空间里，再通过间隔最大化的方式，学习得到支持向量机，就是非线性 SVM。

3.5.2 核函数的作用

为什么要有核函数的呢？

这是因为低维空间映射到高维空间后维度可能会很大，如果将全部样本的点乘全部计算好，这样的计算量太大了。

然后在进行内积计算，才能与多项式核函数达到相同的效果。

可见核函数的引入一方面减少了我们计算量，另一方面也减少了我们存储数据的内存使用量。

3.5.3 常见核函数

这三个常用的核函数中只有高斯核函数是需要调参的。

3.6 优缺点

优点

• 有严格的数学理论支持，可解释性强，不依靠统计方法，从而简化了通常的分类和回归问题；
• 能找出对任务至关重要的关键样本（即：支持向量）；
• 采用核技巧之后，可以处理非线性分类/回归任务；
• 最终决策函数只由少数的支持向量所确定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了“维数灾难”。

缺点

因此，支持向量机目前只适合小批量样本的任务，无法适应百万甚至上亿样本的任务。

4. Demo实践

import numpy as np 
import matplotlib.pyplot as plt
import seaborn as sns
## 导入逻辑回归模型函数
from sklearn  import svm

## 构造数据集
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]])
y_label = np.array([0, 0, 0, 1, 1, 1])

## 调用SVC模型 （支持向量机分类）
svc = svm.SVC(kernel='linear')

## 用SVM模型拟合构造的数据集
svc = svc.fit(x_fearures, y_label) 

## 查看其对应模型的w
print('the weight of Logistic Regression:',svc.coef_)

## 查看其对应模型的w0
print('the intercept(w0) of Logistic Regression:',svc.intercept_)

## 模型预测
y_train_pred = svc.predict(x_fearures)
print('The predction result:',y_train_pred)
#The predction result: [0 0 0 1 1 1]
# 最佳函数
x_range = np.linspace(-3, 3)

#结合SVM的距离公式
w = svc.coef_[0]
a = -w[0] / w[1]
y_3 = a*x_range - (svc.intercept_[0]) / w[1]
'''案例比较简单，以严格分类作为案例讲述，效果自然比较好'''
# 可视化决策边界
plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=30, cmap='viridis')
plt.plot(x_range, y_3, '-c')
plt.show()

上述只是一个简单的样本，告知SVM可以做什么，就是简单的二分类案例。下面稍微切入正题，代入SVM解决三种分类问题，即支持向量，软间隔和核函数。

5. 支持向量机代码介绍

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
%matplotlib inline

# 画图
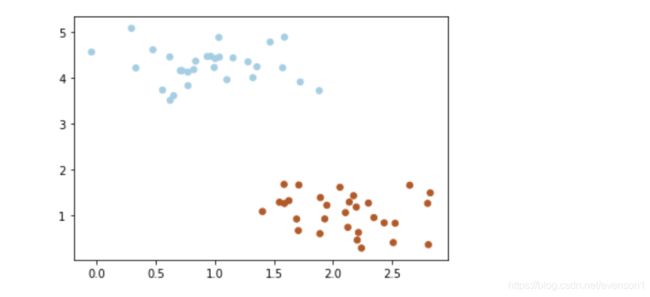
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)

### 画散点图及对应分类器
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)

x_fit = np.linspace(0, 3)
# 画函数
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
y_2 = -0.3 * x_fit + 3
plt.plot(x_fit, y_2, '-k')

问：两个分类器哪个更好？

为了判断好坏，我们需要引入一个准则：好的分类器不仅仅是能够很好的分开已有的数据集，还能对未知数据集进行两个的划分。即距离分类器越远越能说明类别区分明确—最大间隔。

假设有一个新的数据代入（3,2.8）

# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
plt.scatter([3], [2.8], c='#cccc00', marker='<', s=30, cmap=plt.cm.Paired)

x_fit = np.linspace(0, 3)

# 画函数
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
y_2 = -0.3 * x_fit + 3
plt.plot(x_fit, y_2, '-k')

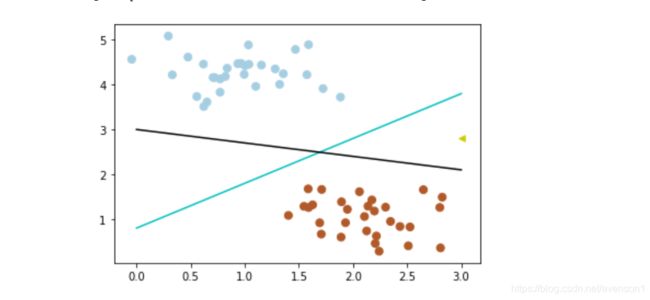
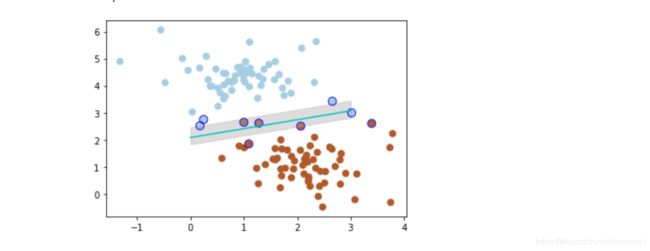
可以看到，上述的黑线就不满足分类的情况了，因为在已知的数据集中，黑色比蓝色离最大间隔更遥远。
加粗对应线段，查看对应的间隔。

### 加粗线段查看对应间隔
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)

x_fit = np.linspace(0, 3)

# 画函数
y_1 = 1 * x_fit + 0.8
plt.plot(x_fit, y_1, '-c')
# 画边距
plt.fill_between(x_fit, y_1 - 0.6, y_1 + 0.6, edgecolor='none', color='#AAAAAA', alpha=0.4)

y_2 = -0.3 * x_fit + 3
plt.plot(x_fit, y_2, '-k')
plt.fill_between(x_fit, y_2 - 0.4, y_2 + 0.4, edgecolor='none', color='#AAAAAA', alpha=0.4)

暂时选择蓝色最为分类器，但是不一定是最优，所以引入SVM求最优。

from sklearn.svm import SVC
# SVM 函数
clf = SVC(kernel='linear')
clf.fit(X, y)

# 最佳函数
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a*x_fit - (clf.intercept_[0]) / w[1]

# 最大边距 下届
b_down = clf.support_vectors_[0]
y_down = a* x_fit + b_down[1] - a * b_down[0]
# 最大边距 上届
b_up = clf.support_vectors_[-1]
y_up = a* x_fit + b_up[1] - a * b_up[0]

# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画函数
plt.plot(x_fit, y_3, '-c')
# 画边距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 画支持向量
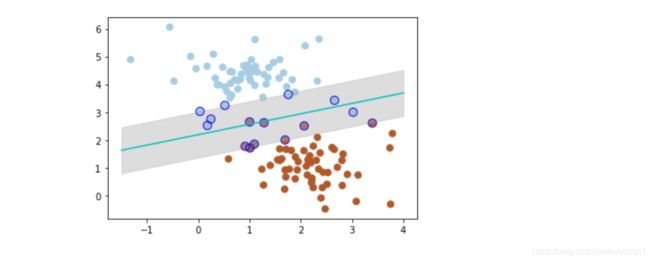
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
            s=80, facecolors='none')

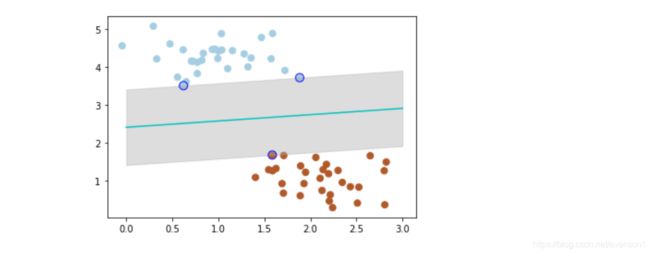
带黑边的点是距离当前分类器最近的点，我们称之为支持向量。
支持向量机为我们提供了在众多可能的分类器之间进行选择的原则，从而确保对未知数据集具有更高的泛化性。

软间隔（个别点混在间隔带中）

# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)

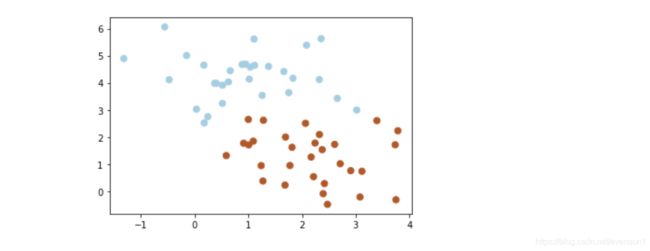
如果没有一个原则进行约束，满足软间隔的分类器也会出现很多条。
所以需要对分错的数据进行惩罚，SVC 函数中，有一个参数 C 就是惩罚参数。
惩罚参数越小，容忍性就越大。

### 以c = 1为例
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 惩罚参数：C=1 
clf = SVC(C=1, kernel='linear')
clf.fit(X, y)

# 最佳函数
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a*x_fit - (clf.intercept_[0]) / w[1]
# 最大边距 下届
b_down = clf.support_vectors_[0]
y_down = a* x_fit + b_down[1] - a * b_down[0]
# 最大边距 上届
b_up = clf.support_vectors_[-1]
y_up = a* x_fit + b_up[1] - a * b_up[0]

# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画函数
plt.plot(x_fit, y_3, '-c')
# 画边距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 画支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
            s=80, facecolors='none')

###惩罚参数 C=0.2 时，SVM 会更具包容性，从而兼容更多的错分样本：
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 惩罚参数：C=0.2 
clf = SVC(C=0.2, kernel='linear')
clf.fit(X, y)

x_fit = np.linspace(-1.5, 4)
# 最佳函数
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a*x_fit - (clf.intercept_[0]) / w[1]
# 最大边距 下届
b_down = clf.support_vectors_[10]
y_down = a* x_fit + b_down[1] - a * b_down[0]
# 最大边距 上届
b_up = clf.support_vectors_[1]
y_up = a* x_fit + b_up[1] - a * b_up[0]

# 画散点图
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 画函数
plt.plot(x_fit, y_3, '-c')
# 画边距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 画支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
            s=80, facecolors='none')

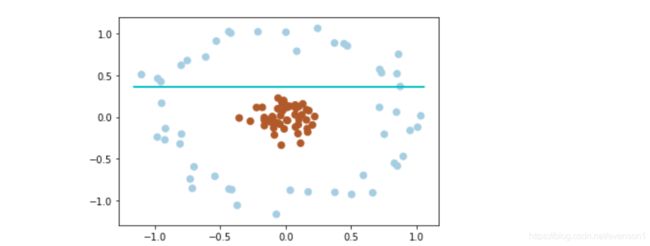
超平面（非线性分类，映射到高维空间）

from sklearn.datasets.samples_generator import make_circles
# 画散点图
X, y = make_circles(100, factor=.1, noise=.1, random_state=2019)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)

clf = SVC(kernel='linear').fit(X, y)

# 最佳函数
x_fit = np.linspace(-1.5, 1.5)
w = clf.coef_[0]
a = -w[0] / w[1]
y_3 = a*X - (clf.intercept_[0]) / w[1]

plt.plot(X, y_3, '-c')

# 数据映射
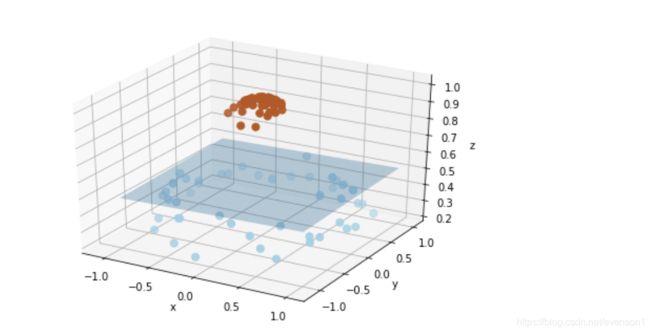
from mpl_toolkits.mplot3d import Axes3D
r = np.exp(-(X[:, 0] ** 2 + X[:, 1] ** 2))

fig = plt.figure()
ax = Axes3D(fig)
ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap=plt.cm.Paired)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

x_1, y_1 = np.meshgrid(np.linspace(-1, 1), np.linspace(-1, 1))
z =  0.01*x_1 + 0.01*y_1 + 0.5
ax.plot_surface(x_1, y_1, z, alpha=0.3)

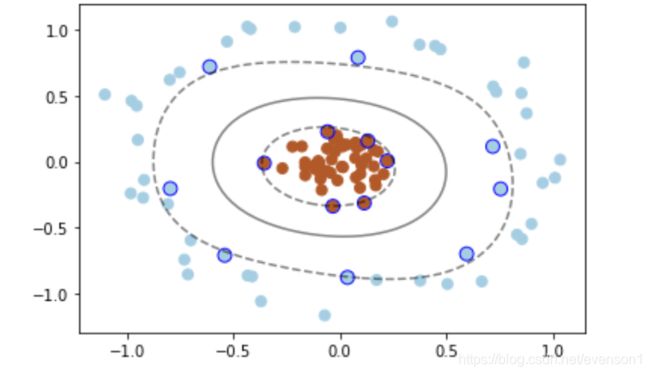
###在 SVC 中可以用高斯核函数来实现这以功能：kernel='rbf'
X, y = make_circles(100, factor=.1, noise=.1, random_state=2019)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
clf = SVC(kernel='rbf')
clf.fit(X, y)


ax = plt.gca()
x = np.linspace(-1, 1)
y = np.linspace(-1, 1)
x_1, y_1 = np.meshgrid(x, y)
P = np.zeros_like(x_1)
for i, xi in enumerate(x):
    for j, yj in enumerate(y):
        P[i, j] = clf.decision_function(np.array([[xi, yj]]))
ax.contour(x_1, y_1, P, colors='k', levels=[-1, 0, 0.9], alpha=0.5,
            linestyles=['--', '-', '--'])

plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
            s=80, facecolors='none');

参考文献

https://zhuanlan.zhihu.com/p/31886934

https://baike.baidu.com/item/%E6%94%AF%E6%8C%81%E5%90%91%E9%87%8F%E6%9C%BA/9683835?fr=aladdin

https://baike.baidu.com/item/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9%98%E6%95%B0%E6%B3%95

https://zhuanlan.zhihu.com/p/77750026?utm_source=wechat_session

https://blog.csdn.net/sinat_20177327/article/details/79729551

https://blog.csdn.net/Dominic_S/article/details/83002153

https://blog.csdn.net/gwb281386172/article/details/102942156