概述
尴尬,学妹问我“冒泡排序、二分查找、希尔排序、快速排序方法”算法的『时间复杂度』,我只能使用百度查询答案进行了回答,但这不符合我的人设,我必须要弄懂这个东西。
作为一个「不称职的攻城狮」,对复杂度的概念是很模糊的,更不要说去计算复杂度了。
但是在开发中对于代码快的执行,做到“提高代码执行率、降低内存占用率”,巧了,这和我百度了解到的『复杂度』相似,然后查询了相关资料,进行一个复习归纳。
简单来说,就是同一个功能:
- 别人写出来运行,内存占用100M,运行时间需要1秒;
- 自己写出来运行,内存占用500M,运行时间需要5秒。
这你能忍?但是在代码开发中是没办法计算内存占用和运行时间情况的,怎么样才能预估代码块达到了较优呢?而且在不同的设备上执行的效果也不同,
比如你新买的手机和用了5年的手机,打开同一个软件所需要的时间肯定是不同的。
但是我们基本的代码块运行次数是可以计算的,这就是我们今天的主角『复杂度』。
PS:衡量不同算法之间的优劣就要用到时间复杂度和空间复杂度。
时间复杂度
什么是时间复杂度?举个例子:
public string attack(int n) { for (int i = 0; i < n; i++) { Console.WriteLine("被攻击"); } return "快来救我"; }
上面代码执行如下:
i = 1 : 执行 1 次 i <= n : 执行 n+1 次 i++ : 执行 n+1 次 Console.WriteLine("被攻击"); : 执行 n 次 return "快来救我" : 执行 1 次
这个方法的总执行次数就是 3n + 4 次,
但是开发过程中不可能都这样去数,所以根据代码执行时间推导过程就有一个规律,这就是所有代码执行时间 T(n)和代码的执行次数 f(n) ,这个是成正比的,而这个规律有一个公式(大欧表示法):
T(n) = O(f(n))
n 是输入数据的大小或者输入数据的数量
T(n) 表示一段代码的总执行时间
f(n) 表示一段代码的总执行次数
O 表示代码的执行时间 T(n) 和 执行次数f(n) 成正比
套用公式可以得到上面方法的复杂度就是:O(3n+4),简化为O(n)。
为什么可以简化为O(n)呢,我们看下简化过程。
- 如果只是常数直接估算为1,O(3) 的时间复杂度就是 O
(1),不是说只执行了1次,而是对常量级时间复杂度的一种表示法。一般情况下,只要算法里没有循环和递归,就算有上万行代码,时间复杂度也是O(1) - O(3n+4) 里常数4对于总执行次数的几乎没有影响,直接忽略不计,系数 3 影响也不大,因为3n和n都是一个量级的,所以作为系数的常数3也估算为1或者可以理解为去掉系数,所以 O(3n+4) 的时间复杂度为 O
(n) - 如果是多项式,只需要保留n的最高次项,O
( 666n³ + 666n² + n ),这个复杂度里面的最高次项是n的3次方。因为随着n的增大,后面的项的增长远远不及n的最高次项大,所以低于这个次项的直接忽略不计,常数也忽略不计,简化后的时间复杂度为 O(n³)
是不是很简单,我们看下常用的时间复杂度。
1、常数阶 O(1)
通过上面的简化过程知道,一般情况下,只要算法里没有循环和递归,就算有上万行代码,时间复杂度也是 O(1),因为它的执行次数不会随着任何一个变量的增大而变长,比如下面这样
public string attack(int n) { int power = 100; int speed = 65; Console.WriteLine("力量是:", power); Console.WriteLine("速度是:", speed); if (power == 200) Console.WriteLine("快来救我"); ..... return "我没事,不用担心"; }
2、线性阶 O(n)
只有一层循环或者递归等,时间复杂度就是 O(n),这样消耗时间随着N变化而变化,比如下面这种
public string attack(int n) { for (int i = 0; i < n; i++) { Console.WriteLine("我没事"); } return "我很好"; } public string runaway(int n) { while(--n>0) Console.WriteLine("跑跑跑"); return "我跑的很快"; } public string gameover(int n) { Console.WriteLine("hhh"); if (--n > 0) { Console.WriteLine(gameover(n)); } return "结束"; }
3、平方阶 O(n²)
就是双重for循环,如果外层的是n,内层的是m,那么复杂度就是O(m*n),比如下面这种
public string attack(int n) { for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { Console.WriteLine("我没事"); } } return "我很好"; }
还记得上面的简化不?这样的,总执行次数为 n + n²,如果是多项式,取最高次项,所以这个时间复杂度也是 O(n²)
public string attack(int n) { for (int i = 0; i < n; i++) { Console.WriteLine("我没事"); } for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { Console.WriteLine("我没事"); } } return "我很好"; }
4、对数阶 O(logN)
下面的循环就按i*2何时=N,就是2的多少次方是N,即log2^N,读作以2为底N的对数。对数公式[1] log不了解的可以点击查看一下,这里不做过多讲解。
int i = 1; while (i < n) i = i * 2;
5、线性对数阶 O(nlogN)
就是for循环套while,如下nlog2^N,读作n倍以2为底N的对数。。对数公式[1] log不了解的可以点击查看一下,这里不做过多讲解。
for (int j = 0; j < n; j++) { int i = 1; while (i < n) i = i * 2; }
6、更多...
其他还有一些时间复杂度的运用,下面由快到慢排列了一下:
| 复杂度 | 名称 |
|---|---|
O(1) |
常数复杂度 |
O(logn) |
对数复杂度 |
O(n) |
线性时间复杂度 |
O(nlogn) |
线性对数复杂度 |
O(n²) |
平方 |
O(n³) |
立方 |
O(2^n) |
指数,一点数据量就卡的不行 |
O(n!) |
阶乘,就更慢了 |
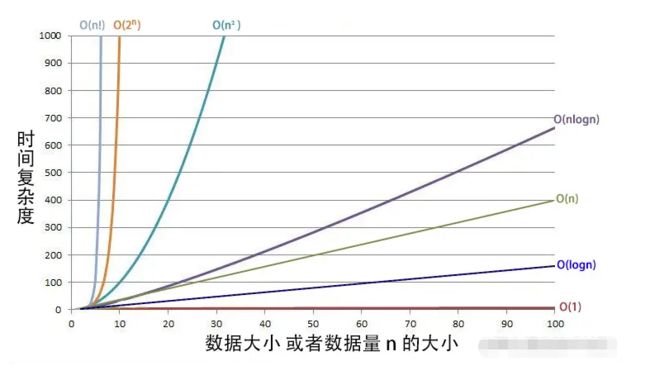
这些时间复杂度有什么区别呢,看张图
随着数据量或者 n 的增大,时间复杂度也随之增加,也就是执行时间的增加,会越来越慢,越来越卡。
总的来说时间复杂度就是执行时间增长的趋势,那么空间复杂度就是存储空间增长的趋势。
空间复杂度
空间复杂度就是算法需要多少内存,占用了多少空间。
常用的空间复杂度有 O(1)、O(n)、O(n²)。
O(1) 就是算法执行临时空间不会随着N发生变化 都算成一个常量,如下。
public string attack(int n) { int j = 0; for (int i = 0; i < n; i++) { j = i; j++; } return "我很好"; }
O(n)就是一开始就开辟的内存,不会在改变,如下new出来了N个,但是N下面循环并没有再开临时变量
public string attack(int n) { int[] m = new int[n]; int j = 0; for (int i = 1; i < n; i++) { j = i; j++; } return "我很好"; }
『空间复杂度』和『时间复杂度』判断标准差不多,主要是看开了多少个临时变量,是否跟N有一定的线性关系。
这都是一些简单的,如果是复杂的怎么计算呢, 下面都计算时间复杂度为例子:
- T(n) = n + 29 一般说是O(n)因为常数项影响函数增长很小
- T(n) = n^3 + n^2 + 29 一般说为O(n3),n3 的增长速度是远超 n^2 的,同时 n^2 的增长速度是远超 n 的,所以有了高次项可以忽略低次项
- T(n) = 3n^3 一般说为O(n^3)因为阶数比乘数影响增长速度最显著我们通常忽略
总结
重新梳理了一遍以后,现在写代码眼里浮现的都是一堆O(1)、O(n)、O(n²)、logN,感觉要疯了。
参考资料
1.百度百科:对数公式
2.如何理解时间复杂度和空间复杂度:https://www.cnblogs.com/magicg/p/15178750.html
3.C#算法的时间复杂度和空间复杂度:https://blog.csdn.net/q_17600689511/article/details/100189543
4.c#算法时间复杂度 面试必看:https://blog.csdn.net/weixin_44370124/article/details/119321322
|
欢迎关注订阅微信公众号【熊泽有话说】,更多好玩易学知识等你来取
作者:熊泽-学习中的苦与乐 公众号:熊泽有话说 出处: https://www.cnblogs.com/xiongze520/p/15666448.html 您可以随意转载、摘录,但请在文章内注明作者和原文链接。
|
![]()