Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference笔记

#1提出问题：如何将复杂的CNNs成功部署到移动端等内存较小的设备中？

【本篇中，中文的中括号里代表的是注释】
解决方案主要分为两类：1.开发新的网络架构【exploit computation or memory efficient operations】【eg：MobileNet SqueezeNet ShuffleNet DenseNet】
2.量化CNN中的权重与激活函数，把原本fp32数据用更低位精度的数据表示。【eg：三元权值网络、二元神经网络】
文中说到，尽管这些网络挺好，但是在权衡延迟和准确性存在两方面不足
乘法运算与位移替换乘法的对比：虽然二进制、三元权值网络能够使用位移实现乘法，只有在操作数很宽的时候，乘法的花销才会显得比较昂贵，在量化之后，位宽降低，避不避免使用乘法就显得没那么重要了。

该文的主要贡献：

1.提出了一种量化方案，量化之后，权重与激活为8位，少部分参数为32位（bias）
2.provide 一个量化的推理框架，能够有效的在整数运算的硬件上实现 ，且描述了在ARM NEON上的高校准确实现
3.为了最大限度地减少量化过程中地信息丢失，设计了一个量化训练框架为量化推理服务。
4.将框架应用于 ARM CPU，基于MobileNets并提供有效的分类和检测系统基准测试结果，在分类、检测【COCO】等方面对 accuracy tradeoffs有显著提升。
该量化方案专注于提高推理速度和精度在移动cpu上的权衡。

本篇paper的量化方案及公式推导：

1.训练的时候用float inference时用int
2.在数学上定义了量化方案，并运用到 int-arithmetic inference & floating-point training 中。
量化的基本要求：只对量化的值使用integer arithmetic [并且需要避免查找表的实现，因为在SIMD硬件系统中，查表的性能相对于pure arithmetic 较差]
【SIMD: SIMD全称Single Instruction Multiple Data，单指令多数据流，能够 复制 多个 操作数 ，并把它们打包在大型 寄存器 的一组 指令集 。】

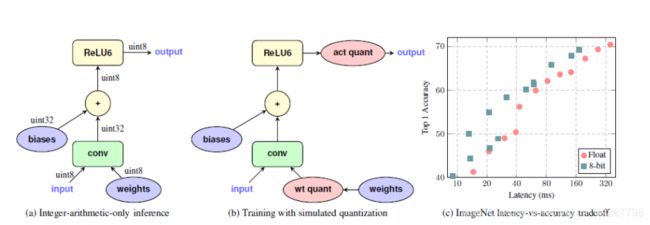
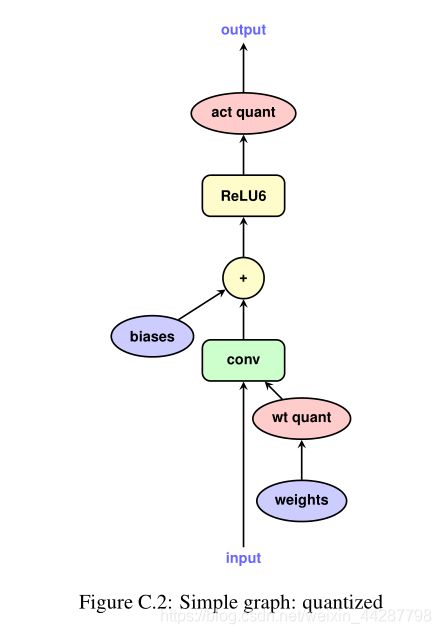
在图a中 input and output都是根据equation 1来的8位int，在卷积环节计算中输入是8位int，输出是32位int，通过累加器与bias结合得到uint8送给ReLU6,最后传给输出。

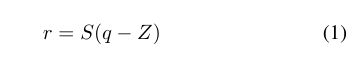
其中 r 是真实值 ， q 是r量化之后的值，S,Z是常数（量化参数）。上面这个方程就是量化方案

并且对于每一个activations array & weight array 的所有值使用一组量化参数，不同的array使用不同的参数。
【确保r=0在量化后仍能被精确表示的前提是在使用padding操作的时候是0填充】

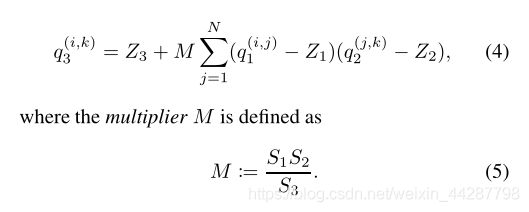
在求出S1、S2、S3之后，虽然M不是int，但是这个数是可以离线完成的，且这个值根据该paper的经验，一直在（0，1）之间。

最后将其表现为这种形式，可以通过提取2^-n次方实现乘法计算

2N^2 = NN + NN(对应每一个i有N次加法)

这个地方为啥两个uint8类型的数值相乘，需要的是一个32位的累加器呢？
主要是由于M虽然是（0，1）之间的数，但是他占的位数却也较高，所以可能就是需要>14位>8位的乘法，再这之后再进行累加，因此16位可能会溢出，只能选用32位，并且ARM/X86系统都是32位的，也就是他们实际情况是想做量化加速，但是硬件设施还是能够支持32位运算的。

对于激活函数，仅仅focus on他的激活功能，在量化方面，还没有融合到这一方面【实际量化过程，倾向于学习利用整个输出【0，255】区间内，因此relu函数此时的功能是钳位】
尽管偏置向量被量化为32位值，但它们只占神经网络参数的很小一部分。此外,使用更高的精度偏差向量 可以满足实际需要:
主要表明bias-vector的重要性，当其量化之后，影响的是整个layer，因此这部分的误差不可忽视。即说明bias虽然量少，但是价值占用的权重比较大。
【这个地方也就意味着我们想把bias量化时，得想办法解决这个问题】

在得到int32累加器的最终值后，还需要做三件事：将值缩小到8位输出激活所使用的最终刻度【或者说将现在的值映射到我们最后那个区间】cast down to uint 8,and应用激活函数得到最后8-bit output activation。
其中 下降比例对应的其实是上面的M，如2.2节所述，它是通过归一化乘子m0和舍入位移位实现的定点乘子。然后，我们执行对uint8的饱和转换，使其饱和到范围[0,255]。

然后 对于激活函数，这个地方是没有融合的，需要做的唯一 一件事就是在存储最终的uint8输出激活之前进一步将uint8值固定在[0,255]的某个子区间上。在实践中，量化训练过程(第3节)倾向于学习利用整个输出uint8[0,255]区间，使激活函数不再做任何事情，

训练量化网络方法：

训练浮点数，然后量化的得到权值【有时需要微调】
对大模型非常有效
【但是对于小模型会导致显著的准确性下降,原因是不同权重的范围差异过大，而前面规定相同层的量化参数是相同的】
#在这个地方，提出了一种在训练前传时 模拟量化效果的方法：反向传播不变，权值和偏置仍然是浮点数易于更新，前向传播传递 通过浮点算法实现量化方案的舍入行为 来模拟量化推理，类似它将在推理引擎中发生的一样，具体如下：
1.权值先量化在送入卷积网络，如果该层有BN，那么BN放在量化前。
2.activation是在inference过程中被量化
更多细节在附录
#量化函数如下

clamp（）函数 如果 r在(a,b)之间，输出的值为r，如果小于a，输出a，大于b，输出b
s（）函数：将(a,b)按位数划分为n个离散的点
q（）函数 ：前面没问题这就没问题了

【权重在[-127,127]内，不取-128，这样提供了大量的优化机会o.o 这一点是对于他们部署的硬件来说的】

附录：

QAT量化流程

一、理解哪部分量化，哪部分不量化
1.简单卷积网络

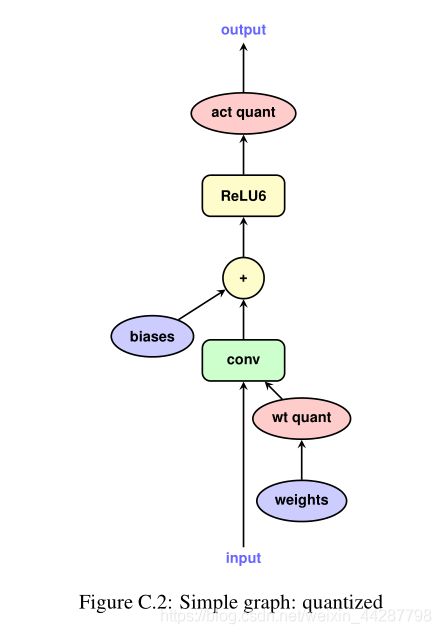
对于一个简单的卷积网络，需要对权重与activation量化，也就是在图中的w后与ReLU函数后加量化环节。在这一篇文章中，biases是没有量化的，第一是biases占的比重较小，二是他们量化只是为了加速，硬件本身是能够支持32浮点运算的强行量化满足不了实际需要。

2.带分支的卷积网络，如resnet

也就是说，在有这种类似跳转的网络连接时，需要在合并之前对输出进行一次量化

3.带BN的网络
如原文3.2所示

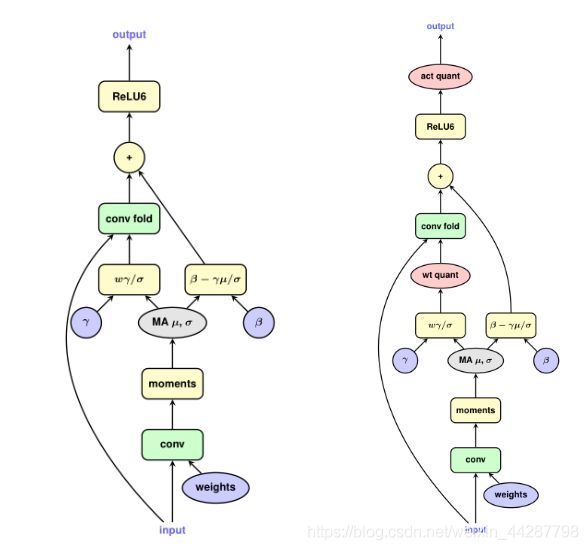
对于使用归一化的模型，为了准确模拟量化结果，我们需要模拟这种fold，并通过批处理归一化参数对权重进行缩放后进行量化。下面是将BNfold到W,B上的原理
1）首先我们看一下卷积最基本的公式以及BN的操作：

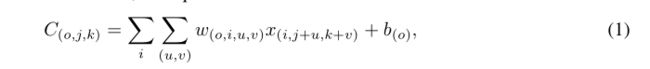
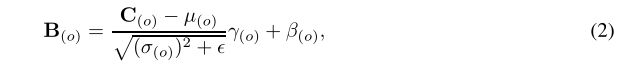
2）然后我们把（1）式代入到（2）式，然后我们就可以把BN融合到W、b中。

可以对比这两张图，就可知在哪个地方添加量化函数了。

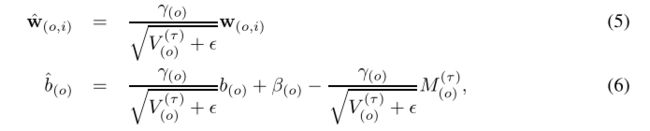
二、如何量化
在这个地方，提出了一种在训练前传时模拟量化效果的方法：反向传播不变，权值和偏置仍然是浮点数以便于更新，前向传播传递 通过浮点算法实现量化方案的舍入行为 来模拟量化推理，类似它将在推理引擎中发生的一样，具体如下：
//这部分看上面的图，更容易理解
1.权值先量化在送入卷积网络，如果该层有BN，那么BN放在量化前。
2.activation是在inference过程中被量化
3.反向推导时，由于量化后的参数是没有梯度的，所以可以根据STE方法进行更新参数，即可以在前向推导时我们使用量化的参数计算，在反向更新时我们采用float更新的方式绕过量化这一个步骤去更新参数，也是俗称的伪量化操作。