简介
有向距离场(signed distance field,SDF)是一张标注了每个像素到最近几何体边缘距离的位图。由于在几何轮廓之外提供了额外的信息,SDF能为二维渲染增加很多灵活性,比如渲染文字时任意调整笔画粗细、放大形状时没有明显锯齿、通过交叉淡化两张SDF来交叉淡化几何轮廓等等。
这里介绍一种通用的有向距离场生成方法:Dead Reckoning(原始文献),它能够从二维位图描述的几何轮廓计算SDF。不同于之前的一些近似算法会得到有“棱角”的结果,Dead Reckoning得出的结果几乎是准确的,接近于全局遍历得到的参考结果。
Dead Reckoning这个名字来源于船舶导航方法,名字中的“dead”可能来源于“deduced”简称之后的语音流变。这种导航方法通过观察一个目标之外的固定标志物来推算与导航目标之间的方位和距离,这与算法中通过观察邻居像素来寻找最近边界有些相似,故而得名。
算法
Dead Reckoning与生物信息学领域的Needleman-Wunsch序列比对算法类似,都是一种动态规划算法。在处理过程中,它不但记录每个像素的边界距离,而且记录对应边界的像素位置,或者说当前的距离是“从哪来的”。
整个计算过程会遍历两遍矩阵,第一次从上向下、从左向右逐行遍历所有像素,第二次反过来从下向上、从右向左。
数据初始化
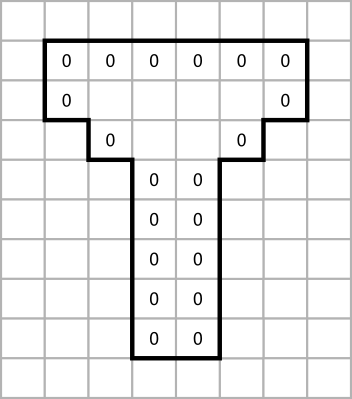
假设输入几何形状存在位图I上,内部像素值为1,外部像素值为0;位图d用来存储距离,位图p用来存储每个像素的最近边界位置的坐标。
位图d:将位于边沿的位置设为零,所有其它位置设为无穷大。
位图p:将位于边沿的位置设为指向自身,所有其它位置设为某个非法值。
这里有个细节问题:如何定义边沿位置。原论文认为应当既包含那些位于几何形状内部的像素,也包含位于外部的像素。也就是说,边界的宽度为2像素。这样的原因是为了数学对称性:将内外部的定义颠倒,对应的SDF也是原SDF求负数。但实际上我们通常并不关心这个对称性,只计入内部的那条边界就可以了。所以边沿的条件是:
I[x,y] == 1 and (
I[x,y]!= I[x-1,y] or
I[x,y]!= I[x+1,y] or
I[x,y]!= I[x,y-1] or
I[x,y]!= I[x,y+1] )两次遍历
遍历每个像素的时候,将它的当前距边界距离与已经处理过的四个邻居比较,如果邻居的当前距边界距离+像素距离比它自己的要小,说明邻居对应的边界更近,就使用邻居的边界信息,并依此更新自己的距离。
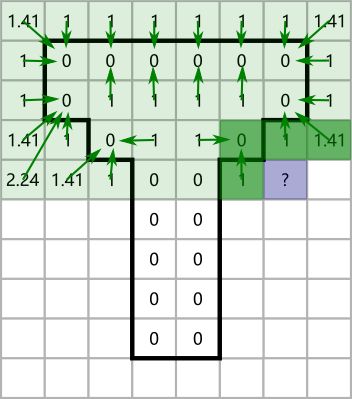
假设左上角是(0,0),那么正向遍历的四个邻居就是它的左、左上、上、右上像素,反向遍历的四个邻居是它的右、右下、下、左下像素。
图中正在进行正向遍历的过程。绿色像素是已经处理过的。蓝色像素是当前要处理的像素,它会从四个相邻的已处理像素(标为深绿色)中获取最近的那个边界位置。
伪代码如下:
// 正向遍历
for y in 1 to height {
for x in 1 to width {
curr_d = d[x,y];
curr_p = p[x,y];
// 检查左上像素
if d[x-1,y-1] + 1.414 < curr_d {
curr_p = p[x-1,y-1];
curr_d = distance((x,y), curr_p);
}
// 检查正上方像素
if d[x,y-1] + 1 < curr_d {
curr_p = p[x,y-1];
curr_d = distance((x,y), curr_p);
}
// 检查右上像素
if d[x+1,y-1] + 1.414 < curr_d {
curr_p = p[x+1,y-1];
curr_d = distance((x,y), curr_p);
}
// 检查正左方像素
if d[x-1,y] + 1 < curr_d {
curr_p = p[x-1,y];
curr_d = distance((x,y), curr_p);
}
d[x,y] = curr_d;
p[x,y] = curr_p;
}
}
// 反向遍历
for y in height to 1 {
for x in width to 1 {
curr_d = d[x,y];
curr_p = p[x,y];
// 检查左下像素
if d[x-1,y+1] + 1.414 < curr_d {
curr_p = p[x-1,y+1];
curr_d = distance((x,y), curr_p);
}
// 检查正下方像素
if d[x,y+1] + 1 < curr_d {
curr_p = p[x,y+1];
curr_d = distance((x,y), curr_p);
}
// 检查右下像素
if d[x+1,y+1] + 1.414 < curr_d {
curr_p = p[x+1,y+1];
curr_d = distance((x,y), curr_p);
}
// 检查正右方像素
if d[x+1,y] + 1 < curr_d {
curr_p = p[x+1,y];
curr_d = distance((x,y), curr_p);
}
d[x,y] = curr_d;
p[x,y] = curr_p;
}
}在正反两次遍历之后,距离d已经填充完成,但是没有区分几何体内外。如果需要这个区分,只需要再遍历依此图像,将位于内部的像素的距离变成负的。
越界处理
当处理位于位图边缘的像素时,逻辑上需要访问不存在的越界像素。不妨令I[越界]为0(外面不属于几何体内部,这很合理),d[越界]为无穷大(于是永远不会指向外面的像素坐标),p[越界]为非法值。
一点思考
Dead Reckoning算法使用每个像素邻居的局部信息替代了全局搜索,为什么仍然可以得到比较准确的结果呢?这可能是因为Voronoi域本身就是比较邻域性的:在引入一些小的位置变化之后,其Voronoi域要么保持不变,就算变化也通常是当前Voronoi域的某个邻居域,几乎不可能跑到完全不相干的老远的一个域上,所以遍历像素的邻居就足够了。
就算几何形状很复杂,但是像素描述的几何形状有精度极限:就是像素大小。那么在同样的精度级别上做遍历处理,大致上依然是足够的。