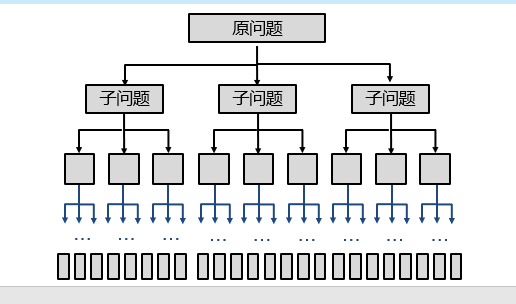
分治思想在归并排序之中可以很好地体现出来。
image.png
归并排序:
下面是程序
java
static public void main(String[] args) throws FileNotFoundException {
//ArrayList
//arrayList.add(1);
//ArrayList list = (ArrayList) arrayList.clone();
//list.add(2);
//System.out.println(arrayList);
//System.out.println(list);
int[] arr = {8,5,3,9,44,2,1,5};
sort(arr);
for (int i = 0; i < arr.length ; i++)
System.out.print(arr[i] + " ");
}
static public void sort(int[] arr){
int[] temp = new int[arr.length];
mysort(arr,0, arr.length-1,temp);
}
static public void mysort(int[] arr,int left, int right,int[] temp){
if(left < right){
int mid = (left + right) / 2;
mysort(arr,left,mid,temp);
mysort(arr,mid+1,right,temp);
merge(arr,left,mid,right,temp);
}
}
//把arr的排序合并之后放在 temp中 再把temp赋值给arr
static public void merge(int[] arr,int left,int mid,int right,int[] temp){
int i = left;
int j = mid + 1;
int t = 0;
while(i<=mid && j <= right){
if (arr[i] >= arr[j]){
temp[t++] = arr[j++];
}else
temp[t++] = arr[i++];
}
//把剩下的赋值给temp
while(i <= mid){
temp[t++] = arr[i++];
}
while(j <= right){
temp[t++] = arr[j++];
}
t = 0;
while(left <= right){
arr[left++] = temp[t++];
}
}
快排
public void quikSort(int[] nums,int begin, int end,int k){ //左闭右开
if (end > begin){
int index = qSort(nums,begin,end);
// if (index == k)
return 0;
quikSort(nums,begin,index-1,k);
quikSort(nums,index+1,end,k);
}
// return 0;
}
public int qSort(int[] nums,int begin, int end){
int value = nums[begin];
while (begin < end) {
while (begin < end && nums[end] >= value)
end--;
if (begin < end)
nums[begin++] = nums[end];
while (begin < end && nums[begin] <= value)
begin++;
if (begin < end)
nums[end--] = nums[begin];
}
nums[begin] = value;
return begin;
}
package dataStruct;
import javax.sql.DataSource;
import javax.xml.crypto.Data;
public class DataStruct {
public static void main(String[] args){
DataStruct dataStruct = new DataStruct();
int[] arr = {3,1,8,5,9,6,2,4};
// dataStruct.insertion_sort(arr,arr.length);
// dataStruct.shellSort(arr,arr.length);
// dataStruct.bubbleSort(arr);
// dataStruct.mergeSort(arr,0,arr.length-1);
dataStruct.heapSort(arr,arr.length);
// dataStruct.quikSort(arr,0,arr.length-1);
// dataStruct.heapSort2(arr,arr.length - 1);
dataStruct.print(arr);
}
public void print(int[] arr){
for (int i = 0; i < arr.length; i++)
System.out.print(arr[i] + " ");
System.out.println(" ");
}
//插入排序
/*
* 先选择从坐标1开始 每选择一个i值 就把0到i值区间排序 我们找到对应的位置 把比target大的值向前移动一个位置 在进行插入
* */
public void insertion_sort(int arr[], int length){
int i,j;
for (i = 1; i < length; i++){
int tmp = arr[i];
for (j = i; j > 0 && tmp < arr[j-1]; j--){
arr[j] = arr[j-1];
}
arr[j] = tmp;
}
}
//希尔排序
/**9
*这个是插入排序的修改版,根据步长由长到短分组,进行排序,直到步长为1为止,属于插入排序的一种。
* 先由步长分组 每一组使用我们的插入排序
*/
public void shellSort(int arr[], int length){
for (int gap = length / 2; gap > 0; gap /= 2){
for (int i = gap; i < length; i++){
int tmp = arr[i];
int j;
for (j = i; j >= gap && arr[j - gap] > tmp; j -= gap){
arr[j] = arr[j-gap];
}
arr[j] = tmp;
}
}
}
//冒泡排序
//相对优雅的冒泡 有一个值来提前判断要不要停止排序
public void bubbleSort(int[] arr) {
boolean swapp = true;
for (int j = 1; j < arr.length; j++) {
swapp = false;
for (int i = 0; i < arr.length - j; i++) {
if (arr[i] > arr[i + 1]) {
arr[i] += arr[i + 1];
arr[i + 1] = arr[i] - arr[i + 1];
arr[i] -= arr[i + 1];
swapp = true;
}
}
if (swapp == false) break;
}
}
//归并排序
/*
*用二分的手法 直接先分后后和
* */
public void mergeSort(int arr[], int l, int r){ //归并也是双闭合
if (r > l){
int mid = l + (r - l) / 2;
mergeSort(arr,l,mid);
mergeSort(arr,mid+1,r);
merge(arr,l,mid,r);
}
}
public void merge(int[] arr,int l, int mid,int r){ // l ~ mid mid+1 ~ r
int i = 0;
int j = 0;
int n1 = mid - l + 1; //先拿到n1 的数量
int n2 = r - mid; //先分别取两数组长度
int[] left = new int[n1];
int[] right = new int[n2];
for (int x = 0; x < left.length; x++)
left[x] = arr[x + l];
for (int x = 0; x < right.length; x++)
right[x] = arr[x + mid + 1];
int t = l;
while (i < left.length && j < right.length){
if (left[i] < right[j])
arr[t++] = left[i++];
else
arr[t++] = right[j++];
}
while (i < left.length)
arr[t++] = left[i++];
while (j < right.length)
arr[t++] = right[j++];
}
public void swap(int[] nums, int index1, int index2){
int tmp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = tmp;
}
//堆排序 最大堆的最大元素在根节点 堆中每个父节点比子节点大
/**
* 这里我们的堆排序的起始点从 0 开始 所以他的左子节点的序号是 2 * i +1 右结点的序号是 2 * i + 2
* 如果从起始点从1 开始的话 我们的左子节点为 2 * i 右节点为 2 * 1;
*
*/
public void heapify(int arr[], int len, int index){ //index 代表 parent 建立堆 不符合递归调用
int value = arr[index];
for (int j = 2 * index + 1; j < len; j = j * 2 + 1){
if (j < len -1 && arr[j] < arr[j + 1]) j++; //比较左右结点大小 找出最大的
if (value > arr[j]) break;
arr[index] = arr[j];
index = j; //记录下来 value 应该放置的位置
}
arr[index] = value;
}
public void heapSort(int arr[], int n) {
// 建立堆
for (int i = arr.length / 2 - 1 ; i >= 0; i--) //调整为堆
heapify(arr, arr.length, i);
// 一个个从堆顶取出元素
for (int i = arr.length-1; i>= 0; i--)
{
System.out.print(arr[0] + " ");
swap(arr,0,i); //取
heapify(arr, i, 0); //取完之后需要重建堆
}
System.out.println("\n");
}
//起始结点从 1 开始 len为数组长度
public void heapify2(int arr[], int len, int index) {
int largestIndex = index;
int left = 2 * index;
int right = 2 * index + 1;
if (len >= left && arr[left] > arr[largestIndex]) {
largestIndex = left;
}
if (len >= right && arr[right] > arr[largestIndex])
largestIndex = right;
if (index != largestIndex) {
swap(arr, largestIndex, index);
heapify2(arr, len, largestIndex);
}
}
//注意边界条件 从0 开始是 n /2 1 开始是n / 2 - 1 这是从1 开始
public void heapSort2(int[] arr , int len){
for (int i = len / 2 ; i >= 1; i--)
heapify2(arr,len,i);
//取堆顶
for (int i = len; i >= 1; i--){
System.out.print(arr[1] +" ");
swap(arr,1,i);
heapify2(arr,i-1,1);
}
System.out.println("\n");
}
public void quikSort(int[] nums,int begin, int end){ //左闭右闭 快排必须双闭合
if (end > begin){
int index = qSort(nums,begin,end);
quikSort(nums,begin,index-1);
quikSort(nums,index+1,end);
}
}
public int qSort(int[] nums,int begin, int end){
int value = nums[begin];
while (begin < end) {
while (begin < end && nums[end] >= value)
end--;
if (begin < end)
nums[begin++] = nums[end];
while (begin < end && nums[begin] <= value)
begin++;
if (begin < end)
nums[end--] = nums[begin];
}
nums[begin] = value;
return begin;
}
}