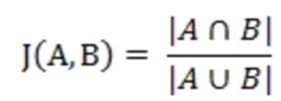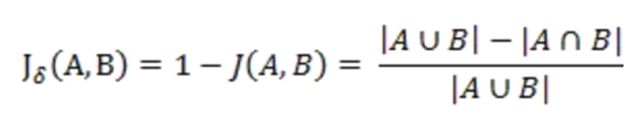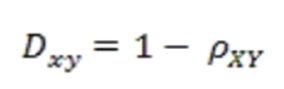【万字详解·附代码】机器学习分类算法之K近邻(KNN)
目录
什么是K近邻算法?
关于空间的一些基本概念
几何空间的五条公理
向量
关于距离的一些基本概念
欧氏距离(Euclidean distance)
曼哈顿距离(Manhattan Distance)
切比雪夫距离 (Chebyshev Distance)
闵可夫斯基距离(Minkowski Distance)
杰卡德距离(Jaccard Distance)
余弦距离(Cosine Distance)
相关距离(Correlation distance)
汉明距离(Hamming Distance)
关于距离的总结
物理几何空间距离(欧氏距离为代表)
欧氏距离和余弦距离的差异
欧氏距离和余弦距离的差异
基于概率统计的距离
KNN算法原理
KNN算法代码实现
参数说明
KNN例子代码
ROC曲线和AUC
每文一语
k-NN 算法最简单的版本只考虑一个最近邻,也就是与我们想要预测的数据点最近的训练,数据点。预测结果就是这个训练数据点的已知输出。
什么是K近邻算法?
KNN的全称是K Nearest Neighbors,意思是K个最近的邻居,从这个名字我们就能看出一些KNN算法的蛛丝马迹了。K个最近邻居,毫无疑问,K的取值肯定是至关重要的。那么最近的邻居又是怎么回事呢?其实啊,KNN的原理就是当预测一个新的值x的时候,根据它距离最近的K个点是什么类别来判断x属于哪个类别。
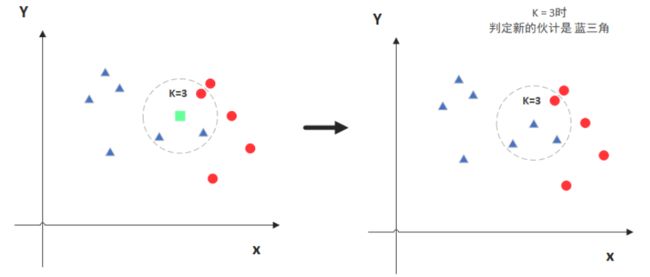
简单来说就是根据“距离”进行判别,看一下下面的示例图,也许你就懂了。
图中绿色的点就是我们要预测的那个点,假设K=3。那么KNN算法就会找到与它距离最近的三个点(这里用圆圈把它圈起来了),看看哪种类别多一些,比如这个例子中是蓝色三角形多一些,新来的绿色点就归类到蓝三角了
在介绍KNN算法的原理前,首先先介绍一些基本的概念
关于空间的一些基本概念
几何空间的五条公理
1.从一点向另一点可以引一条直线。
2.任意线段能无限延伸成一条直线。
3.给定任意线段,可以以其一个端点作为圆心,该线段作为半径作一个圆。
4.所有直角都相等。
5.若两条直线都与第三条直线相交,并且在同一边的内角之和小于两个直角,则这两条直线在这一边必定相交
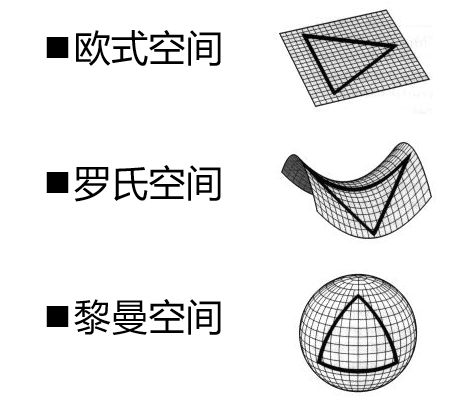
向量空间又分为下面三种:
维度
向量
空间中具有大小和方向的量叫做空间向量
我们可以想象我们我们所分析的数据的每一个属性视为一个向量维度,我们输入的数据其实是某个高维向量空间中的一个点
关于距离的一些基本概念
很多基于向量空间的分类器在分类决策时用到距离的概念。
1、欧氏距离(Euclidean distance)
2、曼哈顿距离(Manhattan Distance)
3、切比雪夫距离 (Chebyshev Distance)
4、闵可夫斯基距离(Minkowski Distance)
5、杰卡德距离(Jaccard Distance)
6、余弦距离(Cosine Distance)
7、相关距离(Correlation distance)
8、汉明距离(Hamming Distance)
欧氏距离(Euclidean distance)
两个点在空间中的最短直线距离
曼哈顿距离(Manhattan Distance)
又称 “城市街区距离”(City Block distance)或“出租车距离”,指从一个十字路口开车到另一个十字路口的驾驶距离,显然不是两点间直线距离。
(1) 二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离:
(2) n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的曼哈顿距离:
切比雪夫距离 (Chebyshev Distance)
国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。
闵可夫斯基距离(Minkowski Distance)
闵氏距离不是一种距离,而是一组距离的定义,是对多个距离度量公式的概括性的表述。
两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为:
其中p是一个变参数:
当p=1时,就是曼哈顿距离;
当p=2时,就是欧氏距离;
当p→∞时,就是切比雪夫距离。
杰卡德距离(Jaccard Distance)
杰卡德相似系数(Jaccard similarity coefficient):两个集合A和B的交集元素在A,B的并集中所占的比例,称为两个集合的杰卡德相似系数,用符号J(A,B)表示:
杰卡德距离(Jaccard Distance):与杰卡德相似系数相反,用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度:
杰卡德相似系数和杰卡德距离的用途
可将杰卡德相似系数用在衡量样本的相似度上。
假设:样本A与样本B是两个n维向量,而且所有维度的取值都是0或1。例如:A(0111)和B(1011)。我们将样本看成是一个集合,1表示集合包含该元素,0表示集合不包含该元素。那么样本A与B的杰卡德相似系数可以表示为:
杰卡德距离等于1-J
说明:
P:样本A与B都是1的维度的个数
q:样本A是1,样本B是0的维度的个数
r:样本A是0,样本B是1的维度的个数
s:样本A与B都是0的维度的个数
余弦距离(Cosine Distance)
余弦距离又称余弦夹角,在几何中可用来衡量两个向量方向的差异。机器学习中,借用这一概念来衡量样本向量之间的差异。
(1)二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式:
(2)两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦为:
余弦距离的意义
余弦夹角取值范围为[-1,1]。余弦越大表示两个向量的夹角越小,余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值1,当两个向量的方向完全相反余弦取最小值-1。
相关距离(Correlation distance)
相关系数:是衡量随机变量X与Y相关程度的一种方法,相关系数的取值范围是[-1,1]。相关系数的绝对值越大,则表明X与Y相关度越高。当X与Y线性相关时,相关系数取值为1(正线性相关)或-1(负线性相关):
相关距离:
汉明距离(Hamming Distance)
定义:两个等长字符串s1与s2的汉明距离为:将其中一个变为另外一个所需要作的最小字符替换次数。
汉明重量:是字符串相对于同样长度的零字符串的汉明距离,也就是说,它是字符串中非零的元素个数:对于二进制字符串来说,就是 1 的个数,所以 11101 的汉明重量是 4。因此,如果向量空间中的元素a和b之间的汉明距离等于它们汉明重量的差a-b。
应用场景:汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。比如在信息编码过程中,为了增强容错性,应使得编码间的最小汉明距离尽可能大。但是,如果要比较两个不同长度的字符串,不仅要进行替换,而且要进行插入与删除的运算,在这种场合下,通常使用更加复杂的编辑距离等算法。
关于距离的总结
物理几何空间距离(欧氏距离为代表)
优点:
容易理解,计算简单,而且在样本各个维度数据完整好的情况下具有较理想的预判效果。
缺陷:
1)将各个分量的量纲(scale),也就是“单位”相同的看待了;
2)未考虑各个分量的分布(期望,方差等)可能是不同的。
替代:马氏距离(Mahalanobis Distance),一种基于样本分布的距离。物理上就是在规范化的主成分空间中的欧氏距离。所谓规范化的主成分空间就是已经利用主成分分析对一些数据进行了主成分分解,并且对所有主成分分解轴做了归一化,形成新坐标轴。这些新坐标轴组成的空间就是规范化的主成分空间。
欧氏距离和余弦距离的差异
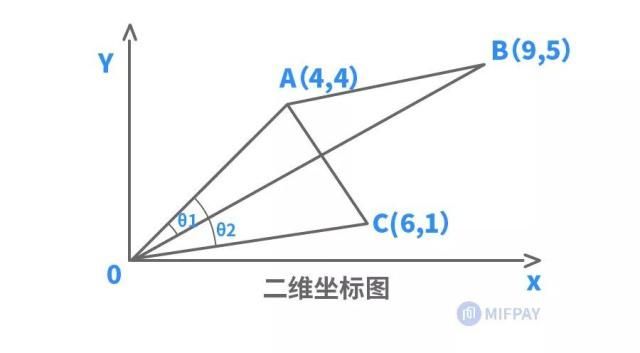
举例:左下图两个等边三角形,已知边长坐标,求两者之间距离。
可以发现,欧式距离跟余弦距离判断结果恰好相反。
欧氏距离和余弦距离的差异
原因:
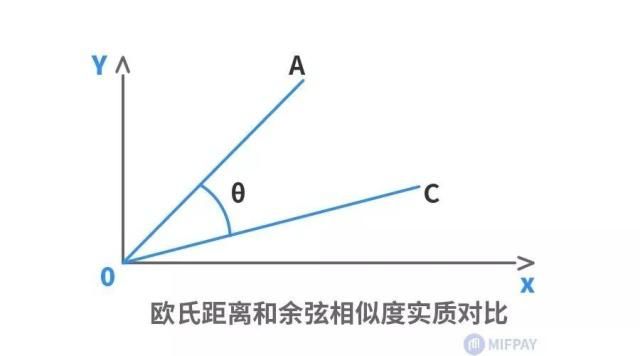
欧氏距离和余弦相似度各自的计算方式和衡量角度不相同,欧氏距离关注的是两点之间的绝对距离,而夹角余弦相似度注重的是两个向量在方向上的差异,而非距离。
如下二维坐标图中,有A、C两个样本,欧氏距离关注的是AC两点的直线段距离,与OA、OC线段长度密切相关;而夹角余弦则是关注OA线段与OC线段重合需扫过的角度(θ)大小,与OA、OC线段长度无关。因此,夹角余弦相似度是整体方向性上的判断,而欧氏距离则是各分量特征的绝对差值判断。
基于概率统计的距离
如需考虑分量相关性、个体相对于总体的比重等相关因素,更多则是采用基于概率统计的分布距离,较常用的有:马氏距离、巴氏距离、杰卡德相似系数、皮尔逊相关系数等。这些距离的计算多涉及统计学及概率论知识,因而相对较复杂。
KNN算法原理
为了判定未知样本的类别,以全部训练样本作为代表点,计算未知样本与所有训练样本的距离,并以最近邻者的类别作为决策未知样本类别的唯一依据。
KNN分类器是对NN算法的一种改进
算法步骤:
1)计算待分类点与已知类别的点之间的距离
2)按照距离递增次序排序
3)选取与待分类点距离最小的k个点
4)确定前k个点所在类别的出现次数
5)返回前k个点出现次数最高的类别作为待分类点的预测分类
举例说明
如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那类
如果K=5,蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。
KNN算法需要确定K值、距离度量和分类决策规则
K值过小时,只有少量的训练样本对预测起作用,容易发生过拟合,或者受含噪声训练数据的干扰导致错误
K值过大,过多的训练样本对预测起作用,当不同类别样本数量不均衡时,结果偏向数量占优的样本
距离度量在KNN中,通过计算对象间距离来作为各个对象之间的相似性指标,距离一般使用欧氏距离或曼哈顿距离:
优点:
1、容易理解,实现简单
2、只需保存训练样本和标记,无需估计参数和训练
3、不易受最小错误概率的影响。理论证明,最近邻的渐进错误率最坏不超过两倍的贝叶斯错误率,最好则接近或达到贝叶斯错误率。
缺点:
1、K值选择不固定,且对分类结果有较大影响。
2、预测结果容易受噪声数据影响。
3、样本不均衡时,新样本的预测会偏向数量占优的一方
4、具有较高的计算复杂度和内存消耗量
KNN算法代码实现
参数说明
class sklearn.neighbors.KNeighborsClassifier(
n_neighbors=5,
weights=’uniform’,
algorithm=’auto’,
leaf_size=30,
p=2,
metric=’minkowski’,
metric_params=None,
n_jobs=None,
**kwargs)| 参数名 |
类型 |
是否必填 |
默认值 |
说明 |
| n_neighbors |
int |
N |
5 |
用于[kneighbors]查询的默认邻居的数量 |
| weights |
str callable |
N |
uniform |
用于预测的权重函数。可选参数如下: - ‘uniform’ : 统一的权重. 在每一个邻居区域里的点的权重都是一样的。 - ‘distance’ : 权重点等于他们距离的倒数。使用此函数,更近的邻居对于所预测的点的影响更大。 - [callable] : 一个用户自定义的方法,此方法接收一个距离的数组,然后返回一个相同形状并且包含权重的数组 |
| algorithm |
string |
N |
auto |
计算最近邻居用的算法: - ‘ball_tree’ 使用算法[BallTree] - ‘kd_tree’ 使用算法[KDTree] - ‘brute’ 使用暴力搜索. - ‘auto’ 会基于传入[fit]方法的内容,选择最合适的算法。 注意 : 如果传入fit方法的输入是稀疏的,将会重载参数设置,直接使用暴力搜索。 |
| 参数名 |
类型 |
是否必填 |
默认值 |
说明 |
| leaf_size |
int |
N |
30 |
传入BallTree或者KDTree算法的叶子数量。此参数会影响构建、查询BallTree或者KDTree的速度,以及存储BallTree或者KDTree所需要的内存大小。 此可选参数根据是否是问题所需选择性使用。 |
| p |
int |
N |
5 |
用于Minkowski metric的超参数。 p = 1, 相当于使用[曼哈顿距离] p = 2, 相当于使用[欧几里得距离] 对于任何 p ,DistanceMetric这个类文档 |
| metric_params |
dict |
N |
None |
给矩阵方法使用的其他的关键词参数 |
| metric |
string callable |
N |
minkowski |
用于树的距离矩阵。默认为[闵可夫斯基空间],如果和p=2相当于使用标准欧几里得矩阵. 所有可用的矩阵列表请查询 DistanceMetric 的文档 |
| n_jobs |
int |
N |
1 |
用于搜索邻居的,可并行运行的任务数量。如果为-1, 任务数量设置为CPU核的数量。不会影响[fit]方法。 |
话不多说,开始上代码
KNN例子代码
导入第三方库
#导入所需要的包
from sklearn.metrics import precision_score
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import classification_report
from sklearn.model_selection import GridSearchCV #网格搜索初次加载模型和训练(无任何模型参数)
# 加载模型
model = KNeighborsClassifier()
# 训练模型
model.fit(X_train,y_train)
# 预测值
y_pred = model.predict(X_test)
'''
评估指标
'''
# 求出预测和真实一样的数目
true = np.sum(y_pred == y_test )
print('预测对的结果数目为:', true)
print('预测错的的结果数目为:', y_test.shape[0]-true)
# 评估指标
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,cohen_kappa_score
print('预测数据的准确率为: {:.4}%'.format(accuracy_score(y_test,y_pred)*100))
print('预测数据的精确率为:{:.4}%'.format(
precision_score(y_test,y_pred)*100))
print('预测数据的召回率为:{:.4}%'.format(
recall_score(y_test,y_pred)*100))
# print("训练数据的F1值为:", f1score_train)
print('预测数据的F1值为:',
f1_score(y_test,y_pred))
print('预测数据的Cohen’s Kappa系数为:',
cohen_kappa_score(y_test,y_pred))
# 打印分类报告
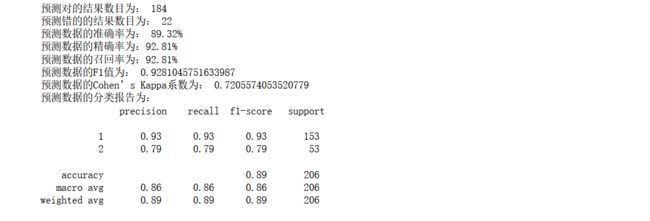
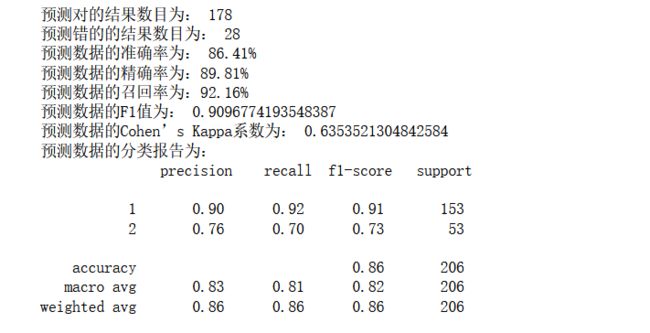
print('预测数据的分类报告为:','\n',
classification_report(y_test,y_pred))效果一般般,下面进行一个初次的重要参数,寻找
寻找最佳的邻居数
training_accuracy = []
test_accuracy = []
# n_neighbors取值从1到10
neighbors_settings = range(1, 11)
for n_neighbors in neighbors_settings:
# 构建模型
clf = KNeighborsClassifier(n_neighbors=n_neighbors)
clf.fit(X_train, y_train)
# 记录训练集精度
training_accuracy.append(clf.score(X_train, y_train))
# 记录泛化精度
test_accuracy.append(clf.score(X_test, y_test))
plt.plot(neighbors_settings, training_accuracy, label="training accuracy")
plt.plot(neighbors_settings, test_accuracy, label="test accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.legend() 通过可视化分析得知,在n_neighbors取到:4,7,8,效果还可以,但是推荐使用5,因为综合训练集和测试集,还是不错的
参数调优
这里提前使用一个网格搜索的知识,后面更新完所有的模型,将会详细的用一篇文章来讲解模型如何调优,其中就有网格搜索
这里根据已有的参数进行迭代,最后返回最佳的参数
#超参数配置
param_knn = {
'n_neighbors': list(range(3,15,2)),
'algorithm':['auto', 'ball_tree', 'kd_tree', 'brute'],
'metric':['euclidean','manhattan','chebyshev','minkowski'],
'p':list(range(1,6)),
'weights':['distance','uniform']
}
#KNN的超参数
gsearch_knn = GridSearchCV( model , param_grid = param_knn, cv=10 )
gsearch_knn.fit( X_train, y_train )
gsearch_knn.best_params_
gsearch_knn.best_score_
best_knn=gsearch_knn.best_estimator_
#训练模型+预测数据
y_pred = best_knn.predict(X_test)第二次训练和评估
'''
评估指标
'''
# 求出预测和真实一样的数目
true = np.sum(y_pred == y_test )
print('预测对的结果数目为:', true)
print('预测错的的结果数目为:', y_test.shape[0]-true)
# 评估指标
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,cohen_kappa_score
print('预测数据的准确率为: {:.4}%'.format(accuracy_score(y_test,y_pred)*100))
print('预测数据的精确率为:{:.4}%'.format(
precision_score(y_test,y_pred)*100))
print('预测数据的召回率为:{:.4}%'.format(
recall_score(y_test,y_pred)*100))
# print("训练数据的F1值为:", f1score_train)
print('预测数据的F1值为:',
f1_score(y_test,y_pred))
print('预测数据的Cohen’s Kappa系数为:',
cohen_kappa_score(y_test,y_pred))
# 打印分类报告
print('预测数据的分类报告为:','\n',
classification_report(y_test,y_pred))发现效果明显的有所提升!
最优参数:
然后将这些最佳参数添加到模型,将一些自定义的模型参数也添加进去,看看效果如何:
# 加载模型
model = KNeighborsClassifier(n_neighbors=7,algorithm='ball_tree',metric='manhattan',p=1,weights='distance')
# 训练模型
model.fit(X_train,y_train)
# 预测值
y_pred = model.predict(X_test)
'''
评估指标
'''
# 求出预测和真实一样的数目
true = np.sum(y_pred == y_test )
print('预测对的结果数目为:', true)
print('预测错的的结果数目为:', y_test.shape[0]-true)
# 评估指标
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,cohen_kappa_score
print('预测数据的准确率为: {:.4}%'.format(accuracy_score(y_test,y_pred)*100))
print('预测数据的精确率为:{:.4}%'.format(
precision_score(y_test,y_pred)*100))
print('预测数据的召回率为:{:.4}%'.format(
recall_score(y_test,y_pred)*100))
# print("训练数据的F1值为:", f1score_train)
print('预测数据的F1值为:',
f1_score(y_test,y_pred))
print('预测数据的Cohen’s Kappa系数为:',
cohen_kappa_score(y_test,y_pred))
# 打印分类报告
print('预测数据的分类报告为:','\n',
classification_report(y_test,y_pred))效果非常棒!
ROC曲线和AUC
from sklearn.metrics import precision_recall_curve
from sklearn import metrics
# 预测正例的概率
y_pred_prob=model.predict_proba(X_test)[:,1]
# y_pred_prob ,返回两列,第一列代表类别0,第二列代表类别1的概率
#https://blog.csdn.net/dream6104/article/details/89218239
fpr, tpr, thresholds = metrics.roc_curve(y_test,y_pred_prob, pos_label=2)
#pos_label,代表真阳性标签,就是说是分类里面的好的标签,这个要看你的特征目标标签是0,1,还是1,2
roc_auc = metrics.auc(fpr, tpr) #auc为Roc曲线下的面积
# print(roc_auc)
plt.figure(figsize=(8,6))
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.plot(fpr, tpr, 'r',label='AUC = %0.2f'% roc_auc)
plt.legend(loc='lower right')
# plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([0, 1.1])
plt.ylim([0, 1.1])
plt.xlabel('False Positive Rate') #横坐标是fpr
plt.ylabel('True Positive Rate') #纵坐标是tpr
plt.title('Receiver operating characteristic example')
plt.show()这个时候,发现模型的效果已经可以了,自我感觉还是不错的,但是在基于上一篇文章,贝叶斯模型,我们使用了特征筛选的方法,来提高模型的效果,这里是不是也可以了。
我通过了一些树模型进行筛选出最佳的14个特征,发现效果并没有全部放入模型的效果好
筛选出最佳的特征如上
发现效果没有上面那一个好,这是为什么呢,可能这里和KNN的算法原理有关,这里特征通过专家的验证,并不是毫无相关的特征,所以KNN的联合特征算法在这里得到了验证,一般过特征的选取来提高模型的效果是基于不同的模型
每文一语
新的一年开始啦,希望不负青春!