论文阅读 || 深度学习之空洞卷积

论文地址：Multi-scale context aggregation with dilated convolutions

空洞卷积（Dilated/Atrous Convolution），就是在标准的卷积里面注入空洞，以此来增加感受野的大小。

1 原理的介绍

1.1 空洞卷积的引入

Deep CNN对于某些任务有致命的缺陷。较为明显的为pooling layer (优点：减小特征图尺寸、增大感受野) 和 up-sampling。表现为：

• maxpooling导致分辨率下降、局部信息丢失
• 小物体信息无法重建（假设有四个pooling layer，则任何小于16pixel的物体信息将理论上无法重建）

在图像分割领域，图像输入到CNN（典型的网络比如FCN[3]）中，FCN先像传统的CNN一样对图像做出卷积在pooling，降低图像尺寸的同时增大感受野。但由于图像分割预测是pixel-wise的输出，所以要将pooling后较小的图像尺寸upsampling到原始的图像尺寸进行预测。
故FCN中有两个关键：一个是pooling减小图像尺寸增大感受野，另一个是upsampling扩大图像尺寸。这个过程中，必然有一些信息丢失。于是就设计一种新的操作，不通过pooling也能有较大的感受野——dilated conv。

• 1.2 空洞卷积的好处

不改变特征图的尺寸，不增加参数，加大感受野。

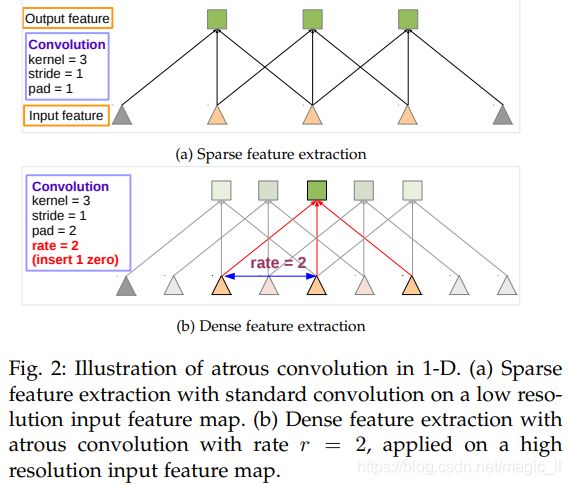
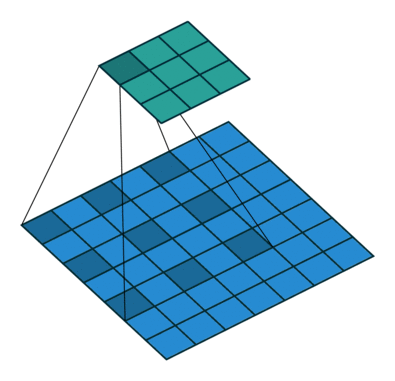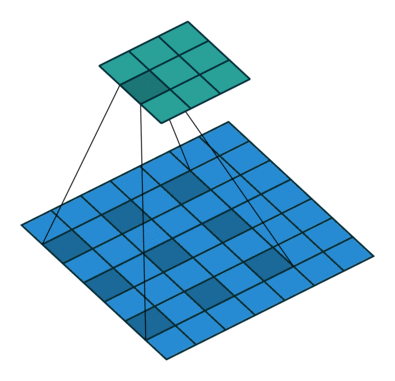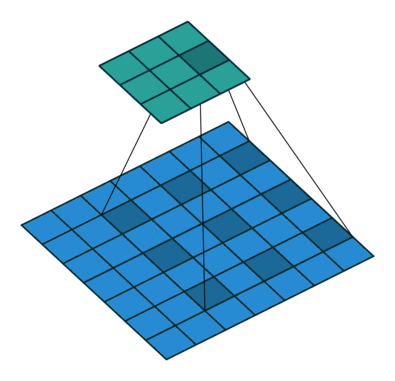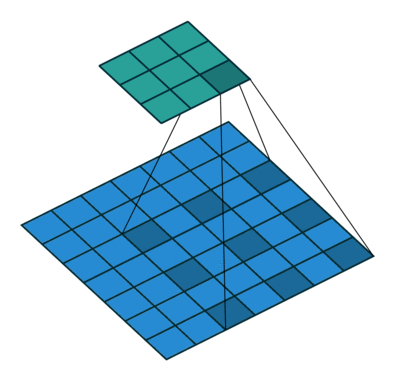
(a)图对应的3x3的1-dilated conv，和普通的卷积操作一样
(b)图对应的3x3的2-dilated conv，实际的卷积kernel size还是3x3。但空洞为1，也就是对于对于一个7x7的图像patch，只有9个红色的点和3x3的kernel发生卷积操作，其余点略过。也可以理解为7x7的kernel，但只有图中9个点的权重不为0，其余都为0。
  此时，虽然kernel size只有3x3，但是这个卷积的感受野已经增大到了7x7（感受野内不是所有数据都处理，比如边界的像素值）。（假设这个2-dilated的前一层是一个dilated conv的话，那么每个红点就是1-dilated的卷积的输出，所以感受野为3x3。这样1-dilated和2-dilated合起来就能达到7x7的conv）
(c)图是4-dilated conv操作，同理跟在两个1-dilated和2-dilated conv的后面，能达到15x15的感受野。对比传统的conv操作，3层3x3的卷积加起来，stride为1的话，只能达到 (kernel-1)*layer+1=7的感受野。也就是和层数layer成线性关系，而dilated conv的感受野是指数级的增长。

1.3 空洞卷积的相关计算

(参考于deeplabv2)首先考虑一维信号。空洞卷积的输出为，输入为，size为K的滤波器，rate=r。定义为

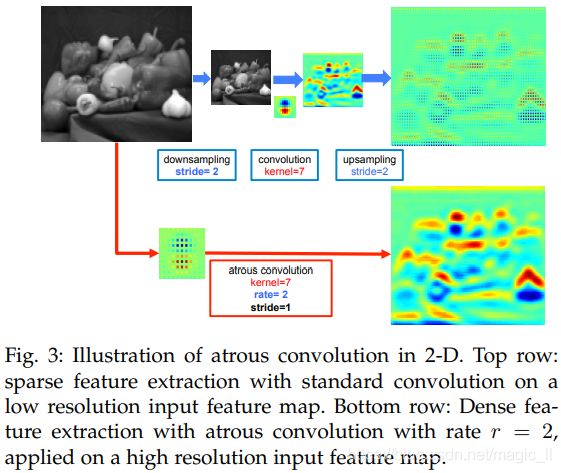
使用上面两种空洞卷积，在二维信号（图片）上使用空洞卷积的表现

• 上分支：【下采样1/2】 -- 【卷积】--【上采样2倍】。本质上这只是在愿图片上的1/4内容上做了卷积响应
• 下分支：【使用rate=2的空洞卷积】。这种方式得到了整张图像的响应，效果更佳
• 两种操作的卷积，具有相同的参数和感受野，但效果后者更佳。

空洞卷积可以增大感受野。rate=r 会引入 r-1 个零，有效的将感受野从【】扩展到【】，而不增加参数和计算量。在CDNN中，常见的做法是混合使用空洞卷积，以高的分辨率（理解为采样密集）计算最终的DCNN网络响应。

 

2. 空洞卷积存在的问题

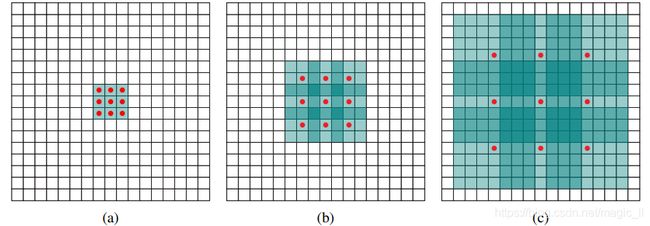
潜在问题1：the gridding effect

假设我们仅仅多次叠加dilation rate 2的3x3 kernel 的话，则会出现这个问题：

会发现我们的kernel并不连续，也就是并不是所有的pixel都参与计算，因此这里将信息看做 checker-board的方式会损失信息的连续性。这对pixel-level dense prediction 的任务来说是致命的

潜在问题2：Long-ranged information might be not relevant

我们从dilated convolution的设计背景来看就能推测出这样的设计是用来获取long-ranged information。然而只采用dilation rate的信息或许只对一下大物体分割有效果，二队小物体来说则有弊无利了。如何同时处理不同大小物体的关系，则是设计好 dilated convolution网络结构的关键。

3 Hybrid Dilated Convolution (HDC)的设计

对于上面提出的问题，提出了相应的解决方法：

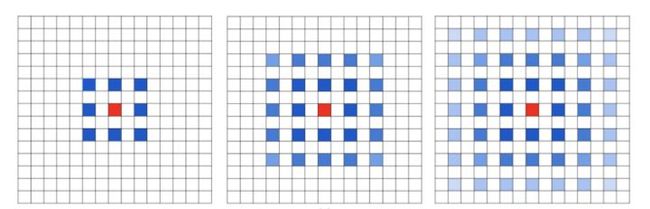
• 第一个特性：叠加卷积的dilation rate 不能有大于1的公约数。比如[2, 4, 6]则不是一个号的三层卷积，依然会出现gridding effect
• 第二个特性：我们将dilation rate 设计成锯齿状结构，例如 [1, 2, 5, 1, 2, 5]循环结构。

一个较为常用的例子：[1,2,5] with 3x3 kernel（可行的方案）

而这样的锯齿状本身的性质就比较好的来同时满足小物体大物体的分割要求(小 dilation rate 来关心近距离信息，大 dilation rate 来关心远距离信息)。

个良好设计的 dilated convolution 网络能够有效避免 gridding effect.：

4 多尺度分割的另类解：Atrous Spatial Pyramid Pooling（ASPP）

在处理多尺度分割时，我们通常会有以下几种方式操作：

仅仅在一个卷积分支下，使用dilated convolution 去抓取多尺度物体是一个不正统的方法。比方说，我们用一个HDC的方法来获取一个大（近）车辆的信息，然而对于一个小（远）车辆的信息都不在受用。假设我们再去用小 dilated convolution 的方法重新获取小的车辆信息，就会非常冗余。

ASPP则在网络的decoder上对于不同尺度上用不同大小的dilation rate 来抓取多尺度信息，每个尺度则作为一个独立的分支，在网络最后合并起来，在接一个卷积输出预测label。这样的设计则有效避免了在encoder上冗余的信息的获取，直接关注了物体之间之内的相关性。

5 其他

该种结构，更多的应用在语义分割，其他以及后来的网络结构，也较少的采用空洞卷积。