蓝桥杯第十二届省赛javab

主体是javab组的题目，最下面格外有其它组的题目

试题 A: ASC

本题总分：5 分
【问题描述】
已知大写字母 A 的 ASCII 码为 65，请问大写字母 L 的 ASCII 码是多少？
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

答案：76
题解： 签到，不知道会不会有优秀奖

试题 B: 卡片

本题总分：5 分
【问题描述】
小蓝有很多数字卡片，每张卡片上都是数字 0 到 9。
小蓝准备用这些卡片来拼一些数，他想从 1 开始拼出正整数，每拼一个，
就保存起来，卡片就不能用来拼其它数了。
小蓝想知道自己能从 1 拼到多少。
例如，当小蓝有 30 张卡片，其中 0 到 9 各 3 张，则小蓝可以拼出 1 到 10，
但是拼 11 时卡片 1 已经只有一张了，不够拼出 11。
现在小蓝手里有 0 到 9 的卡片各 2021 张，共 20210 张，请问小蓝可以从 1
拼到多少？
提示：建议使用计算机编程解决问题。
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

答案：3181
题解： 模拟，注意跳出时的值，有人是3180或者3182

试题 C: 直线

本题总分：10 分
【问题描述】
在平面直角坐标系中，两点可以确定一条直线。如果有多点在一条直线上，
那么这些点中任意两点确定的直线是同一条。
给定平面上 2 × 3 个整点 {(x, y)|0 ≤ x < 2, 0 ≤ y < 3, x ∈ Z, y ∈ Z}，即横坐标
是 0 到 1 (包含 0 和 1) 之间的整数、纵坐标是 0 到 2 (包含 0 和 2) 之间的整数
的点。这些点一共确定了 11 条不同的直线。
给定平面上 20 × 21 个整点 {(x, y)|0 ≤ x < 20, 0 ≤ y < 21, x ∈ Z, y ∈ Z}，即横
坐标是 0 到 19 (包含 0 和 19) 之间的整数、纵坐标是 0 到 20 (包含 0 和 20) 之
间的整数的点。请问这些点一共确定了多少条不同的直线。
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

答案：40257
题解： 枚举所有线段，二重循环去重

试题 D: 货物摆放

本题总分：10 分
【问题描述】
小蓝有一个超大的仓库，可以摆放很多货物。
现在，小蓝有 n 箱货物要摆放在仓库，每箱货物都是规则的正方体。小蓝
规定了长、宽、高三个互相垂直的方向，每箱货物的边都必须严格平行于长、
宽、高。
小蓝希望所有的货物最终摆成一个大的立方体。即在长、宽、高的方向上
分别堆 L、W、H 的货物，满足 n = L × W × H。
给定 n，请问有多少种堆放货物的方案满足要求。
例如，当 n = 4 时，有以下 6 种方案：1×1×4、1×2×2、1×4×1、2×1×2、
2 × 2 × 1、4 × 1 × 1。
请问，当 n = 2021041820210418 （注意有 16 位数字）时，总共有多少种
方案？
提示：建议使用计算机编程解决问题。
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

答案：2430
题解： 分解质因数后发现求2021041820210418和270270等价，故三重循环暴力求下n= 270270的个数

试题 E: 路径

本题总分：15 分
【问题描述】
小蓝学习了最短路径之后特别高兴，他定义了一个特别的图，希望找到图
中的最短路径。
小蓝的图由 2021 个结点组成，依次编号 1 至 2021。
对于两个不同的结点 a, b，如果 a 和 b 的差的绝对值大于 21，则两个结点
之间没有边相连；如果 a 和 b 的差的绝对值小于等于 21，则两个点之间有一条
长度为 a 和 b 的最小公倍数的无向边相连。
例如：结点 1 和结点 23 之间没有边相连；结点 3 和结点 24 之间有一条无
向边，长度为 24；结点 15 和结点 25 之间有一条无向边，长度为 75。
请计算，结点 1 和结点 2021 之间的最短路径长度是多少。
提示：建议使用计算机编程解决问题。
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

答案：10266837
题解 最短路径算法+gcd+10秒等待时间

试题 F: 时间显示

时间限制: 1.0s 内存限制: 512.0MB 本题总分：15 分
【问题描述】
小蓝要和朋友合作开发一个时间显示的网站。在服务器上，朋友已经获取
了当前的时间，用一个整数表示，值为从 1970 年 1 月 1 日 00:00:00 到当前时
刻经过的毫秒数。
现在，小蓝要在客户端显示出这个时间。小蓝不用显示出年月日，只需要
显示出时分秒即可，毫秒也不用显示，直接舍去即可。
给定一个用整数表示的时间，请将这个时间对应的时分秒输出。
【输入格式】
输入一行包含一个整数，表示时间。
【输出格式】
输出时分秒表示的当前时间，格式形如 HH:MM:SS，其中 HH 表示时，值
为 0 到 23，MM 表示分，值为 0 到 59，SS 表示秒，值为 0 到 59。时、分、秒
不足两位时补前导 0。
【样例输入 1】
46800999
【样例输出 1】
13:00:00
【样例输入 2】
1618708103123
【样例输出 2】
01:08:23
【评测用例规模与约定】
对于所有评测用例，给定的时间为不超过 1018 的正整数。

题解：取模即可，只要注意不超过24小时和需要用大整数，那么这题就没什么问题了

试题 G: 最少砝码

时间限制: 1.0s 内存限制: 512.0MB 本题总分：20 分
【问题描述】
你有一架天平。现在你要设计一套砝码，使得利用这些砝码可以称出任意
小于等于 N 的正整数重量。
那么这套砝码最少需要包含多少个砝码？
注意砝码可以放在天平两边。
【输入格式】
输入包含一个正整数 N。
【输出格式】
输出一个整数代表答案。
【样例输入】
7
【样例输出】
3
【样例说明】
3 个砝码重量是 1、4、6，可以称出 1 至 7 的所有重量。
1 = 1；
2 = 6 − 4 (天平一边放 6，另一边放 4)；
3 = 4 − 1；
4 = 4；
5 = 6 − 1；
6 = 6；
7 = 1 + 6；
少于 3 个砝码不可能称出 1 至 7 的所有重量。
【评测用例规模与约定】
对于所有评测用例，1 ≤ N ≤ 1000000000。

题解：
1.大部分人用的dp
2.（已证明 正确）
但也有少数人用的找规律，比如笔者我，因为我发现数据规模过大，dp大概率不是唯一方法，当然我的做法过于鲁莽，应该可以同时都写，用dp验证规律的正确性，可惜时间不够，所以目前还不确定正确性，有感兴趣的读者可以帮忙验证一下。

规律如下：
1，3，9，27，81
倍数3的数就是最优的砝码
1,3可以完成1-4
1,3,9可以完成1-13
1,3,9,27,可以完成1-40
1+3+9+27+……+3t>=n
(3^t-1)/2>=n
t的最小值就是答案

推导：
当一个砝码时n最大多少：显然是1
当两个砝码时n最大多少：为了满足称出重量为1，这必定有1砝码或者相邻的两个砝码
发现1，3砝码最大，观察：

1=1
2=3-1
3=3
4=3+1
当三个砝码时n最大多少：
如图：

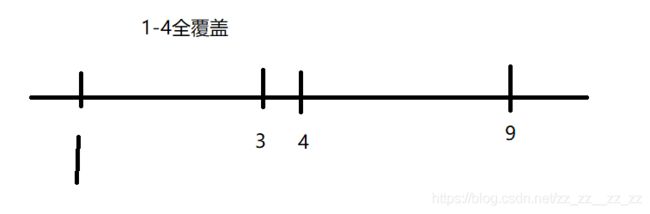
可以发现分治思想
因为2个砝码时1-4全覆盖
那么
5=9-4这里的4为上面的4=3+1
6=9-3
7=9-2这里的2为上面的4=3-1
8=9-1
9=9
故第n个砝码的大小为n=2*(1+3+……3*(n-1))+1
$$即x_n=3x_{n-1}$$
由此可发现之后的砝码是27，81，……

试题 H: 杨辉三角形

时间限制: 5.0s 内存限制: 512.0MB 本题总分：20 分
【问题描述】
下面的图形是著名的杨辉三角形：

如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下
数列：
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, …
给定一个正整数 N，请你输出数列中第一次出现 N 是在第几个数？
【输入格式】
输入一个整数 N。
【输出格式】
输出一个整数代表答案。
【样例输入】
6
【样例输出】
13
评测用例规模与约定】
对于 20% 的评测用例，1 ≤ N ≤ 10；
对于所有评测用例，1 ≤ N ≤ 1000000000。

题解
1.用dp先打表，然后遍历即可，当然数组别开大了，别贪，一般开1000，能过一半
2.找规律 斜着看

试题 I: 双向排序

时间限制: 5.0s 内存限制: 512.0MB 本题总分：25 分
【问题描述】
给定序列 (a1, a2, · · · , an) = (1, 2, · · · , n)，即 ai = i。
小蓝将对这个序列进行 m 次操作，每次可能是将 a1, a2, · · · , aqi 降序排列，
或者将 aqi
, aqi+1, · · · , an 升序排列。
请求出操作完成后的序列。
【输入格式】
输入的第一行包含两个整数 n, m，分别表示序列的长度和操作次数。
接下来 m 行描述对序列的操作，其中第 i 行包含两个整数 pi
, qi 表示操作
类型和参数。当 pi = 0 时，表示将 a1, a2, · · · , aqi 降序排列；当 pi = 1 时，表示
将 aqi
, aqi+1, · · · , an 升序排列。
【输出格式】
输出一行，包含 n 个整数，相邻的整数之间使用一个空格分隔，表示操作
完成后的序列。
【样例输入】
3 3
0 3
1 2
0 2
【样例输出】
3 1 2
【样例说明】
原数列为 (1, 2, 3)。
第 1 步后为 (3, 2, 1)。
第 2 步后为 (3, 1, 2)。
第 3 步后为 (3, 1, 2)。与第 2 步操作后相同，因为前两个数已经是降序了。
【评测用例规模与约定】
对于 30% 的评测用例，n, m ≤ 1000；
对于 60% 的评测用例，n, m ≤ 5000；
对于所有评测用例，1 ≤ n, m ≤ 100000，0 ≤ ai ≤ 1，1 ≤ bi ≤ n。

题解:
1.暴力，直接用自带的api，会更快，sort(str[],start,end)注意语法，对str数组的[start,end)排序
2.线段树 任意能做到logn更新的数据结构即可，同时由于本题的特殊性，甚至可用栈完成，但不易想到，不如直接数据结构

试题 J: 括号序列

时间限制: 5.0s 内存限制: 512.0MB 本题总分：25 分
【问题描述】
给定一个括号序列，要求尽可能少地添加若干括号使得括号序列变得合法，
当添加完成后，会产生不同的添加结果，请问有多少种本质不同的添加结果。
两个结果是本质不同的是指存在某个位置一个结果是左括号，而另一个是右括
号。
例如，对于括号序列 ((()，只需要添加两个括号就能让其合法，有以下几
种不同的添加结果：()()()、()(())、(())()、(()()) 和 ((()))。
【输入格式】
输入一行包含一个字符串 s，表示给定的括号序列，序列中只有左括号和
右括号。
【输出格式】
输出一个整数表示答案，答案可能很大，请输出答案除以 1000000007 (即
109 + 7) 的余数。
【样例输入】
((()
【样例输出】
5
【评测用例规模与约定】
对于 40% 的评测用例，|s| ≤ 200。
对于所有评测用例，1 ≤ |s| ≤ 5000。

题解：
1.dp

格外的：

试题 H: 左孩子右兄弟

时间限制: 2.0s 内存限制: 512.0MB 本题总分：20 分
【问题描述】
对于一棵多叉树，我们可以通过 “左孩子右兄弟” 表示法，将其转化成一棵
二叉树。
如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。
换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。
给定一棵包含 N 个结点的多叉树，结点从 1 至 N 编号，其中 1 号结点是
根，每个结点的父结点的编号比自己的编号小。请你计算其通过 “左孩子右兄
弟” 表示法转化成的二叉树，高度最高是多少。注：只有根结点这一个结点的
树高度为 0 。
例如如下的多叉树：

可能有以下 3 种 (这里只列出 3 种，并不是全部) 不同的 “左孩子右兄弟”
表示：

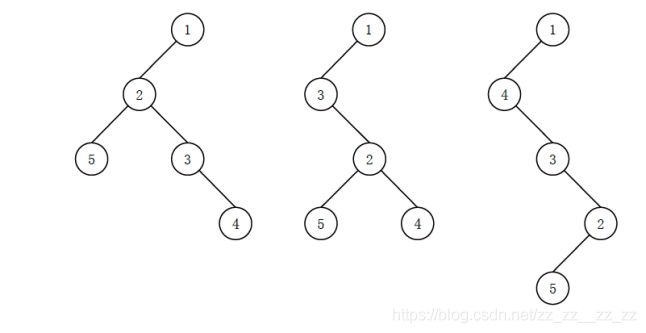
其中最后一种高度最高，为 4。
【输入格式】
输入的第一行包含一个整数 N。
以下 N −1 行，每行包含一个整数，依次表示 2 至 N 号结点的父结点编号。
【输出格式】
输出一个整数表示答案。
【样例输入】
5
1
1
1
2
【样例输出】
4
【评测用例规模与约定】
对于 30% 的评测用例，1 ≤ N ≤ 20；
对于所有评测用例，1 ≤ N ≤ 100000。

题解：树状dp 最大子节点+兄弟节点个数

import java.util.*;

public class Main {
    static List<Integer>[] a;
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        a=new List[n+1];
        for(int i=0;i<a.length;i++){
            a[i]=new ArrayList<>();
        }
        for(int i=2;i<=n;i++){
            int t=sc.nextInt();
            a[t].add(i);
        }
        System.out.println(dfs(1));
    }
    static int dfs(int x){
        int max=0;
        for(int i=0;i<a[x].size();i++){
            max=Math.max(dfs(a[x].get(i)),max);
        }
        return max+a[x].size();
    }
}