树与堆（基本概念及二叉树、二叉堆的python实现）

树

1.基本概念

• 什么是树？ 
  树是一种数据结构，可以表示层次关系。形状像一棵树。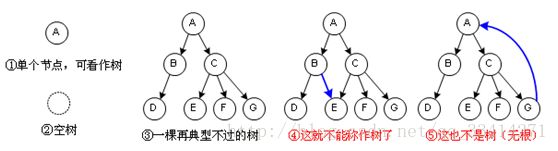 
   
  最上面；树根 
  中间：树枝 
  最下：树叶

• 树的定义 
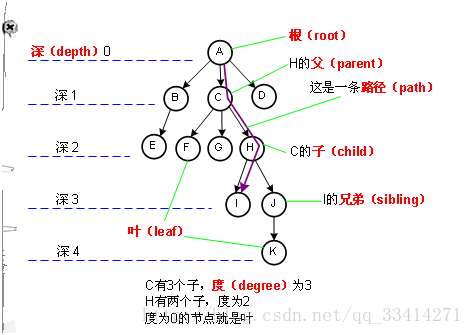
  它是由n（n>=1）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

  • 每个节点有零个或多个子节点
  • 没有父节点的节点称为根节点
  • 每一个非根节点有且只有一个父节点
  • 除了根节点外，每个子节点可以分为多个不相交的子树。

  注：可以是一对多，但一个子节点只能有一个父节点 
  

2.树的分类

数据结构中有很多树的结构，其中包括二叉树、二叉搜索树、2-3树、红黑树等等。其中二叉树是数据结构中一种重要的数据结构，也是树表家族最为基础的结构。

二叉树的定义

二叉树的定义：二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有2i-1个结点；深度为k的二叉树至多有2k-1个结点；对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点数为n2，则n0=n2+1。

二叉树的示例： 

满二叉树和完全二叉树

满二叉树 
满二叉树：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点。也可以这样理解，除叶子结点外的所有结点均有两个子结点。节点数达到最大值，所有叶子结点必须在同一层上。 
满二叉树的性质： 
1) 一颗树深度为h，最大层数为k，深度与最大层数相同，k=h; 
2) 叶子数为2h; 
3) 第k层的结点数是：2k-1; 
4) 总结点数是：2k-1，且总节点数一定是奇数。

完全二叉树 
完全二叉树：若设二叉树的深度为h，除第 h 层外，其它各层 (1～(h-1)层) 的结点数都达到最大个数，第h层所有的结点都连续集中在最左边，这就是完全二叉树。 

注：完全二叉树是效率很高的数据结构，堆是一种完全二叉树或者近似完全二叉树，所以效率极高，像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化，二叉排序树的效率也要借助平衡性来提高，而平衡性基于完全二叉树。

完全二叉树的性质： 
1) 在非空二叉树中，第i层的结点总数不超过2i-1, i>=1; 
2) 深度为h的二叉树最多有2h-1个结点(h>=1)，最少有h个结点; 
3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1; 
4) 具有n个结点的完全二叉树的深度为log2(n+1); 
5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系： 
若I为结点编号则 如果I>1，则其父结点的编号为I/2； 
如果2I<=N，则其左儿子（即左子树的根结点）的编号为2I；若2I>N，则无左儿子； 
如果2I+1<=N，则其右儿子的结点编号为2I+1；若2I+1>N，则无右儿子。 
6)给定N个节点，能构成h(N)种不同的二叉树，其中h(N)为卡特兰数的第N项，h(n)=C(2*n, n)/(n+1)。 
7)设有i个枝点，I为所有枝点的道路长度总和，J为叶的道路长度总和J=I+2i。

3..树的基本操作

遍历：前中后序遍历；层次遍历 
序列化与反序列化 
深度：最大深度，最小深度

4.二叉树的遍历

遍历即将树的所有结点访问且仅访问一次。按照根节点位置的不同分为前序遍历，中序遍历，后序遍历。

• 前序遍历：根节点->左子树->右子树
• 中序遍历：左子树->根节点->右子树
• 后序遍历：左子树->右子树->根节点

例如：求下面树的三种遍历 
 
前序遍历：abdefgc 
中序遍历：debgfac 
后序遍历：edgfbca

5.二叉树的遍历的实现

二叉树的生成

下面是一个完全二叉树的生成方法：

    '''添加元素'''
    def add(self,data):
        node=Node(data)
        if self.root.data==None:
            self.root=node
            #在队列第一个位置加入左右子树没有满的节点
            self.myQueen.append(self.root)
        else:
            treeNode=self.myQueen[0]
            print('treenode',treeNode.data)

            if treeNode.lchild==None:
                if(node.data is None):
                    return
                treeNode.lchild=node
                self.myQueen.append(treeNode.lchild)
            else : 
                treeNode.rchild=node
                self.myQueen.append(treeNode.rchild)
                self.myQueen.pop(0)

非完全二叉树（如下图）： 

构造方法：

class Node(object):
    def __init__(self,data=None,lchild=None,rchild=None):
        self.data=data
        self.lchild=lchild
        self.rchild=rchild

class BTree(object):
    def __init__(self,root):
        self.root=root

node1=Node(4)
node2=Node(5)
ndee3=Node(3,node1,node2)
node4=Node(1,None,ndee3)
tree=BTree(node4)

另一种构造方法：

class Node(object):
    def __init__(self,data=None,lchild=None,rchild=None):
        self.data=data
        self.lchild=lchild
        self.rchild=rchild
class BTree(object):
    def __init__(self,root=None):
        self.root=root

     def create(self,arr):
        temp=arr.pop(0) 

        print(temp)         
        if temp is '#':
            return

        treenode = Node(data=temp)

        if self.root is None:
            self.root = treenode
        treenode.lchild = self.create(arr)
        treenode.rchild = self.create(arr)
        return treenode

tree=BTree()
arr=[1,'#',3,4,'#','#',5,'#','#']
tree2=tree.create(arr)
tree.front_recursion(tree2)
tree.middle_recursion(tree2)
tree.back_recursion(tree2)

一个完整的代码示例：

# -*- coding: utf-8 -*-

class Node(object):
    def __init__(self,data=None):
        self.data=data
        self.lchild=None
        self.rchild=None

class BinaryTree(object):
    def __init__(self):
        self.root=Node()
        self.myQueen=[]

    '''添加元素'''
    def add(self,data):
        node=Node(data)
        if self.root.data==None:
            self.root=node
            #在队列第一个位置加入左右子树没有满的节点
            self.myQueen.append(self.root)
        else:
            treeNode=self.myQueen[0]
            if treeNode.lchild==None:
                treeNode.lchild=node
                self.myQueen.append(treeNode.lchild)
            else :
                treeNode.rchild=node
                self.myQueen.append(treeNode.rchild)
                self.myQueen.pop(0)

    '''前序递归遍历'''
    def front_recursion(self,root):
        if root==None:
            return
        print(root.data)
        self.front_recursion(root.lchild)
        self.front_recursion(root.rchild)

    '''中序递归遍历'''
    def middle_recursion(self,root):
        if root==None:
            return
        self.middle_recursion(root.lchild)
        print(root.data)
        self.middle_recursion(root.rchild)

    '''后序递归遍历'''
    def back_recursion(self,root):
        if root==None:
            return
        self.back_recursion(root.lchild)
        self.back_recursion(root.rchild)
        print(root.data)

if __name__=='__main__':
    tree=BinaryTree()
    for i in range(10):
        tree.add(i)
    print('前序递归遍历')
    tree.front_recursion(tree.root)
    print('中序递归遍历')
    tree.middle_recursion(tree.root)
    print('后序递归遍历')
    tree.back_recursion(tree.root)      

其中myQueen表是目前左右子树没有满的节点，且每次从第一个开始取，左右子树满了之后将第一个删除

堆

1. 基本概念

堆的实现通过构造二叉堆（binary heap），实为二叉树的一种；由于其应用的普遍性，当不加限定时，均指该数据结构的这种实现。

堆常用来实现优先队列，在这种队列中，待删除的元素为优先级最高（最低）的那个。在任何时候，任意优先元素都是可以插入到队列中去的，是计算机科学中一类特殊的数据结构的统称

最大（最小）堆是一棵每一个节点的键值都大于（小于）其子节点键值的树。大顶堆是一棵完全二叉树，同时也是一棵最大树。小顶堆是一棵完全完全二叉树，同时也是一棵最小树。 
注意： 
· 堆中任一子树亦是堆。 
· 以上讨论的堆实际上是二叉堆(Binary Heap)，类似地可定义k叉堆。 
下图分别给出最大堆和最小堆的例子：

2..堆支持的基本操作:

• create: 建立一个空堆；
• insert: 向堆中插入一个新元素；
• get：获取当前堆顶元素的值；
• pop：删除堆顶元素；

某些堆实现还支持其他的一些操作，如斐波那契堆支持检查一个堆中是否存在某个元素。

3.最小二叉堆的实现

存储——数组

用数组来存储二叉堆，其中： 
已知元素位置i：则其左子节点位置为2*（i+1）-1，右子节点位置为 2 *（i+1），父节点位置为math.floor((i-1)/2)

注：floor表示向下取整

新元素加入——bubble_up方法

新元素加入时，添加到数组最后一个，然后不断向上找最小的（最大堆情况），不断向跟父节点判断，直到父节点大于新加入的元素或已经置顶（最大堆）

    def bubble_up(self,i):
        p_index=self.parent(i)
        #如果没有父节点，直接返回
        if p_index==-1:return True
        #如果父节点比当前节点小，交换这两个节点数据
        p_data=self._data[p_index]
        data=self._data[i]
        if p_data

删除堆顶元素——bubble_down方法

删除堆顶元素相当于删除数组中第一个元素 
将最后一个元素不断跟其子节点比较，比子节点小的话就向下移动（最大堆）

    def bubble_down(self,i):
        lc_index=self.lchild(i)
        rc_index=self.rchild(i)
        if not (lc_index==-1 and rc_index==-1):
            #选择一个最大的子节点
            if rc_index==-1 or (self._data[lc_index]>self._data[rc_index]):#左边大
                rep_index=lc_index
            elif lc_index==-1 or (self._data[lc_index]<=self._data[rc_index]):#右边大
                rep_index=rc_index
            rep_data= self._data[rep_index]
            data=self._data[i]

            if rep_data>data:
                self._data[rep_index]=data
                self._data[i]=rep_data
                self.bubble_down(rep_index)
            #如果没有子节点，返回TRUE
        else:
            return True

让二叉堆的时间复杂度为O（n）

如果直接每插入一个节点就将节点向上比较，时间复杂度为其时间复杂度为 O(n*log n)

更有效的方法： 
先存储为数组（没有执行构造二叉堆的操作） 
从下层开始，让每个子堆有序 
不断向上移动

def build_eff_heap(total_num):
    heap=MaxHeap()
    for i in range(total_num):
        heap._data.append(i)
    #math.floor表示向下取整
    for i in range(math.floor(len(heap._data)/2)-1,-1,-1):
        heap.bubble_down(i)#倒数第二层开始跟子节点比较
    return heap

运行效果比较

完整的最大堆创建和测试代码（最大堆）：

# -*- coding: utf-8 -*-

import math
import time

class ArrBinHeap:
    '''初始化'''
    def __init__(self):
        self._data=[]  #表示二叉树

    '''
    插入的节点往上移
    取决于最大堆还是最小堆
    '''
    def bubble_up(self,i):
        pass    

    '''
    节点往下移
    '''
    def bubble_down(self,i):
        pass  

    '''插入'''
    def insert(self,val):
        self._data.append(val)
        self.bubble_up(len(self._data)-1)

    '''
    删除最大或最小的一个数
    用最后一个节点的值替代
    最后一个节点往下移动bubble_down
    '''
    def pop(self):
        last_index=len(self._data)-1
        last_data=self._data[last_index]
        self._data=self._data[:last_index-1]
        self._data[0]=last_data
        self.bubble_down(0)

    '''已知节点位置i，返回左子节点'''
    def lchild(self,i):
        index=2*(i+1)-1
        #检查是否超出范围
        if len(self._data)<=index:
            return -1
        return index
        '''已知节点位置i，返回左子节点'''

    '''已知节点位置i，返回左子节点'''
    def rchild(self,i):
        index=2*(i+1)
        #检查是否超出范围
        if len(self._data)<=index:
            return -1
        return index

    '''找父节点'''
    def parent(self,i):
        return math.floor((i-1)/2)

    '''获得堆顶元素'''
    def get(self):
        if self._data[0]!=None:
            return self._data[0]

class MaxHeap(ArrBinHeap):
    def __init__(self):
        super(MaxHeap,self).__init__()

    def bubble_up(self,i):
        p_index=self.parent(i)
        #如果没有父节点，直接返回
        if p_index==-1:return True
        #如果父节点比当前节点小，交换这两个节点数据
        p_data=self._data[p_index]
        data=self._data[i]
        if p_dataself._data[rc_index]):#左边大
                rep_index=lc_index
            elif lc_index==-1 or (self._data[lc_index]<=self._data[rc_index]):#右边大
                rep_index=rc_index
            rep_data= self._data[rep_index]
            data=self._data[i]

            if rep_data>data:
                self._data[rep_index]=data
                self._data[i]=rep_data
                self.bubble_down(rep_index)
            #如果没有子节点，返回TRUE
        else:
            return True

        return True

def build_heap(total_num):
    heap=MaxHeap()
    for i in range(total_num):
        heap.insert(i)
    return heap
def build_eff_heap(total_num):
    heap=MaxHeap()
    for i in range(total_num):
        heap._data.append(i)
    #math.floor表示向下取整
    for i in range(math.floor(len(heap._data)/2)-1,-1,-1):
        heap.bubble_down(i)
    return heap

if __name__=="__main__":
    start_time=time.time()
    heap=build_heap(1000000)
    maxnum= heap.get()
    print('堆顶元素为：',maxnum)
    heap.pop()
    maxnum= heap.get()
    print('pop后堆顶元素为：',maxnum)
    print('---%s seconds---'%(time.time()-start_time))

    start_time=time.time()
    heap=build_eff_heap(1000000)
    maxnum= heap.get()
    print('堆顶元素为：',maxnum)

    heap.pop()
    maxnum= heap.get()
    print('pop后堆顶元素为：',maxnum)
    print('---%s seconds---'%(time.time()-start_time))

参考文献 
[树的概念] http://blog.csdn.net/qq20004604/article/details/50936940 
[数据结构中的各种树]http://www.cnblogs.com/maybe2030/p/4732377.html 
[堆]http://blog.csdn.net/wypblog/article/details/8076324 
[二叉树]http://blog.csdn.net/fansongy/article/details/6798278 
[二叉树的遍历]http://blog.csdn.net/bone_ace/article/details/46718683 
[二叉堆的实现]https://www.bilibili.com/video/av11865315