机器学习算法入门梳理——决策树的分类预测详解
基于决策树的分类预测
机器学习算法详解,day2 打卡!
- 决策树概念
- 信息熵
- 基尼系数
- 剪枝
- 总结
1. 决策树的概念
决策树(decision tree)也是机器学习中的一个重要算法,但是我们可能平时在决策的时候就常常用到,比如以下天气和怎么出行的问题:
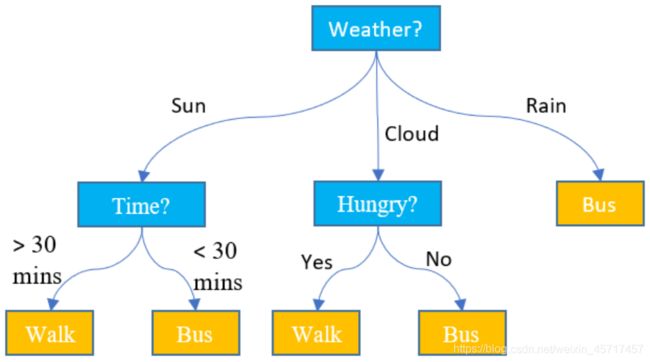
决策树是一种非参数学习算法,可以解决分类(包括多分类)问题,还可以解决回归问题。
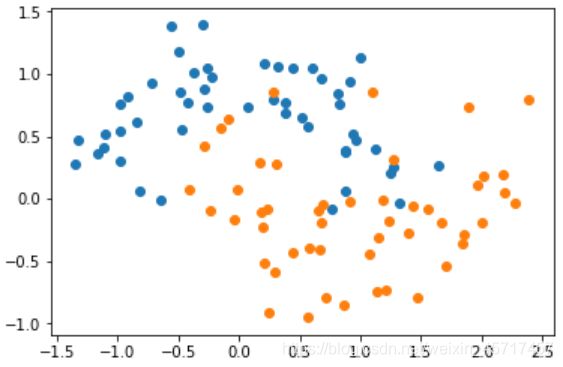
如下的例子,用 iris 简单看一下决策树。
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
iris_all = pd.DataFrame(data=iris.data, columns=iris.feature_names).copy()
# target = iris.target
iris_all['target'] = iris.target
# 为了方便可视化,仅使用两个特征
iris = iris_all.iloc[:,2:]
sns.scatterplot(data=iris, x = iris.columns.values[0], y = iris.columns.values[1],hue='target',palette="Set1")
plt.show()
# 决策边界函数
def plot_boundary(model, X, y):
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
h = .02 # step size in the mesh
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1, figsize=(4, 3))
plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Set3_r)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap=plt.cm.Accent)
plt.show()
from sklearn.tree import DecisionTreeClassifier
np.random.seed(2)
iris = datasets.load_iris()
X = iris.data[:,2:]
y = iris.target
dt_clf = DecisionTreeClassifier(max_depth=2, criterion='entropy',) # max_depth 最大深度;criterion选择熵
dt_clf.fit(X, y)
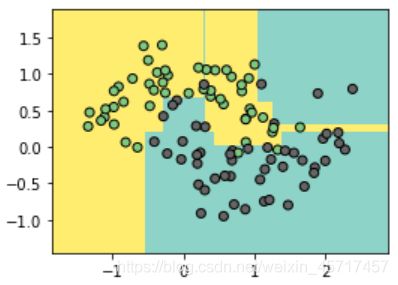
plot_boundary(dt_clf, X, y)
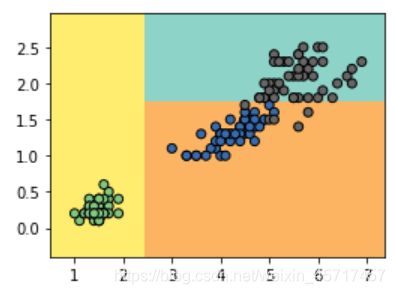
以上其实就是一个决策树,当 x < 2.4 时,被分为黄色的一类;其余再进行判断,如果 y < 1.8 ,则是橘色的一类,y > 1.8 则是青色的一类。
2. 信息熵
在决策树中,每个节点在哪里划分,是如何确定呢?
信息熵(information entropy)是一种判断方法。熵是信息论中衡量随机变量不确定度的,这个值越大则数据的不确定性越高;反之,越小则数据的不确定性越低。信息熵是度量样本集合纯度最常用的一个指标,假如当前样本集合 D 中第 i 类样本所占的比例为 p i p_i pi ,则 D 的信息熵为:
H = − ∑ i = 1 k p k l o g 2 p i H = -\sum_{i=1}^{k}p_klog_2p_i H=−i=1∑kpklog2pi
假如有一个集合,有三类样本,比例分别为 { 1 3 , 1 3 , 1 3 } \{\frac{1}{3},\frac{1}{3},\frac{1}{3}\} {31,31,31} ,那么可求得信息熵为:
H = − 1 3 l o g 2 ( 1 3 ) − 1 3 l o g 2 ( 1 3 ) − 1 3 l o g 2 ( 1 3 ) = 1.585 H = -\frac{1}{3}log_2\left(\frac{1}{3}\right)-\frac{1}{3}log_2\left(\frac{1}{3}\right)-\frac{1}{3}log_2\left(\frac{1}{3}\right)=1.585 H=−31log2(31)−31log2(31)−31log2(31)=1.585
假如还有另一个集合,三个分类比例为 { 1 10 , 2 10 , 7 10 } \{\frac{1}{10},\frac{2}{10},\frac{7}{10}\} {101,102,107} ,则信息熵为:
H = − 1 10 l o g 2 ( 1 10 ) − 2 10 l o g 2 ( 2 10 ) − 7 10 l o g 2 ( 7 10 ) = 1.157 H = -\frac{1}{10}log_2\left(\frac{1}{10}\right)-\frac{2}{10}log_2\left(\frac{2}{10}\right)-\frac{7}{10}log_2\left(\frac{7}{10}\right)=1.157 H=−101log2(101)−102log2(102)−107log2(107)=1.157
第二个集合比第一个集合的信息熵要小。第一个集合的比例都一致,更不确定哪个分类。
假如集合分类是 { 1 , 0 , 0 } \{1,0,0\} {1,0,0} ,那么信息熵可求得为0。
当仅有两个分类时,一个分类的比例为 x ,则另一个则为 1 - x ,那么公式为:
H = − x l o g x ( x ) − ( 1 − x ) l o g ( 1 − x ) H = -xlog_x\left(x\right) - \left(1-x\right)log\left(1-x\right) H=−xlogx(x)−(1−x)log(1−x)
可视化为:
def entropy(p):
return -p * np.log2(p) - (1-p) * np.log2(1-p)
x = np.linspace(0.001, 0.999, 1000)
plt.plot(x, entropy(x))
plt.show()
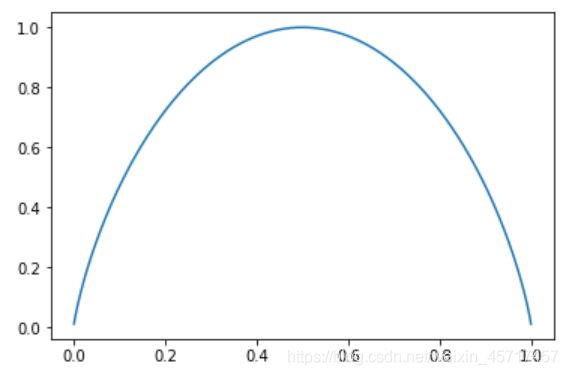
关于信息熵的更加系统和详细的理论知识,由于时间和空间的关系,无法在此展开。推荐大家关注B站up主:fcieee(上海某西南高校教授)。他所讲授的《信息论》课程很新、很接地气、很清晰,推荐指数:满星!
3. 基尼系数
基尼系数(Gini)是另外一种判断方法,其公式为:
G = 1 − ∑ i = 1 k p i 2 G = 1-\sum_{i=1}^{k}p_i^2 G=1−i=1∑kpi2
同样是像上面的三个例子,它们的基尼系数分别为:
G 1 = 1 − ( 1 3 ) 2 − ( 1 3 ) 2 − ( 1 3 ) 2 = 0.66 G 2 = 1 − ( 1 10 ) 2 − ( 2 10 ) 2 − ( 7 10 ) 2 = 0.46 G 3 = 0 G1 = 1-\left(\frac{1}{3}\right)^2-\left(\frac{1}{3}\right)^2-\left(\frac{1}{3}\right)^2 = 0.66\\ G2 = 1-\left(\frac{1}{10}\right)^2-\left(\frac{2}{10}\right)^2-\left(\frac{7}{10}\right)^2 = 0.46\\ G3 = 0 G1=1−(31)2−(31)2−(31)2=0.66G2=1−(101)2−(102)2−(107)2=0.46G3=0
与上面类似,当基尼系数为 0 时,分类是确定的。当仅有两个分类时,一个分类的比例为 x ,则另一个则为 1 - x ,那么公式为:
G = 1 − x 2 − ( 1 − x ) 2 = − 2 x 2 + 2 x G = 1-x^2-\left(1-x\right)^2=-2x^2+2x G=1−x2−(1−x)2=−2x2+2x
这条抛物线的对称轴也是 1/2 ,在 1/2 时,信息熵为 0 ,分类最不确定。
from sklearn.tree import DecisionTreeClassifier
np.random.seed(2)
iris = datasets.load_iris()
X = iris.data[:,2:]
y = iris.target
dt_clf = DecisionTreeClassifier(max_depth=2, criterion='gini') # 改成gini系数
dt_clf.fit(X, y)
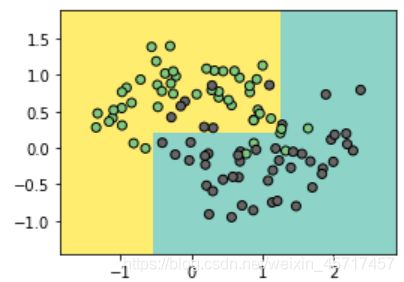
plot_boundary(dt_clf, X, y)
4. 剪枝
CART (classification and regression tree),这是一种创建决策树的方法,即根据某一个维度和某一个阈值进行二分。
X, y = datasets.make_moons(noise = 0.25, random_state=666)
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
dt_clf = DecisionTreeClassifier()
dt_clf.fit(X,y)
plot_boundary(dt_clf, X, y)
可以看到明显的过拟合现象。
dt_clf2 = DecisionTreeClassifier(max_depth=2)
dt_clf2.fit(X,y)
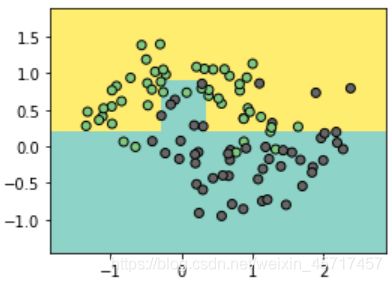
plot_boundary(dt_clf2, X, y)

当我们限制深度的时候,可以看到没有过拟合现象了,不过这种情况可能存在欠拟合现象。所以需要调整一下相关的参数。
# min_samples_split
# 对于一个节点,至少需要多少样本数据
# 这个参数越大时,则越不容易发生过拟合,不过过大可能会发生欠拟合
dt_clf3 = DecisionTreeClassifier(min_samples_split=10)
dt_clf3.fit(X,y)
plot_boundary(dt_clf3, X, y)
dt_clf3 = DecisionTreeClassifier(min_samples_split=20)
dt_clf3.fit(X,y)
plot_boundary(dt_clf3, X, y)
# min_samples_leaf
# 对于叶子节点至少有几个样本
# 这个值越大也是可以避免过拟合
dt_clf4 = DecisionTreeClassifier(min_samples_leaf=1)
dt_clf4.fit(X,y)
plot_boundary(dt_clf4, X, y)
dt_clf4 = DecisionTreeClassifier(min_samples_leaf=6)
dt_clf4.fit(X,y)
plot_boundary(dt_clf4, X, y)
5. 总结
决策树是一种常见的分类模型,在金融分控、医疗辅助诊断等诸多行业具有较为广泛的应用。决策树的核心思想是基于树结构对数据进行划分,这种思想是人类处理问题时的本能方法。例如在婚恋市场中,女方通常会先看男方是否有房产,如果有房产再看是否有车产,如果有车产再看是否有稳定工作……最后得出是否要深入了解的判断。
决策树的主要优点:
1、具有很好的解释性,模型可以生成可以理解的规则。
2、可以发现特征的重要程度。
3、模型的计算复杂度较低。
决策树的主要缺点:
1、模型容易过拟合,需要采用减枝技术处理。
2、不能很好利用连续型特征。
3、预测能力有限,无法达到其他强监督模型效果。
4、方差较高,数据分布的轻微改变很容易造成树结构完全不同。
由于决策树模型中自变量与因变量的非线性关系以及决策树简单的计算方法,使得它成为集成学习中最为广泛使用的基模型。梯度提升树(GBDT),XGBoost以及LightGBM等先进的集成模型都采用了决策树作为基模型,在广告计算、CTR预估、金融风控等领域大放异彩,成为当今与神经网络相提并论的复杂模型,更是数据挖掘比赛中的常客。在新的研究中,南京大学周志华老师提出一种多粒度级联森林模型,创造了一种全新的基于决策树的深度集成方法,为我们提供了决策树发展的另一种可能。
同时决策树在一些需要明确可解释甚至提取分类规则的场景中被广泛应用,而其他机器学习模型在这一点很难做到。例如在医疗辅助系统中,为了方便专业人员发现错误,常常将决策树算法用于辅助病症检测。例如在一个预测哮喘患者的模型中,医生发现测试的许多高级模型的效果非常差。所以他们在数据上运行了一个决策树的模型,发现算法认为剧烈咳嗽的病人患哮喘的风险很小。但医生非常清楚剧烈咳嗽一般都会被立刻检查治疗,这意味着患有剧烈咳嗽的哮喘病人都会马上得到收治。用于建模的数据认为这类病人风险很小,是因为所有这类病人都得到了及时治疗,所以极少有人在此之后患病或死亡。
参考资料:
- 阿里云notebook:https://developer.aliyun.com/ai/scenario/bb2fe211e5e94017840ce42cc31fe621
- 小白学习决策树视频:https://www.bilibili.com/video/BV1eV411U7Ke