线性回归与感知机分类
线性回归模型
scikit-learn 中包含的线性模型有最小二乘回归、感知机、逻辑回归、岭回归,贝叶斯回归等,由 sklearn.linear_model 模块导入。线性模型其实就是通过拟合线性函数(下图)去完成样本分类或回归预测。
其中,最小二乘回归、岭回归、贝叶斯回归等是用于解决回归问题。而感知机、逻辑回归被用于解决分类问题。
这里,我们从比较基础的 最小二乘法 回归说起。最小二乘法是线性回归中最经典的方法之一,最小二乘的取名即来自于平方损失函数。在 scikit-learn 中,最小二乘法的估计器如下:
在最小二乘回归中,不涉及数据处理的情况下,我们使用 scikit-learn 完成该任务只需三步:
选择相应的估计器构建相应的模型 model,并设置模型参数。
使用该估计器型提供的 model.fit() 方法训练模型。
使用该估计器提供的 model.predict() 方法用于预测。
下面,举个简单的例子,我们通过最小二乘回归去拟合二维平面上的一些点。首先,执行上面的第一步,载入估计器并构建模型,其中 warning 模块通常用于警告用户一些错误或者过时的用法,这里用 warnings.filterwarnings('ignore') 是为了忽略警告,仅供教学方便,自行书写代码时警告也很重要,不建议忽略。
import warnings
from sklearn.linear_model import LinearRegression
warnings.filterwarnings('ignore')
model = LinearRegression() # 调用最小二乘线性回归(第 1 步)
model
接下来,使用模型带有的 fit() 方法去拟合 3 个点。三个点的特征向量分别为 [0, 0], [1, 1], [2, 2],对应的目标值为 [1, 2, 3]。
model.fit([[0, 0], [1, 1], [2, 2]], [1, 2, 3]) # 模型训练(第 2 步)
当然,我们也可以从这一步看到模型返回的参数。
训练时,选择的 [0, 0], [1, 1], [2, 2]这三个点恰好在一条直线上,再结合目标值想象一下它们的空间位置关系。我们可以使用 model.coef_, 输出拟合直线 w项,使用 model.intercept_ 输出常数项值。
model.coef_, model.intercept_
如上所示,即实验拟合的函数应该为:
当我们输入新的数值,例如 [3, 3]时,根据上面的函数,因变量的值为4。那么,我们使用模型来预测,看一看结果是否为4。
model.predict([[3, 3]]) # 模型预测(第 3 步)
结果的确和我们预想的一致,也标志着我们通过 scikit-learn 完成了一个基础的线性回归问题,而建模的过程仅仅需要简单的 3 步。
上面的例子比较简单,下面我们导入 scikit-learn 内置的 diabetes 糖尿病数据集来训练一个复杂一点的最小二乘回归模型。
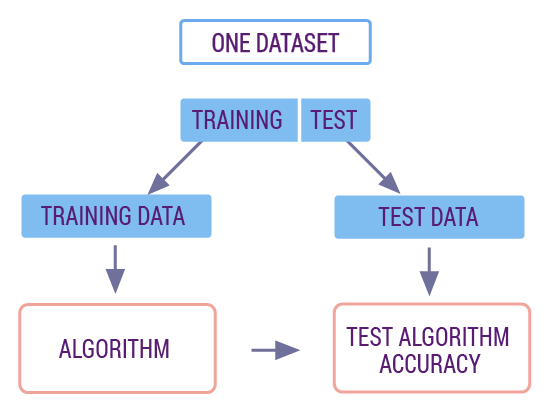
第一步:导入数据,并将其划分为 70% 的训练集和 30% 的测试集。机器学习中,我们习惯采用这样的比例来划分训练集和测试集。其中训练集用来训练模型,而测试集则用来评估模型。测试集的数据不会出现在训练数据中,这也就类似我们使用了新的数据对训练好的模型进行预测和评估,以保证模型质量真实可靠。
下面我们会用到 train_test_split 模块,其参数 test_size 表示切割比例,random_state 设置随机数种子,保证每次随机数结果相同。
from sklearn import datasets # 导入内置数据集模块
from sklearn.model_selection import train_test_split # 导入数据集切分模块
import numpy as np # 导入数值计算模块
diabetes = datasets.load_diabetes() # 载入糖尿病数据集
print(diabetes.keys())
print(diabetes.data.shape)
# 该数据集的特征有十个,这里只选取第三列的那一个,np.newaxis 为切片后的数据增加一个维度
diabetes_feature = diabetes.data[:, np.newaxis, 2]
diabetes_target = diabetes.target # 设定目标值
print(diabetes_feature.shape)
# 切分数据集为 70% 的训练集和 30% 的预测集
train_feature, test_feature, train_target, test_target = train_test_split(
diabetes_feature, diabetes_target, test_size=0.3, random_state=56)
第二步:载入最小二乘回归估计器,并训练数据。这一步想必通过上面的例子已经清楚了,注意这里传入的是训练数据。
model = LinearRegression() # 构建最小二乘线性回归模型
model.fit(train_feature, train_target) # 使用训练集数据训练模型
第三步:使用 model.predict() 对测试集进行预测,并将结果绘图。
import matplotlib.pyplot as plt # 导入 matplotlib 绘图模块
%matplotlib inline
# 绘图
plt.scatter(train_feature, train_target, color='black') # 绘制训练集散点图
plt.scatter(test_feature, test_target, color='red') # 绘制测试集散点图
plt.plot(test_feature, model.predict(test_feature),
color='blue', linewidth=3) # 使用测试集进行预测并绘制拟合直线
# 绘制图例
plt.legend(('Fit line', 'Train Set', 'Test Set'), loc='lower right')
plt.title('LinearRegression Example')
如上图所示,我们可以更加直观地看出采用最小二乘回归进行线性拟合的结果。
对于其他常见的线性回归模型,它们和最小二乘线性回归模型非常相似,只是采用了不同的损失函数。
例如,岭回归采用了带 L2 惩罚项的平方和损失函数。
而另一种常见的 Lasso 回归,采用了带 L1 惩罚项的平方损失函数。
下面列举了一些常见的广义线性回归模型,及它们在 scikit-learn 中对应的估计器。
这些方法相对于普通最小二乘回归模型而言,均增加了一些惩罚项,这样会提高模型的泛化能力,在实际应用中效果可能会好一些。有一些方法我们会在实验五中做统一的比较。
线性分类模型
除了线性回归,scikit-learn 还提供了一些解决线性分类的方法。其中,感知机就是非常有代表性的线性分类模型。
感知机 是一个经典的二分类方法,由 Rosenblatt 于 1957 年时提出。它是神经网络和支持向量机的基础。感知机模型非常简单,输入为一些特征向量,输出则由正类和负类组成。而输入和输出之间,则是由符号函数sign(x) 连接。
感知机的损失函数是错误分类点到分离超平面之间的距离总和,其学习策略同样也是损失函数最小化。
在 scikit-learn 中,实现感知机通过 sklearn.linear_model.Perceptron() 估计器完成。
下面,我们通过一个例子来展示感知机的分类过程。首先,使用 scikit-learn 提供的 make_classification 分类生成器生成一组可被二分类的二维数组作为数据集,其参数 n_samples 默认值为 100,n_features 总特征数量,n_classes 默认值为 2,即两类或两个标签。
from sklearn.datasets import make_classification # 导入分类数据生成模块
# 随机生成一组可以被二分类的数据
X, y = make_classification(n_features=2, n_redundant=0,
n_informative=1, n_clusters_per_class=1,
random_state=1)
# 查看数组形状
print(X.shape, y.shape)
print(y) # 查看 y 的返回值
这里,我们使用 Matplotlib 将该数据集绘制出来,直观上看看生成的数据集结构。
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y) # 绘制数据集散点图
我们可以看到,数据集分为 2 种颜色的样本点,并呈现出明显的线性界线。接下来,我们使用感知机对该数据集进行分类训练。
from sklearn.linear_model import Perceptron
# 将数据集划分为 70% 训练集和 30% 测试集
train_feature, test_feature, train_target, test_target = train_test_split(
X, y, test_size=0.3, random_state=56)
# 建立感知机模型,使用默认参数
model = Perceptron()
# 使用训练集训练模型
model.fit(train_feature, train_target)
训练结束后,我们将测试数据输入模型中,得到相应的预测结果。
preds = model.predict(test_feature) # 预测并得到预测结果
preds
然后将预测结果与真实结果进行比较,从而得到模型的分类准确度。
准确度表示正确预测的样本占全部样本的比例,是用于评估分类模型的常用指标之一,我们得到的 preds 是模型的预测结果,而真实结果为 test_target。接下来,可以通过 scikit-learn 提供的 accuracy_score 计算出分类准确度,我们会在最后一个实验详细介绍有关于验证评估的相关方法。
from sklearn.metrics import accuracy_score
accuracy_score(test_target, preds) # 先传入真实值,再传入预测值
返回的结果即是测试集预测分类准确度,如果为 1.0 则表示预测全部正确,分类准确度为 100%。
下面,我们使用 Matplotlib 将训练数据和测试数据绘制在原图上,并绘制出感知机分类时的决策边界。
# 创建一个绘图矩阵方便显示决策边界线
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
fig, ax = plt.subplots()
# 绘制决策边界
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, cmap=plt.cm.Paired)
# 绘制训练和测试数据
ax.scatter(train_feature[:, 0], train_feature[:, 1])
ax.scatter(test_feature[:, 0], test_feature[:, 1])
上图中,蓝色的为训练值,橙色的为测试值,可以看出分类完全正确,现在,我们就完成了一个简单的感知机分类实验。可以看出来,对于线性可分的二分类问题,感知机的预测效果还是很不错的。