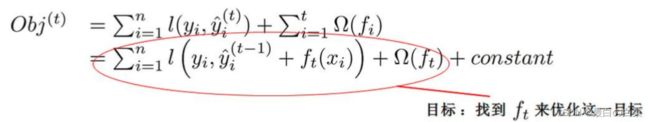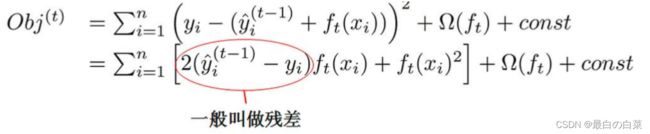Xgboost集成算法

Xgboost集成算法

学完神经网络之后，感觉脑子一片浆糊，大部分听不懂的状态，休息了三四天，还得继续向下学习。。。。唉，我就是太笨了啊！

xgboost介绍

xgboost算法是跟决策树联系在一起的

既可以做分类任务，也可以做回归任务。

${\hat{y}}_i={\sum }_j{w}_j{x}_{ij}$ 样本与权值的线性组合

目标函数：$l\left(y_i,{\hat{y}}_i\right)={\left(y_i-{\hat{y}}_i\right)}^2$
如何最优函数解？$F^{\ast }(x)=\arg \min E_{(x,y)}[L(y,F(x))]$
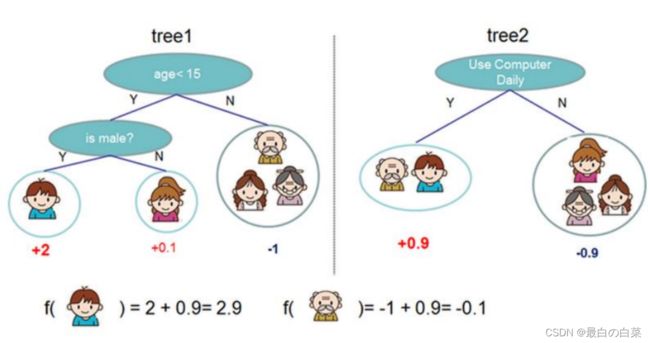
集成算法的表示：${\hat{y}}_i={\sum }_{k=1}^K{f}_k\left(x_i\right),f_k\in \mathcal{F}$

$\Omega \left(f_t\right)=\gamma T+\frac{1}{2}\lambda {\sum }_{j=1}^T{w}_{j=1}^2$ 前面限制叶子节点个数 后面是正则化惩罚项

$\Omega =\gamma 3+\frac{1}{2}\lambda (4+0.01+1)$

现在还剩下一个问题，我们如何选择每一轮加入什么f呢？答案是非常直接的，选取一个f来使得我们的目标函数尽量最大地降低

$\text{ 目标 }Ob{j}^{(t)}={\sum }_{i=1}^{n}l\left(y_i,{\hat{y}}_i^{(t-1)}+f_t\left(x_i\right)\right)+\Omega \left(f_t\right)+\text{ constant }$

用泰勒展开来近似我们原来的目标

泰勒展开: $f(x+\Delta x) \simeq f(x)+f^{\prime}(x) \Delta x+\frac{1}{2} f^{\prime \prime}(x) \Delta x^{2} $

定义:$ g_{i}=\partial_{\hat{y}^{(t-1)}} l\left(y_{i}, \hat{y}^{(t-1)}\right), \quad h_{i}=\partial_{\hat{y}^{(t-1)}}{2} l\left(y_{i}, \hat{y}^{(t-1)}\right) $

$Ob{j}^{(t)}\simeq {\sum }_{i=1}^n\left[l\left(y_i,{\hat{y}}_i^{(t-1)}\right)+g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_t^2\left(x_i\right)\right]+\Omega \left(f_t\right)+\text{ constant }$

${\sum }_{i=1}^n\left[g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_t^2\left(x_i\right)\right]+\Omega \left(f_t\right)$

$g_i={\partial }_{{\hat{y}}^{(t-1)}}l\left(y_i,{\hat{y}}^{(t-1)}\right),h_i={\partial }_{{\hat{y}}^{(t-1)}}^{2}l\left(y_i,{\hat{y}}^{(t-1)}\right)$

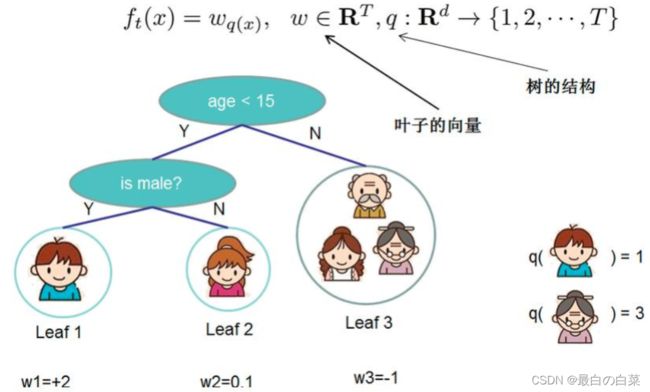
样本上遍历（i=1~n） 叶子节点上遍历(j=1~T)

$\begin{array}{rl}Ob{j}^{(t)}& \simeq \sum _{i=1}^n\left[g_i{f}_t\left(x_i\right)+\frac{1}{2}{h}_i{f}_t^2\left(x_i\right)\right]+\Omega \left(f_t\right)\\ & =\sum _{i=1}^n\left[g_i{w}_{q\left(x_i\right)}+\frac{1}{2}{h}_i{w}_{q\left(x_i\right)}^2\right]+\gamma T+\lambda \frac{1}{2}\sum _{j=1}^T{w}_j^2\\ & =\sum _{j=1}^T\left[\left(\sum _{i\in I_j}{g}_i\right)w_j+\frac{1}{2}\left(\sum _{i\in I_j}{h}_i+\lambda \right)w_j^2\right]+\gamma T\end{array}$

$G_j={\sum }_{i\in I_j}{g}_i{H}_j={\sum }_{i\in I_j}{h}_i$

$\begin{array}{l}Ob{j}^{(t)}={\sum }_{j=1}^T\left[\left({\sum }_{i\in I_j}{g}_i\right)w_j+\frac{1}{2}\left({\sum }_{i\in I_j}{h}_i+\lambda \right)w_j^2\right]+\gamma T\\ ={\sum }_{j=1}^T\left[G_j{w}_j+\frac{1}{2}\left(H_j+\lambda \right)w_j^2\right]+\gamma T\end{array}$

取最小值

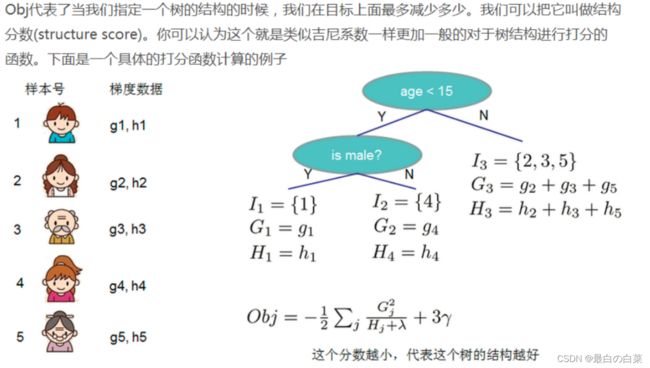
$\begin{array}{l}\frac{\partial J\left(f_t\right)}{\partial w_j}=G_j+\left(H_j+\lambda \right)w_j=0\\ w_j=-\frac{G_j}{H_j+\lambda }\\ Obj=-\frac{1}{2}{\sum }_{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T\end{array}$ 带回原目标函数

安装xgboost

记录下自己的一种超简单实用的安装流程。

进入：https://www.lfd.uci.edu/~gohlke/pythonlibs/#xgboost

我选的是这个xgboost-1.5.1-cp37-cp37m-win_amd64.whl(cp37指的是我python版本是3.7，根据版本选择)，然后需要启动CMD，切换目录到C:\Users\LH\Anaconda3\myLib（文件安装目录，根据自己下载的位置进行更改），在输入 pip install xgboost-1.5.1-cp37-cp37m-win_amd64.whl。

实战演示

import xgboost

# First XGBoost model for Pima Indians dataset
from numpy import loadtxt
from xgboost import XGBClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# load data
dataset = loadtxt('pima-indians-diabetes.csv', delimiter=",")
# split data into X and y
X = dataset[:,0:8]
Y = dataset[:,8]
# split data into train and test sets
seed = 7
test_size = 0.33
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=test_size, random_state=seed)
# fit model no training data
model = XGBClassifier()
model.fit(X_train, y_train)
# make predictions for test data
y_pred = model.predict(X_test)
predictions = [round(value) for value in y_pred]
# evaluate predictions
accuracy = accuracy_score(y_test, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))

Accuracy: 74.02%

from numpy import loadtxt
from xgboost import XGBClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# load data
dataset = loadtxt('pima-indians-diabetes.csv', delimiter=",")
# split data into X and y
X = dataset[:,0:8]
Y = dataset[:,8]
# split data into train and test sets
seed = 7
test_size = 0.33
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=test_size, random_state=seed)
# fit model no training data
model = XGBClassifier()
eval_set = [(X_test, y_test)]
model.fit(X_train, y_train, early_stopping_rounds=10, eval_metric="logloss", eval_set=eval_set, verbose=True)
# make predictions for test data
y_pred = model.predict(X_test)
predictions = [round(value) for value in y_pred]
# evaluate predictions
accuracy = accuracy_score(y_test, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))

[0] validation_0-logloss:0.60491
[1] validation_0-logloss:0.55934
[2] validation_0-logloss:0.53068
[3] validation_0-logloss:0.51795
[4] validation_0-logloss:0.51153
[5] validation_0-logloss:0.50935
[6] validation_0-logloss:0.50818
[7] validation_0-logloss:0.51097
[8] validation_0-logloss:0.51760
[9] validation_0-logloss:0.51912
[10] validation_0-logloss:0.52503
[11] validation_0-logloss:0.52697
[12] validation_0-logloss:0.53335
[13] validation_0-logloss:0.53905
[14] validation_0-logloss:0.54546
[15] validation_0-logloss:0.54613
[16] validation_0-logloss:0.54982
Accuracy: 74.41%

from numpy import loadtxt
from xgboost import XGBClassifier
from xgboost import plot_importance
from matplotlib import pyplot
# load data
dataset = loadtxt('pima-indians-diabetes.csv', delimiter=",")
# split data into X and y
X = dataset[:,0:8]
y = dataset[:,8]
# fit model no training data
model = XGBClassifier()
model.fit(X, y)
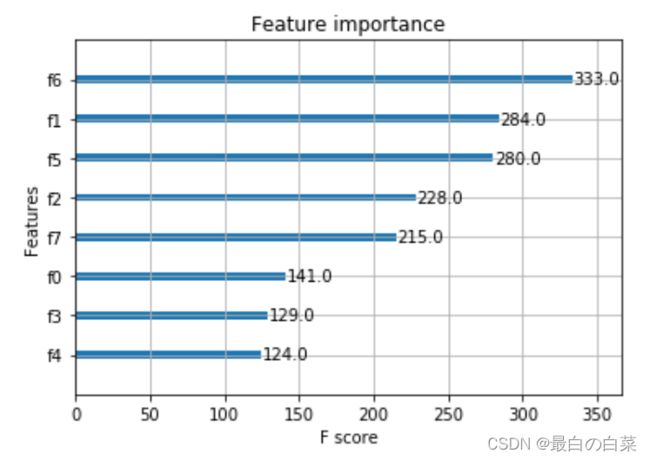
# plot feature importance
plot_importance(model)
pyplot.show()

# Tune learning_rate
from numpy import loadtxt
from xgboost import XGBClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import StratifiedKFold
# load data
dataset = loadtxt('pima-indians-diabetes.csv', delimiter=",")
# split data into X and y
X = dataset[:,0:8]
Y = dataset[:,8]
# grid search
model = XGBClassifier()
learning_rate = [0.0001, 0.001, 0.01, 0.1, 0.2, 0.3]
param_grid = dict(learning_rate=learning_rate)
kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=7)
grid_search = GridSearchCV(model, param_grid, scoring="neg_log_loss", n_jobs=-1, cv=kfold)
grid_result = grid_search.fit(X, Y)
# summarize results
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
means = grid_result.cv_results_['mean_test_score']
params = grid_result.cv_results_['params']
for mean, param in zip(means, params):
    print("%f  with: %r" % (mean, param))

Best: -0.530152 using {‘learning_rate’: 0.01}
-0.689563 with: {‘learning_rate’: 0.0001}
-0.660868 with: {‘learning_rate’: 0.001}
-0.530152 with: {‘learning_rate’: 0.01}
-0.552723 with: {‘learning_rate’: 0.1}
-0.653341 with: {‘learning_rate’: 0.2}
-0.718789 with: {‘learning_rate’: 0.3}

参数调节

1.learning rate

2.tree
max_depth
min_child_weight
subsample, colsample_bytree
gamma

3.正则化参数
lambda
alpha

xgb1 = XGBClassifier(
 learning_rate =0.1,
 n_estimators=1000,
 max_depth=5,
 min_child_weight=1,
 gamma=0,
 subsample=0.8,
 colsample_bytree=0.8,
 objective= 'binary:logistic',
 nthread=4,
 scale_pos_weight=1,
 seed=27)