Tensorflow导数梯度相关
导数与梯度
不知道的同学可以再回去看看数学,其实数学还是很有用的。
在高中阶段,我们就接触到导数(Derivative)的概念,它被定义为自变量产生一个微小 扰动∆后,函数输出值的增量∆与自变量增量∆的比值在∆趋于 0 时的极限。
导数本身没有方向,偏导数本身也没有方向。
考虑本质上为多元函数的神经网络模型,比如 shape 为[784, 256]的权值矩阵,它包 含了784 × 256个连接权值,我们需要求出784 × 256个偏导数。需要注意的是,在数学 表达习惯中,一般要讨论的自变量记为,但是在神经网络中,一般用来表示输入,比如 图片、文本、语音数据等,网络的自变量是网络参数集 = {1, 1, 2, 2, ⋯ }。利用梯度下 降算法优化网络时,需要求出网络的所有偏导数。因此,我们关心的也是误差函数输出L 沿着自变量方向上的导数,即L对网络参数的偏导数。
梯度的方向表示函数值上升最快的方向,梯度的反向则表示函数值下降最快的方向。
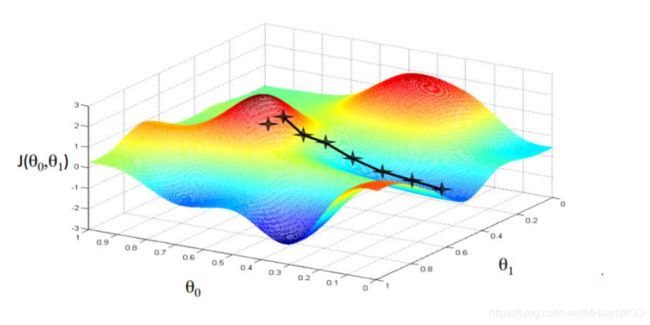
通过梯度下降算法并不能保证得到全局最优解,这主要是目标函数的非凸性造成的。 考虑非凸函数,深蓝色区域为极小值区域,不同的优化轨迹可能得到不同的最优数 值解,这些数值解并不一定是全局最优解。
神经网络的模型表达式通常非常复杂,模型参数量可达千万、数亿级别,几乎所有的 神经网络的优化问题都是依赖于深度学习框架去自动计算网络参数的梯度,然后采用梯度 下降算法循环迭代优化网络的参数直至性能满足需求。深度学习这里主要依赖的就是反向传播算法和梯度下降算法。
常用导数性质大家可以参考数学。
损失函数梯度?
import tensorflow as tf
# 构建待优化变量
x = tf.constant(1.)
w1 = tf.constant(2.)
b1 = tf.constant(1.)
w2 = tf.constant(2.)
b2 = tf.constant(1.)
# 构建梯度记录器
with tf.GradientTape(persistent=True) as tape:
# 非 tf.Variable 类型的张量需要人为设置记录梯度信息
tape.watch([w1, b1, w2, b2])
# 构建2层线性网络
y1 = x * w1 + b1
y2 = y1 * w2 + b2
dy2_dy1 = tape.gradient(y2, [y1])[0]
dy1_dw1 = tape.gradient(y1, [w1])[0]
dy2_dw1 = tape.gradient(y2, [w1])[0]不同的初始状态对梯度下降算法有影响
全连接层、激活函数层、池化层、卷积层、循环神经网络层层类,只需要在创建时指定网络层的相关参数,并调用__call__方法即可完成前向计算。在 调用__call__方法时,Keras 会自动调用每个层的前向传播逻辑,这些逻辑一般实现在类的 call 函数中。
网络容器
对于常见的网络,需要手动调用每一层的类实例完成前向传播运算,当网络层数变得 较深时,这一部分代码显得非常臃肿。可以通过 Keras 提供的网络容器 Sequential 将多个 网络层封装成一个大网络模型,只需要调用网络模型的实例一次即可完成数据从第一层到 最末层的顺序传播运算。
在完成网络创建 时,网络层类并没有创建内部权值张量等成员变量,此时通过调用类的 build 方法并指定 输入大小,即可自动创建所有层的内部张量。通过 summary()函数可以方便打印出网络结 构和参数量。
可以看到 Layer 列为每层的名字,这个名字由 TensorFlow 内部维护,与 Python 的对象名并 不一样。Param#列为层的参数个数,Total params 项统计出了总的参数量,Trainable params 为总的待优化参数量,Non-trainable params 为总的不需要优化的参数量。读者可以简单验 证一下参数量的计算结果。
当我们通过 Sequential 容量封装多个网络层时,每层的参数列表将会自动并入 Sequential 容器的参数列表中,不需要人为合并网络参数列表,这也是 Sequential 容器的便 捷之处。Sequential 对象的 trainable_variables 和 variables 包含了所有层的待优化张量列表 和全部张量列表
# 打印网络的待优化参数名与shape
for p in model.trainable_variables:
print(p.name, p.shape) # 参数名和形状
dense_3/kernel:0 (9, 64)
dense_3/bias:0 (64,)
dense_4/kernel:0 (64, 64)
dense_4/bias:0 (64,)
dense_5/kernel:0 (64, 1)
dense_5/bias:0 (1,)在训练网络时,一般的流程是通过前向计算获得网络的输出值,再通过损失函数计算 网络误差,然后通过自动求导工具计算梯度并更新,同时间隔性地测试网络的性能。对于 这种常用的训练逻辑,可以直接通过 Keras 提供的模型装配与训练等高层接口实现,简洁 清晰。
在 Keras 中,有 2 个比较特殊的类:keras.Model 和 keras.layers.Layer 类。其中 Layer 类是网络层的母类,定义了网络层的一些常见功能,如添加权值、管理权值列表等。 Model 类是网络的母类,除了具有 Layer 类的功能,还添加了保存模型、加载模型、训练 与测试模型等便捷功能。Sequential 也是 Model 的子类,因此具有 Model 类的所有功能。
损失函数也有模块:
# 导入优化器,损失函数模块
from tensorflow.keras import optimizers,losses
# 模型装配
# 采用Adam优化器,学习率为0.01;采用交叉熵损失函数,包含Softmax network.compile(optimizer=optimizers.Adam(lr=0.01),
loss=losses.CategoricalCrossentropy(from_logits=True),
metrics=['accuracy'] # 设置测量指标为准确率
)模型训练
模型装配完成后,即可通过 fit()函数送入待训练的数据集和验证用的数据集,这一步
称为模型训练。例如:
# 指定训练集为train_db,验证集为val_db,训练5个epochs,每2个epoch验证一次 # 返回训练轨迹信息保存在history对象中
history = network.fit(train_db, epochs=5, validation_data=val_db, validation_freq=2)
history.history
第八章好好看一下