不再简单地将频率当作概率
已知朴素贝叶斯公式:
P(C|F1,F2,…,Fn)=1ZP(C)∏ni=1P(Fi|C)
其中,Fi 表示样本的第 i 个特征,C 为类别标签。P(Fi|C) 表示样本被判定为类别 C 前提下,第 i个特征的条件概率。
之前,对于 P(Fi|C) 我们用频率来作为概率的估计,就如同上面例子中做的那样。
现在我们要采用另外一种方式,通过该特征在数据样本中的分布来计算该特征的条件概率。
首先先明确一下符号:
- D:表示训练集;
- Dc:表示训练集中最终分类结果为 c 的那部分样本的集合;
- X:表示一个训练样本(单个样本);
- x(j)i:表示第 j 个样本的第 i 个特征的特征值;
- m:D 中样本的个数;
- mc:Dc 中样本的个数,一般情况下(mc
我们假设:
P(xi|c) 具有特定的形式,这个具体的形式是事先就已经认定的,不需要求取。
P(xi|c) 被参数 θc,i 唯一确定。
那么,我们现在所拥有的是:
- P(xi|c) 的形式。
- 数据集合 D,其中每个样本的第 i 个特征都符合上述假定。
我们要做的是:利用 D 求出 θc,i 的值。
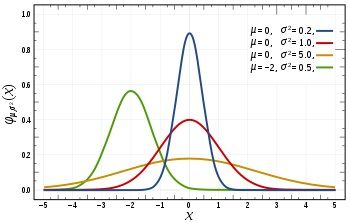
这里举例说明一下,比如:P(xi|c) 符合高斯分布,则:
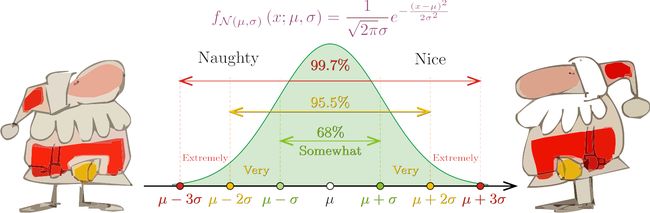
P(xi|c)=1√2πσ2c,iexp(−(xi−μc,i)22σ2c,i)
我们知道,高斯分布又名正态分布(在二维空间内形成钟形曲线),每一个高斯分布由两个参数——均值和方差,即上式中的 μc,i 和 σc,i ——决定,也就是说 θc,i=(μc,i,σc,i)。
如果我们认定特征 xi 具有高斯分布的形式,又知道了 μc,i 和 σc,i 的取值,我们也就获得了对应 xi 的具体概率分布函数。
直接带入 xi 的值计算相应条件概率,再进一步计算所有特征条件概率的积,就可以得出当前样本的后验概率了。
问题就在于:我们不知道 θc,i (μc,i 和 σc,i)的值,因此首先需要求出它们。
θc,i 是我们要以 D 为训练数据,通过训练过程得到的结果。
这个训练过程,要用到概率统计中参数估计(Parameter Estimation)的方法。
两个学派
注意: 这里插入一个有趣的小知识,如果不感兴趣,可以直接跳过本节!
统计学界有两个学派——频率学派(Frequentist)和贝叶斯学派(Bayesian)。这两个派系对于最基本的问题——世界的本质是什么样的——看法不同。
频率学派认为:世界是确定的,有一个本体,这个本体的真值不变。我们的目标就是要找到这个真值或真值所在的范围。
具体到“求正态分布的参数值”的问题,他们认为:这两个参数虽然未知,但是在客观上存在固定值,我们要做的是通过某种准则,根据观察数据(训练数据)把这些参数值确定下来。
贝叶斯学派认为:世界是不确定的,本体没有确定真值,而是其真值符合一个概率分布。我们的目标是找到最优的,可以用来描述本体的概率分布。
具体到“求正态分布的参数值”的问题,他们认为:这两个参数(均值和方差),本身也是变量,也符合某个分布。因此,可以假定参数服从一个先验分布,然后再基于观察数据(训练数据)来计算参数的后验分布。
本文我们讲的是朴素贝叶斯模型,那到了需要估计条件概率参数的时候,肯定是用贝叶斯学派的方法咯?还真不是!
这里,让我们来见识一下最常用的参数估计方法:频率学派的极大似然估计(Maximum Likelihood Estimation, MLE)。
具体讲解之前,我们先整理一下——
我们在学习的是朴素贝叶斯分类器,它是一个分类模型,它的模型函数是朴素贝叶斯公式——贝叶斯定理在所有特征全部独立情况下的特例。
贝叶斯定理的名称来自于18世纪的英国数学家托马斯 · 贝叶斯,因为他证明了贝叶斯定理的一个特例。
托马斯 · 贝叶斯 (1701 – 1761)
还有一群统计学家自称“贝叶斯学派”,因为他们认为世界是不确定的,这一点和他们的同行冤家“频率学派”正好相反。
在估计概率分布参数这件事情上,贝叶斯学派和频率学派各自有一套符合自身对世界设想的参数估计方法。
在构造朴素贝叶斯分类器的过程中,当遇到需要求取特征的条件概率分布的时候,我们需要估计该特征对应的条件概率分布的参数。
这时,通常情况下,我们会选用频率学派的做法——极大似然估计法。
下面要介绍的,也就是这种方法。
极大似然估计 (Maximum Likelihood Estimation, MLE)
参数估计的常用策略是:
- 先假定样本特征具备某种特定的概率分布形式;
- 再基于训练样本对特征的概率分布参数进行估计。
Dc 是训练集中所有被分类为 c 的样本的集合,其中样本数量为 mc;每一个样本都有 n 个特征;每一个特征有一个对应的取值。我们将第 j 个样本的第 i 个特征值记作:x(j)i。
我们已经假设 P(xi|c) 符合某一种形式的分布,该分布被参数 θc,i 唯一确定。为了明确起见,我们把 P(xi|c) 写作 P(xi|θc,i)。现在,我们要做的是,利用 Dc 来估计参数 θc,i。
现在我们要引入一个新的概念——似然(Likelihood)。似然指某种事件发生的可能,和概率相似。
二者区别在于:概率用在已知参数的情况下,用来预测后续观测所得到的结果。似然则正相反,用于参数未知,但某些观测所得结果已知的情况,用来对参数进行估计。
参数 θc,i 的似然函数记作 L(θc,i),它表示了 Dc 中的 mc 个样本 X1,X2,…Xmc 在第 i 个特征上的联合概率分布:
L(θc,i)=∏mcj=1P(x(j)i|θc,i)
极大似然估计,就是去寻找让似然函数 L(θc,i) 的取值达到最大的参数值的估计方法。
我们把让 L(θc,i) 达到最大的参数值记作 θ∗c,i。则 θ∗c,i 满足这样的情况:
将 θ∗c,i 带入到 P(xi|c) 的分布形式中去,确定了唯一的一个分布函数 f(x) (比如这个 f(x) 是一个高斯函数,θ∗c,i 对应的是它的均值和方差);
将 Dc 中每一个样本的第 i 个特征的值带入到 f(x) 中,得到的结果是一个 [0,1] 之间的概率值,将所有 mc 个 f(x) 的计算结果累计相乘,最后得出的结果是最大的。
也就是说将参数换成其他任何值,再做上述 1 和 2 之后的结果,一定小于 θ∗c,i 做 1 和 2 的结果。
说了这么多,我们到底要怎么求取 θ∗c,i 呢?
求取 θ∗c,i 的过程,就是最大化 L(θc,i) 的过程:
θ∗c,i=argmaxL(θc,i)
怎么才能最大化 L(θc,i) 呢?
为了便于计算,我们对上面等式取对数,得到 θc,i 的对数似然:
LL(θc,i)=∑mcj=1log(P(x(j)i|θc,i))
要知道,最大化一个似然函数同最大化它的自然对数是等价的。
因为自然对数 log 是一个连续且在似然函数的值域内严格递增的上凸函数。所以我们可以参考前面线性回归目标函数的求解办法:对似然函数求导,然后在设定导函数为0的情况下,求取 θc,i 的最大值——θ∗c,i
正态分布的极大似然估计
下面来看一个具体的例子——P(xi|c) 为正态分布。此时,我们有:
LL(θc,i)=LL(μc,i,σ2c,i)=∑mcj=1log(1√2πσ2c,iexp(−(x(j)i−μc,i)22σ2c,i))
注意,这里我们把 σ2c,i 看作一个独立参数,即:
θc,i=(μc,i,σ2c,i)
我们先对 μc,i 求偏导:
∂LL(μc,i,σ2c,i)∂μc,i=∑mcj=1(x(j)i−μc,iσ2c,i)
令: ∂LL(μc,i,σ2c,i)∂μc,i=0
则: ∑mcj=1(x(j)i−μc,iσ2c,i)=0
有: μc,i=1mc∑mcj=1(x(j)i)
然后对 σc,i 求偏导:
∂LL(μc,i,σ2c,i)∂σ2c,i=∑mcj=1(−12σ2c,i+(x(j)i−μc,i)22σ2c,iσ2c,i)
令: ∑mcj=1(−12σ2c,i+(x(j)i−μc,i)22σ2c,iσ2c,i)=0
最后得出:
σ2c,i=1mc∑mcj=1(x(j)i−μc,i)2
这样我们就估算出了第 i 个特征正态分布的两个参数,第 i 个特征的具体分布也就确定下来了。
注意:虽然我们此处用的是正态分布——一种连续分布,但是实际上,离散特征的分布一样可以用同样的方法来求,只不过把高斯分布公式改成其他的分布公式就好了。
估算出了每一个特征的 θc,i 之后,再将所有求出了具体参数的分布带回到朴素贝叶斯公式中,生成朴素贝叶斯分类器,再用来做预测,就好了。
用代码实现朴素贝叶斯模型
上文中例子4用代码来实现,如下所示:
下列数据直接存储为 career_data.csv 文件:
no,985,education,skill,enrolled
1,Yes,bachlor,C++,No
2,Yes,bachlor,Java,Yes
3,No,master,Java,Yes
4,No,master,C++,No
5,Yes,bachlor,Java,Yes
6,No,master,C++,No
7,Yes,master,Java,Yes
8,Yes,phd,C++,Yes
9,No,phd,Java,Yes
10,No,bachlor,Java,No
数据和脚本放在统一路径下,运行脚本,输出如下:
Number of mislabeled points out of a total 1 points : 0, performance 100.00%