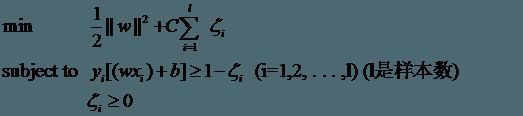本人水平有限,如果有错误的地方,希望各位大神能够不吝赐教,及时指正。
老规矩,喝水不忘掘井人,首先要感谢发明SVM算法的前辈Vapnik。其次,也要感谢Sean的引领,把我带入这一行,否则,光靠我自己摸索,会花去更多的时间、精力。最后,要感谢无数的人,那些对我的思考方式产生影响的人。
【我们生在一个不算太坏的时代,Vapnik前辈刚刚提出SVM算法的时候,局限于那个年代计算机计算能力的不足,根本没有多少人重视SVM算法。】
又是一次喜忧参半,喜的是,技多不压身,又多了一个解决问题的手段,忧的是,这个手段....好像也不能指望其预测股价啊。
SVM算法的推导过程中,将使用到拉格朗日乘数,还有一些向量知识。SVM其实也是一种分类算法,当然了,分类算法可以有很多,不过,SVM确有其强大的地方。【较之于上一篇的神经网络,SVM是一个凸空间,所以不会存在局部极值的问题。】
【这里又要插句题外话,你们可能在其它某个地方,会看到“聚类”这个词,虽然只和“分类”差了一个字,但是在算法上,意义完全不同。假如,你看到一群人,如果我让你用肉眼去观察,超过178公分(为什么是178,因为Binhao的身高是178)的为一类人,不超过的为另一类人,那么,这个就叫分类。如果我不给定“178公分”这个指标或者说标签,让你把这些人归类,那你可能会这样做:自己衡量一个度,高的为一类,矮的为一类,或者以胖的-中等-瘦的归类,或者戴不戴眼镜、头发长中短、肤色等等,所有这些,我都没有指定某个指标或贴上某个标签,完全是你根据这群人当中每个人的特点,来自己归类,这个就叫聚类。所以也可以看出,分类是有监督的,聚类是无监督的。】
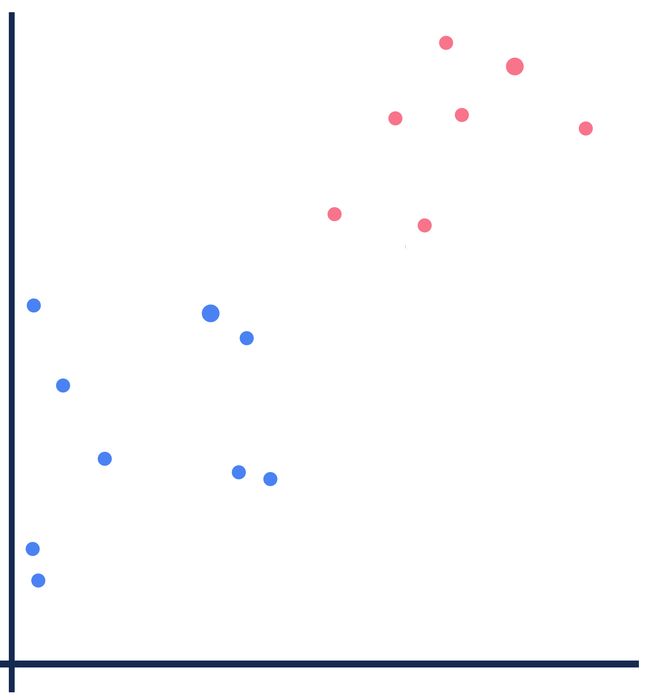
来看这样一副图:
如果要把图中的红点和蓝点,用界线区分开,那不同的分类算法划出来的线可能会不同:
绿色的界线可能来自神经网络,黄色的界线可能来自决策树,紫色的界线就是单纯的一条直线,也可能是来自KNN(最近邻居算法)。
然而,虽然我画图不怎么样,但是审美还是可以的,而且估计强迫症犯了,总觉得这些线条都不太完美。但是我一下子又想不出来更完美的线条。大自然是神奇而美妙的,它给了我们无数的馈宝。于是,我夜观天象,(我们应该致力于环境的保护,不然晚上看到的天空都是灰蒙蒙一片。但愿AI能够在环保也做出巨大贡献。)无意之中,神奇而美妙的星空,给了我灵感。如果我把图-1稍加修饰一下:
我把图-1中的蓝点用蓝线连了起来,红点用红线连了起来,这看起来像什么?蓝色的点阵就好像夜空中的天鹰座,红色的点阵就好像夜空中的天琴座。你不太知道这两个星座没关系,不过你一定听说过,牛郎星和织女星。仔细再看一下,最大的那颗蓝色的点就是牛郎星,最大的那颗红色的点就是织女星。
虽然我肉眼无法观测到银河,但是我可以想到,把天鹰座和天琴座隔开的,是银河。所以,又可以改动下图片:
我们知道,在天文学角度,牛郎星和织女星是不可能碰到一块的。但是在我国的古典文学典故里,为了分开牛郎和织女,这条银河被设计为尽可能最宽。
感谢大自然,感谢宇宙,这些灵感很重要。接下去,就该把这副图交给拥有七十二般变化的数学了。
SVM:Support Vector Machine,支持向量机。图-4虚线经过的点,如果把它们看作是一个个向量的坐标的话,这些坐标将有助于确定一个几何空间中的超平面,这个超平面用来区分这些数据,所以称之为支持向量,那么“机”呢?我不知道,我真的不知道。但Sean说得是对的,就是算法的意思。汉语里,我们会说,“我写了一套【代码\程序\软件\系统】”,很多时候,中括号里的四个词都是可以互换的,细微的差别只在于听的人感受到的高大上的程度不同而已,所以,英语里“Learning、Machine、Algorithm”也是同一个道理。
那么我们来看看,向量究竟能帮助我们解决那些困惑:
(这些直线都不太直,希望你们能体谅一下。)
假设,有向量w,对向量w暂且只有一个要求,在方向上,它垂直于作为分割的那条实线。同时,我们知道,银河之中还有很多星星点点,分布于实线两侧、虚线之内,假设其中就有一点x,我们看作向量x。
因为w是垂直于实线的,所以向量x在w上的投影,如下图所示:
黄色线条即为x在w上的投影,记为wx【老规矩,键盘输入限制,也是为了节省时间,箭头就不画了,但这里实际表示的是向量】。
如果这条黄色投影的长度越过了实线,也就是超过了某个长度,我们认为它就是一类(或者说正例),记为 wx - c >=0,反之,就是另一类(反例),记为 wx - c <0。
多么熟悉的片段,故伎重演,令c = -b,则有:wx + b >0 和 wx +b <0。
到这里还没有完,因为x是在两条虚线内的,我们现在是要对两条虚线外的点进行分类,所以我们不得不再次使用数学上的便利。
假设有一个正例的x(右侧虚线外),则我们要求 wx + b >= 1,对于反例的x(左侧虚线外),则 wx + b <= -1。【注意,这一行的x只是名字上和上面几行的x一样,代表的意义已经不同。这正是之前提到的,不要被公式的不同表达形式给蒙蔽。】
再假设有一个变量y,当wx + b >= 1时,y等于1;当wx + b <= -1时,y等于-1。
在等式两边都乘以y,对于正例的x,有:y(wx + b) >= 1;对于反例的x,也有:y(wx + b) >= 1 【wx + b <= -1的两边同时乘以了值为-1的y】。
y(wx + b) >=1,即y(wx + b) - 1 >= 0。
但我现在要让y(wx + b) - 1 = 0,等于0在图像上意味着,在那两条虚线上。
在我国古典文学典故里,七夕是牛郎织女相会的日子。现在假设在七夕那天,织女来到银河边,牛郎早就已经等在银河的那边了。因为银河被设计为尽可能宽,所以,接下来,在喜鹊搭建鹊桥的时候,数学是否能够帮助我们计算出这个最大宽度呢?
由图可知,向量z代表织女星,向量n代表牛郎星,两点之间的直线距离为:向量z-向量n,记作(z-n)【箭头省略了,你们懂的】。
w是条垂直于直线的向量。所以,河的宽度为:(z-n)w / ‖w‖。
虽然这里n代表了牛郎星,z代表了织女星,但是往上翻一翻,n其实就是之前“反例的x”,z就是“正例的x”。由y(wx+b) -1 = 0以及正反例下y的取值(-1,1),可得:nw = -b - 1, zw = -b + 1。所以:(z-n)w / ‖w‖ = [-b + 1 - (-b - 1)] / ‖w‖ = 2 / ‖w‖。
现在要求河的宽度( 2 / ‖w‖)的最大值,也就是求‖w‖的最小值,又是老生常谈了,也就是求1/2 * ‖w‖^2的最小值。
但是,这次的求极值,与以往有些不一样。因为:1/2 * ‖w‖^2是有约束条件的,w必须满足y(wx+b) -1 = 0。在带有约束条件的函数求极值的情况下,我们要引入拉格朗日乘数,从而摆脱约束条件的束缚。
我们用R表示河宽:【要求极值的函数 - 总和(拉格朗日乘子 * 约束条件函数)】
R = 1/2 * ‖w‖^2 - ∑λ[y(wx + b) - 1]
= 1/2 * ‖w‖^2 - (∑λywx + ∑λyb - ∑λ) 【敲黑板,w,x是向量,原因你们懂的】
接下去又回到熟悉的套路了,对w求偏导,并令偏导函数结果为0:
ΔR/Δw = w - ∑λyx = 0【上一篇提到的,对w求偏导,就把除w以外的皆看作常数,常数的导数为零,再配合函数加法及乘法求导规则】
所以 w = ∑λyx。
对b求偏导:
ΔR/Δb = ∑λy = 0,所以,∑λy = 0。
再把 w = ∑λyx 代入R,得:
R = 1/2 * (∑λyx)(∑λyx) - (∑λyx)(∑λyx) - b∑λy + ∑λ,代入∑λy = 0,得:
R = ∑λ - 1/2 (∑λyx)(∑λyx) = ∑λ - 1/2 ∑∑λλyyxx 【两个样本点积】
河的最大宽度取决于两个样本的点积。
于是就有:wx + b = (∑λyx)x + b(也取决于两个样本间的点积)
这两个式子(河宽与虚线)都与样本的线性和有关联。我们来反思一下,我们为什么要引入拉格朗日乘数?因为要求河宽的极值。河宽边界上有什么?支持向量,因为落在边界(虚线)上的的向量可以确定一个超平面,所以叫支持向量。那也就是说,拉格朗日乘数只参与到支持向量的确认中,如果某个向量不是支持向量,那么拉格朗日乘数就对它没有效果,也就是λ=0。而非支持向量的数量一般来说,总是多于支持向量,所以在∑λyx中,很多项都为0。
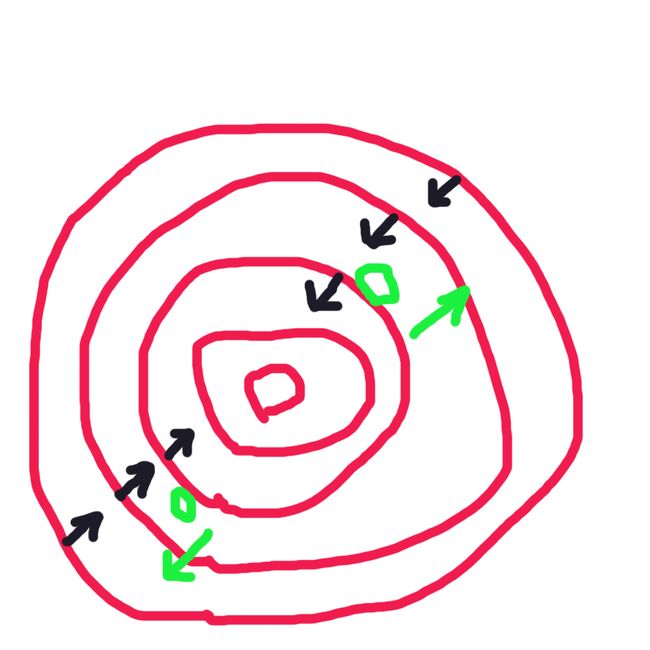
【本段粗斜体部分,包括图-12,为今早追加部分。是昨晚入睡时,突然顿悟Sean曾经举例过的两个圆相切的例子。但愿你们还记得上一篇神经网络提到的等高线图,不同的是,上一回是用来爬山,所以越里面的圆,高度越高,这一回,1/2 * ‖w‖^2是个多维空间的凸空间(图-12红圈部分),所以又回到了梯度下降,即越往里面,高度越低。为了简化形式,令f(w) = 1/2 * ‖w‖^2;g(w) = y(wx + b) - 1 = 0(河的边界,也就是那两条虚线)。由已知情况可得,f(w)是在朝里移动,f(w)朝里意味着河的边界在扩大,也就是g(w)在朝外侧移动(图-12绿圈部分),当f(w)与g(w)外切时,这一切点上,它们两个方向相反,大小不等。所以要令f(w) = λg(w),这样,f(w)的导数 = λg(w) 的导数,推得:f(w)的导数 - λg(w) 的导数 = 0,也就是 (f(w) - λg(w))的导数 = 0,就是再上面的一大串公式推导了。从图里也能看出,λ大于等于0,而且它不是对所有的满足f(w)的w有约束。】
当然,如果遇到噪音,或者一些脱离群体的数据,比方说,图-7中的织女星z,如果通过鹊桥来到银河对岸,那么这个时候,银河就不能把她和牛郎星分开,即“线性不可分”【图-8】
这个时候,我们引入松弛变量,希腊字母'ζ',以及惩罚因子,C,放弃这类点。
【C是事先我们自行指定的值,可以调整。】
如果仅仅是平面线性分类,那似乎SVM也没有体现出多少强大,反而展现了其计算复杂的一面。我们古人怎么形容一个人的能力的,如果要表示一个人的能力非常非常非常非常厉害?
“斗转星移、扭转乾坤、神鬼莫测、夺天地造化 ....”。假设出现了这样一种能力,宇宙空间被改变了,天鹰座和天琴座拟合到一块去了,见图-10:
显然,这是线性不可分的。
“天地之初,一片混沌,盘古一划,开天辟地。”
还记得上一篇提到的等高线图么?假设图-10也是俯瞰所得,现在,你跑到平地,从侧面正视,应该就是图-11的样子:
“盘古一划,开天辟地”,从平面的线性不可分,被拔高到多维平面的可分。这个时候再回过头去看图-10,你脑海里会自动绘制一条曲线来分割不同色彩的点。手中无剑,心中有剑,这就是一个看山是山-看山不是山-看山是山的过程。
以上大部分都是文学修辞色彩,在数学上,我们继续引入其它功能:核函数。
【我曾询问过Sean,核函数可不可以我们自己写一个,Sean说可以,但是要遵循Mercer定理,我去简单查了查Mercer定理,意识到这是一个关于矩阵的“深渊”,我决定暂时先不往里跳了。】
很明显,从图-10的二维平面,到图-11的多维平面,向量的坐标被变化了,假设变化后的x为:
change(x),我们已经知道,最大宽度与边界只与样本间的点积有关(change(x1) change(x2)),所以,核函数的功能就是为了计算出变化后的样本向量的点积。
假设核函数K,那么有:K(x1, x2) = change(x1) change(x2) 【鉴于键盘输入限制,也为了节省时间,向量的箭头省略了。】
那我们可以采用哪些现有的核函数K呢?
e^(- ‖x1-x2‖ / σ)
【看到这个函数,我们应该能自然联想到,它可能会导致过拟合。】
还是那句话,没有哪个算法是万能的,关键还是在于把实际问题抽象到输入向量。
本人水平有限,如果有错误的地方,希望各位大神能够不吝赐教,及时指正。
抛了两块砖了,写得不好,望轻拍。