leetcode排序算法-学习笔记
文章目录
- 1简介
-
- 稳定性:
- 就地性:
- 自适应性:
- 2冒泡算法
-
- 2.1算法简介
- 2.2效率优化
- 3 快速排序
-
- 3.1 算法解析
- 3.2算法特性
- 3.3 算法优化
-
- Tail Call :
- 随机基准数:
- practise
-
- 剑之40 最小k个数
-
- 冒泡算法--超出时间限制
- 快速排序
1简介
稳定性:
根据 相等元素 在数组中的 相对顺序 是否被改变,排序算法可分为「稳定排序」和「非稳定排序」两类。
- 「稳定排序」在完成排序后,不改变 相等元素在数组中的相对顺序。例如:冒泡排序、插入排序、归并排序、基数排序、桶排序。
- 「非稳定排序」在完成排序后,相等素在数组中的相对位置 可能被改变。例如:选择排序、快速排序、堆排序。
就地性:
根据排序过程中 是否使用额外内存(辅助数组),排序算法可分为「原地排序」和「异地排序」两类。一般地,由于不使用外部内存,原地排序相比非原地排序的执行效率更高。
- 原地排序,不使用额外辅助数组,例如:冒泡排序、插入排序、选择排序、快速排序、堆排序。
- 非原地排序,使用额外辅助数组,例如:归并排序、基数排序、桶排序。
自适应性:
根据算法 时间复杂度 是否 受待排序数组的元素分布影响 ,排序算法可分为「自适应排序」和「非自适应排序」两类。
- 自适应排序的时间复杂度受元素分布影响;例如:冒泡排序、插入排序、快速排序、桶排序。
- 非自适应排序的时间复杂度恒定;例如:选择排序、归并排序、堆排序、基数排序。
2冒泡算法
2.1算法简介
冒泡排序是最基础的排序算法,由于其直观性,经常作为首个介绍的排序算法。其原理为:
内循环: 使用相邻双指针 j , j + 1 从左至右遍历,依次比较相邻元素大小,若左元素大于右元素则将它们交换;遍历完成时,最大元素会被交换至数组最右边 。
外循环: 不断重复「内循环」,每轮将当前最大元素交换至 剩余未排序数组最右边 ,直至所有元素都被交换至正确位置时结束
def bubble_sort(nums):
N = len(nums)
for i in range(N - 1): # 外循环
for j in range(N - i - 1): # 内循环
if nums[j] > nums[j + 1]:
# 交换 nums[j], nums[j + 1]
nums[j], nums[j + 1] = nums[j + 1], nums[j]
2.2效率优化
通过增加一个标志位 flag ,若在某轮「内循环」中未执行任何交换操作,则说明数组已经完成排序,直接返回结果即可。
优化后的冒泡排序的最差和平均时间复杂度仍为 O(N2) ;在输入数组已排序 时,达到最佳时间复杂度Ω(N) 。
def bubble_sort(nums):
N = len(nums)
for i in range(N - 1):
flag = False # 初始化标志位
for j in range(N - i - 1):
if nums[j] > nums[j + 1]:
nums[j], nums[j + 1] = nums[j + 1], nums[j]
flag = True # 记录交换元素
if not flag: break # 内循环未交换任何元素,则跳出
3 快速排序
3.1 算法解析
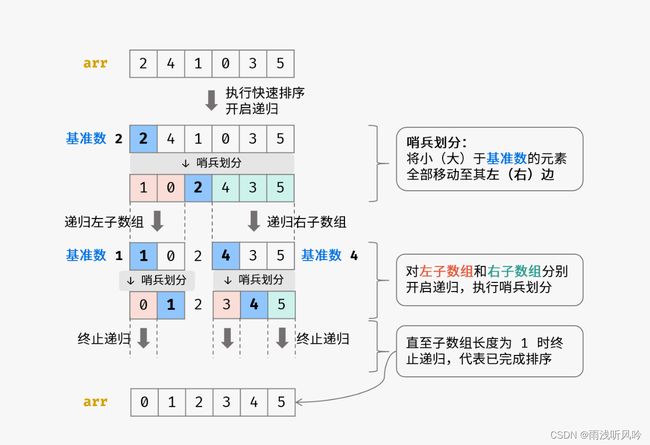
快速排序算法有两个核心点,分别为 哨兵划分 和 递归 。
- 哨兵划分:
以数组某个元素(一般选取首元素)为 基准数 ,将所有小于基准数的元素移动至其左边,大于基准数的元素移动至其右边。 - 递归:
对 左子数组 和 右子数组 分别递归执行 哨兵划分,直至子数组长度为 1 时终止递归,即可完成对整个数组的排序。
def quick_sort(nums, l, r):
# 子数组长度为 1 时终止递归
if l >= r: return
# 哨兵划分操作
i = partition(nums, l, r)
# 递归左(右)子数组执行哨兵划分
quick_sort(nums, l, i - 1)
quick_sort(nums, i + 1, r)
return nums
def partition(nums, l, r):
# 以 nums[l] 作为基准数
i, j = l, r
while i < j:
while i < j and nums[j] >= nums[l]: j -= 1
while i < j and nums[i] <= nums[l]: i += 1
nums[i], nums[j] = nums[j], nums[i]
nums[l], nums[i] = nums[i], nums[l]
return i
# 调用
nums = [3, 4, 1, 5, 2]
quick_sort(nums, 0, len(nums) - 1)
3.2算法特性
3.3 算法优化
快速排序的常见优化手段有「Tail Call」和「随机基准数」两种。
Tail Call :
由于普通快速排序每轮选取「子数组最左元素」作为「基准数」,因此在输入数组 完全倒序 时, partition() 的递归深度会达到 N ,即 最差空间复杂度 为 O(N) 。
每轮递归时,仅对 较短的子数组 执行哨兵划分 partition() ,就可将最差的递归深度控制在 O(logN)(每轮递归的子数组长度都 ≤当前数组长度 /2 ),即实现最差空间复杂度 O(logN)
def quick_sort(nums, l, r):
# 子数组长度为 1 时终止递归
while l < r:
# 哨兵划分操作
i = partition(nums, l, r)
# 仅递归至较短子数组,控制递归深度
if i - l < r - i:
quick_sort(nums, l, i - 1)
l = i + 1
else:
quick_sort(nums, i + 1, r)
r = i - 1
随机基准数:
同样地,由于快速排序每轮选取「子数组最左元素」作为「基准数」,因此在输入数组 完全有序 或 完全倒序 时, partition() 每轮只划分一个元素,达到最差时间复杂度 O(N2) 。
因此,可使用 随机函数 ,每轮在子数组中随机选择一个元素作为基准数,这样就可以极大概率避免以上劣化情况。
值得注意的是,由于仍然可能出现最差情况,因此快速排序的最差时间复杂度仍为 O(N2)。
def partition(nums, l, r):
# 在闭区间 [l, r] 随机选取任意索引,并与 nums[l] 交换
ra = random.randrange(l, r + 1)
nums[l], nums[ra] = nums[ra], nums[l]
# 以 nums[l] 作为基准数
i, j = l, r
while i < j:
while i < j and nums[j] >= nums[l]: j -= 1
while i < j and nums[i] <= nums[l]: i += 1
nums[i], nums[j] = nums[j], nums[i]
nums[l], nums[i] = nums[i], nums[l]
return i
practise
剑之40 最小k个数
冒泡算法–超出时间限制
class Solution:
def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
n=len(arr)
for i in range(n-1):
flag=False
for j in range(n-i-1):
if arr[j]>arr[j+1]:
arr[j],arr[j+1]=arr[j+1],arr[j]
flag=True
if flag==False:
break
return arr[:k]

上面代码已经是优化后的冒泡排序,但是优化后的冒泡排序的最差和平均时间复杂度仍为 O(N2);在输入数组 已排序 时,达到最佳时间复杂度 Ω(N)。
当然也可以用冒泡排序进一步优化,知识第一层循环不用len(arr)-1,而使用k,但仍然超时
正向
class Solution:
def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
n=len(arr)
for i in range(n-k):
flag=False
for j in range(n-i-1):
if arr[j]>arr[j+1]:
arr[j],arr[j+1]=arr[j+1],arr[j]
flag=True
if flag==False:
break
return arr[:k]
反向
class Solution:
def getLeastNumbers(self, arr, k):
n=len(arr)
for i in range(k):
for j in range(n-i-1):
if arr[-j-1]<arr[-j-2]:
arr[-j-1],arr[-j-2]=arr[-j-2],arr[-j-1]
return arr[:k]
快速排序
基础方法
使用常规快速排序效果一般
class Solution:
def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
self.quick_sort(arr,0,len(arr)-1)
return arr[:k]
def quick_sort(self,arr,l,r):
if l>=r:return
i=self.partition(arr,l,r)
self.quick_sort(arr,l,i-1)
self.quick_sort(arr,i+1,r)
#递归函数
def partition(self,arr,l,r):
i,j=l,r
while i<j:
while i<j and arr[j]>=arr[l]:
j-=1
while i<j and arr[i]<=arr[l]:
i+=1
arr[i],arr[j]=arr[j],arr[i]
arr[l],arr[i]=arr[i],arr[l]
return i
class Solution:
def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
self.quick_sort(arr,0,len(arr)-1,k)
return arr[:k]
def quick_sort(self,arr,l,r,k):
if l>=r:return
i=self.partition(arr,l,r)
if k<i:
return self.quick_sort(arr,l,i-1,k)
if k>i:
return self.quick_sort(arr,i+1,r,k)
#递归函数
def partition(self,arr,l,r):
i,j=l,r
while i<j:
while i<j and arr[j]>=arr[l]:
j-=1
while i<j and arr[i]<=arr[l]:
i+=1
arr[i],arr[j]=arr[j],arr[i]
arr[l],arr[i]=arr[i],arr[l]
return i
缩减代码如下,但是会超时
class Solution:
def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
n=len(arr)
def qucik_sort(l,r):
if l>=r :return
i,j=l,r
while i<j:
while i<j and arr[j]>=arr[l]:
j-=1
while i>j and arr[i]<=arr[l]:
i+=1
arr[i],arr[j]=arr[j],arr[i]
arr[l],arr[i]=arr[i],arr[l]
if k<i:
return qucik_sort(l,i-1)
if k>i:
return qucik_sort(i+1,r)
qucik_sort(0,n-1)
return arr[:k]