什么事数据结构?
数据结构是以某种特定的布局方式存储数据的容器。这种‘布局方式’决定了数据结构对于某些操作是高效的,而对于其他操作是低效的。首先我们需要理解各种数据结构,才能在实际处理问题时选择合适的数据结构。
下面我们重点分析一下常用的数据机构
- 数组
- 栈
- 队列
- 链表
- 树
- 图
- 字典树
- 散列表(哈希表)
一 数组
所谓数组 是有序的元素序列, 比如[1, 3, 4, 6] 数组长度为4,每个元素关联一个正数,我们称之为索引,它表明数组中每个元素所在的位置,大部分语言初始值索引定义为0
类型:
- 一维数组
- 多维数组
特点:
- 在内存中数组是一块连续的区域
- 数组需要预留空间,在使用前需要先申请内存的大小,可能会浪费内存空间
- 插入数据和删除数据效率低,插入数据时,这个位置后面的数据在内存中都要向后移。
- 随机读取效率很高。因为数组时连续的,知道每一个数据的内存地址,可以直接找到给地址的数据。
- 不利扩展,数组定义的空间不够时需要重新定义数组。
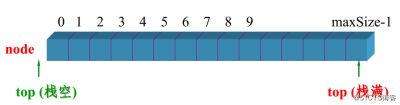
二 栈
著名的撤销操作几乎遍布任意一个应用。但是你有没有思考过他是如何工作的呢?这个问题的解决思路时按照将最后的状态排列在先的顺序 ,在内存中存储历史工作状态(当然,他会受限一定的数量),这没办法用数组实现,但有了栈,就变的非常方便了。
可以把栈想象成一列垂直堆放的书,为了拿到中间的书,你需要移除放置在这上面的所有的书,这是后进先出的工作原理。
特点:
- 数据的插入和删除只能通过一端实现,这一端称为栈顶,另一端栈底
实现:
栈的顺序存储和链式存储实际时栈的容器不同,一个数组实现 一个链表实现
-
顺序存储实现
//栈的顺序存储:用数组来存放元素:数组0端为栈底;length-1端为栈顶
public class MySqStack {
int[] data;//数组
int top;//数组的下标
public MySqStack(int size) {
data = new int[size];
top = -1;
}
// 进栈
public boolean push(int element) {
// 如果栈满,则不能插入
if (top == data.length - 1) {
// throw new RuntimeException("stack is empty");
return false;
} else {
top++;
data[top] = element;
return true;
}
}
// 出栈
public int pop() {
// 如果栈中没有元素
if (top == -1) {
throw new RuntimeException("stack is empty");
} else {
return data[top--];
}
}
// 取栈顶元素
public int GetTop() {
// 如果栈中没有元素
if (top == -1) {
throw new RuntimeException("stack is empty");
} else {
return data[top];
}
}
-
链式存储实现
public class LinkStack {
class Node {
int data;
Node next;
}
// 创建头节点
private Node header = new Node();
// 新节点进栈:头插入法:插入头节点之后
public boolean push(int data) {
Node node = new Node();
node.data = data;
node.next = header.next;
header.next = node;
return true;
}
//出栈:将头节点之后的节点出栈
public int pop() {
if(header.next == null) {
return -1;
}
else {
int rtn = 0;
rtn = header.next.data;
header.next = header.next.next;
return rtn;
}
}
//取栈顶元素
public int getTop() {
if(header.next == null) {
return -1;
}
else {
return header.next.data;
}
}
应用:
安卓activity页面栈管理
三 队列
定义:
与栈相似,队列是一种顺讯存储元素的线形数据结构。栈与队列的最大差别在于栈是LIFO(后进先出)而队列是FIFO(先进先出)
一个完美的队列实现例子:销售亭排队,如果有新的人加入,它需要到队尾去排队,而非队首------排在前面的人会先拿到票,然后离开队伍。
实现:
class Queue(object):
def __init__(self):
self.items = []
def enqueue(self,item):
self.items.insert(0,item)
def dequeue(self):
return self.items.pop()
def isEmpty(self):
return self.items==[]
def size(self):
return len(self.items)
应用:
约瑟夫环问题(Josephus problem):n个人围成一圈,从1开始报数,每当有人报到m时,他被淘汰,下一个人继续从1开始报数,问最后的获胜者是谁?
Hot potato game:N个人编号1~N,围坐成一个圆圈。从1号人开始传递一个热土豆,经过M次传递后拿着热土豆的人被清除离座,由坐在后面的人拿起热土豆继续进行游戏。最后剩下的人获胜.
上面两个问题相同,如果M=0和N=5,则游戏人依序被清除,5号游戏人获胜。如果M=1 和N=5,那么被清除的人的顺序是2,4,1,5,最后3号人获胜。
#n个人围成一圈,第一个人从1开始报数,每当有人报到m时,他被淘汰,下一个人继续从1开始报数
def josephus(people_list,num):
q = Queue()
for people in people_list:
q.enqueue(people)
while q.size()>1:
for i in range(num-1):
q.enqueue(q.dequeue())
q.dequeue()
return q.dequeue()
people_list = [1,2,3,4,5]
print josephus(people_list,7)
四 链表
定义:
链表是另一个重要的线性数据结构,乍一看可能有点像数组,但在内存分配、内部结构以及数据插入和删除的基本操作方面均有所不同。链表就像一个节点链,其中每个节点包含着数据和指向后续节点的指针。 链表还包含一个头指针,它指向链表的第一个元素,但当列表为空时,它指向null或无具体内容。
链表一般用于实现文件系统、哈希表和邻接表。
特点:
- 在内存中可以存在任何地方,不要求连续
- 每个数据保存下一个数据的内存地址,通过这个地址找到下一个数据。
- 增加数据和删除数据比较容易。
- 查找数据效率低,因为不具有随机访问醒,所以访问某个位置的数据都要从第一个数据开始访问,然后根据第一个数据保存的下一个数据的地址找到第二个数据,以此类推。(数组查找更快因为内存是连续的只要遍历地址就可以,可以直接找到对应地址的数据)
- 不指定大小,扩展方便。链表大小不用定义,数据随意增删
类型:
- 单链表
typedef struct node
{
int val;
struct node *next;
}Node;
- 双向链表
typedef struct node
{
int val;
struct node *pre;
struct node *next;
}Node;
应用:
经典的链表应用场景: LRU 缓存淘汰算法
缓存是一种提高数据读取性能的技术,在硬件设计、软件开发中都有着非常广泛的应用,比如常见的CPU缓存、数据库缓存、浏览器缓存等等。
缓存空间的大小有限,当缓存空间被用满时,哪些数据应该被清理出去,哪些数据应该被保留?这就需要缓存淘汰策略来决定。常见的缓存清理策略有三种:先进先出策略FIFO(First In, First Out)、最少使用策略 LFU(Least Frequently Used)、最近最少使用策略LRU(Least Recently Used)。
如何用链表来实现LRU缓存淘汰策略呢?
思路:
维护一个有序单链表,越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时,我们从链表头部开始顺序遍历链表,如果此数据之前已经被缓存在链表中了,我们遍历得到这个数据的对应结点,并将其从原来的位置删除,并插入到链表头部。如果此数据没在缓存链表中,又可以分为两种情况处理:
如果此时缓存未满,可直接在链表头部插入新节点存储此数据;
如果此时缓存已满,则删除链表尾部节点,再在链表头部插入新节点。
五 树
定义:
树形结构是一种非线形,层级式的数据结构,由顶点(节点)和连接它们的边组成。 树类似于图,但区分树和图的重要特征是树中不存在环路。
树形结构被广泛应用于人工智能和复杂算法,它可以提供解决问题的有效存储机制
二叉树
每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分,其次序不能任意颠倒。
B树
b树(balance tree)和b+树应用在数据库索引,可以认为是m叉的多路平衡查找树,但是从理论上讲,二叉树查找速度和比较次数都是最小的,为什么不用二叉树呢?
因为我们要考虑磁盘IO的影响,它相对于内存来说是很慢的。数据库索引是存储在磁盘上的,当数据量大时,就不能把整个索引全部加载到内存了,只能逐一加载每一个磁盘页(对应索引树的节点)。所以我们要减少IO次数,对于树来说,IO次数就是树的高度,而“矮胖”就是b树的特征之一,它的每个节点最多包含m个孩子,m称为b树的阶,m的大小取决于磁盘页的大小。
B+树
b+树,是b树的一种变体,也是一种多路搜索树,查询性能更好
B和B+树的区别在于,B+树的非叶子结点只包含导航信息,不包含实际的值,所有的叶子结点和相连的节点使用链表相连,便于区间查找和遍历。
推荐看张洋的 MySQL索引背后的数据结构及算法原理 这篇文章