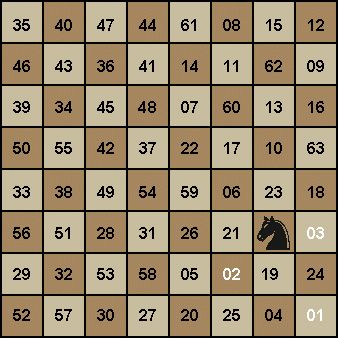
在一个国际象棋棋盘上,一个棋子“马” (骑士),按照“马走日”的规则,从一个格子出发,要走遍所有棋盘格恰好一次。把一个这样的走棋序列称为一次“周游
在8×8的国际象棋棋盘上,合格的“周游”数量有1.305×1035这么多,走棋过程中
失败的周游就更多了
采用图搜索算法,是解决骑士周游问题最容易理解和编程的方案之一
解决方案还是分为两步:
❖首先将合法走棋次序表示为一个图
❖采用图搜索算法搜寻一个长度为(行×列-1)的路径,路径上包含每个顶点恰一次
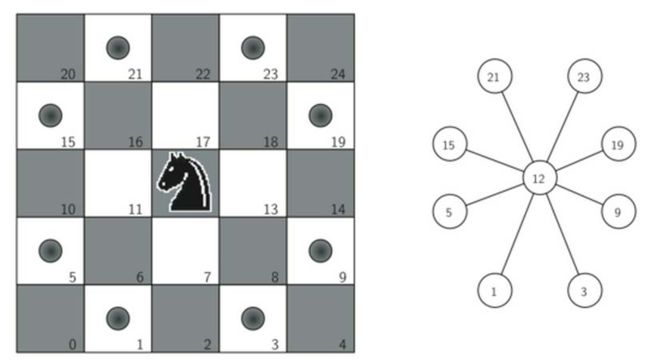
将棋盘和走棋步骤构建为图的思路
将棋盘格作为顶点,按照“马走日”规则的走棋步骤作为连接边,建立每一个棋盘格的所有合法走棋步骤能够到达的棋盘格关系图
合法走棋位置函数
def genLegalMoves(x, y , bdSize):
newMoves = []
moveOffsets =[(-1,-2),(-1,2),(-2,-1),(-2,1),
( 1,-2),( 1,2),( 2,-1),( 2,1)]
for i in moveOffsets:
newX = x + i[0]
newY = y + i[1]
if legalCoord(newX, bdSize) and legalCoord(newX, bdSize):
newMoves.append((newX, newY))
return newMoves
#是否超出棋盘范围
def legalCoord(x, bdSize):
if x >= 0 and x < bdSize:
return True
else:
return False
构建走棋关系图
def posToNodeID(row, col, bdSize):
return row*bdSize + col
def knightGraph(bdSize):
ktGraph = Graph()
for row in range(bdSize):
for col in range(bdSize):
nodeid = posToNodeID(row, col, bdSize)
newPositions = genLegalMoves(row, col, bdSize)
for e in newPositions:
nid = posToNodeID(e[0], e[1], bdSize)
ktGraph.addEdge(nodeid, nid)
return ktGraph
算法实现
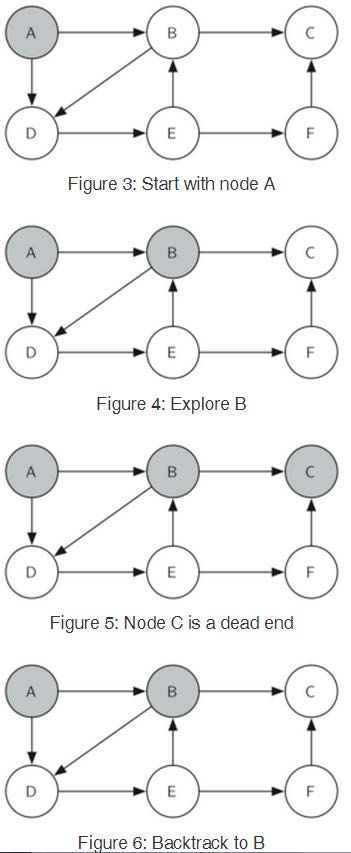
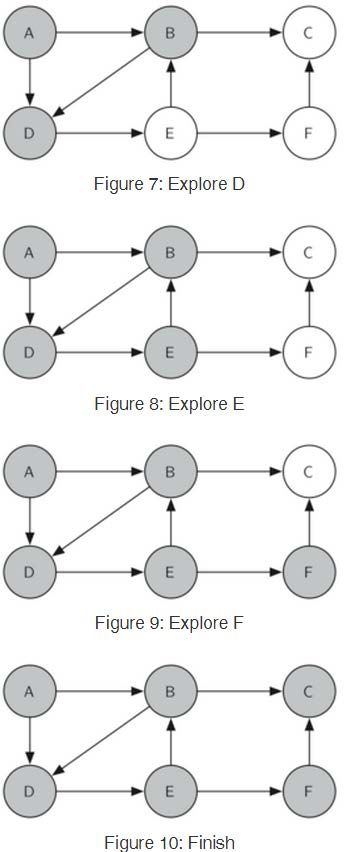
❖用于解决骑士周游问题的图搜索算法是深度优先搜索(Depth First Search)
❖相比前述的广度优先搜索,其逐层建立搜索树的特点
❖深度优先搜索是沿着树的单支尽量深入向下搜索
(如果到无法继续的程度还未找到问题解就回溯上一层再搜索下一支)
DFS的两个实现算法
一个DFS算法用于解决骑士周游问题,其特点是每个顶点仅访问一次
另一个DFS算法更为通用,允许顶点被重复访问,可作为其它图算法的基础
深度优先搜索解决骑士周游的关键思路:
如果沿着单支深入搜索到无法继续(所有合法移动都已经被走过了)时,路径长度还没有达到预定值(8×8棋盘为63)那么就清除颜色标记,返回到上一层换一个分支继续深入搜索
引入一个栈来记录路径,并实施返回上一层的回溯操作
def knightTour(n,path,u,limit):#n:层次,path:路径,u:当前顶点,limit:搜索总深度
u.setColor('gray')
path.append(u)#当前顶点加入路径
done = False
if n < limit:
nbrLst = list(u.getConnections())#对所有合法移动逐一深入
i = 0
while i < len(nbrLst) and not done:
if nbrLst[i].getColor() == 'white':
done = knightTour(n+1,path,nbrLst[i],limit)#nbrLst[i]递归深入
i+=1
if not done:
path.pop()
u.setColor('white')
else:
done = True
return done
上述算法的性能高度依赖于棋盘大小:
就5×5棋盘,约1.5秒可以得到一个周游路径,但8×8棋盘,则要半个小时以上才能得到一个解
目前实现的算法,其复杂度为O(kn),其中n是棋盘格数目,这是一个指数时间复杂度的算法!其搜索过程表现为一个层次为n的树
骑士周游算法改进
对nbrList的灵巧构造,以特定方式排列顶点访问次序
可以使得8×8棋盘的周游路径搜索时间降低到秒级!
这个改进算法被特别以发明者名字命名:Warnsdorff算法
初始算法中nbrList,直接以原始顺序来确定深度优先搜索的分支次序
新的算法,仅修改了遍历下一格的次序,将u的合法移动目标棋盘格排序为:具有最少合
法移动目标的格子优先搜索
def orderbyAvail(n):
resultLst = []
for v in n.getConnections():
if v.getColor() == 'white':
c = 0
for w in v.getConnections():
if w.getColor() == 'white':
c+=1
resultLst.append((c,v))
resultLst.sort(key=lambda x:x[0])
return [y[1] for y in resultLst]
完整代码:
Graph类
import sys
class Vertex:
def __init__(self,key):
self.id = key
self.connectedTo = {}
self.color = 'white'
self.dist = sys.maxsize
self.pred = None
def setColor(self, color):
self.color = color
def setDistance(self, d):
self.dist = d
def setPred(self, p):
self.pred = p
def getPred(self):
return self.pred
def getDistance(self):
return self.dist
def getColor(self):
return self.color
def addNeighbor(self,nbr,weight):
self.connectedTo[nbr] = weight
def __repr__(self):
return f'{self.id} connectto:' + str([v.id for v in self.connectedTo])
def getConnections(self):
return self.connectedTo.keys()
def getId(self):
return self.id
def getWeight(self,nbr):
return self.connectedTo[nbr]
class Graph:
def __init__(self):
self.verList = {}
self.num = 0
def addVertex(self, key):
self.num += 1
v = Vertex(key)
self.verList[key] = v
return v
def getVertex(self,key):
if key in self.verList:
return self.verList[key]
else:
return None
def __contains__(self, key):
return key in self.verList
def addEdge(self,fromkey,tokey,cost=0):
if fromkey not in self.verList:
self.addVertex(fromkey)
if tokey not in self.verList:
self.addVertex(tokey)
self.verList[fromkey].addNeighbor(self.verList[tokey],cost)
def getVertices(self):
return self.verList.keys()
def __iter__(self):
return iter(self.verList.values())
if __name__ == '__main__':
g = Graph()
for i in range(6):
g.addVertex(i)
print(g.addVertex(i))
from basicGraph import Graph
def posToNodeID(row, col, bdsize):
return row*bdsize + col
def legalCoord(newX, bdsize):
if newX >= 0 and newX < bdsize:
return True
else:
return False
def genLegalMoves(x, y, bdsize):
movesLst = []
moveOffsets = [(-2,-1),(-1,-2),(-2,1),(1,-2),(2,-1),(-1,2),(1,2),(2,1)]
for tup in moveOffsets:
newX = x + tup[0]
newY = y + tup[1]
if legalCoord(newX,bdsize) and legalCoord(newY,bdsize):
movesLst.append((newX,newY))
return movesLst
def knightGraph(bdsize):
g = Graph()
for row in range(bdsize):
for col in range(bdsize):
nodeId = posToNodeID(row,col,bdsize)
newPosLst = genLegalMoves(row,col,bdsize)
for pos in newPosLst:
targetNodeID = posToNodeID(pos[0],pos[1],bdsize)
g.addEdge(nodeId,targetNodeID)
return g
def orderbyAvail(n):
resultLst = []
for v in n.getConnections():
if v.getColor() == 'white':
c = 0
for w in v.getConnections():
if w.getColor() == 'white':
c+=1
resultLst.append((c,v))
resultLst.sort(key=lambda x:x[0])
return [y[1] for y in resultLst]
def knightTour(n,path,u,limit):
u.setColor('gray')
path.append(u)
done = False
if n < limit:
# nbrLst = list(u.getConnections())
nbrLst = list(orderbyAvail(u))
i = 0
while i < len(nbrLst) and not done:
if nbrLst[i].getColor() == 'white':
done = knightTour(n+1,path,nbrLst[i],limit)
i+=1
if not done:
path.pop()
u.setColor('white')
else:
done = True
return done
if __name__ == '__main__':
g = knightGraph(8)
# for i in g:
# print(i)
path = []
startVertex = g.getVertex(4)
knightTour(0,path,startVertex,63)
for node in path:
print(node.getId(),end=' ')