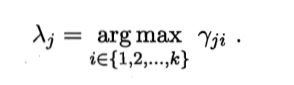文章脉络
1.什么是聚类
2.聚类的效果评估——性能度量
2.1外部指标
2.2内部指标3.聚类的类型
3.1原型聚类
3.2密度聚类
3.3层次聚类4.总结
1. 什么是聚类
“聚类”(clustering)算法是“无监督学习”算法中研究最多、应用最广的算法,它试图将数据集中的样本划分为若干个通常是不相交的子集,每个子集称为一个“簇”(cluster),每个簇可能对应于一些潜在的概念(也就是类别),如“浅色瓜” “深色瓜”,“有籽瓜” “无籽瓜”,甚至“本地瓜” “外地瓜”等;需说明的是,这些概念对聚类算法而言事先是未知的,聚类过程仅能自动形成簇结构,簇对应的概念语义由使用者来把握和命名。
通俗来说,聚类可以将一个数据集中所有样本根据相似度的大小分成若干组,使用者可以根据自己的目的来给每一组数据下定义。聚类的应用有很多,比如金融机构可以将客户群体分为高风险客户、中风险客户、低风险客户等,用聚类对某一区域企业进行评级管理等。
2. 聚类的效果评估——性能度量
通过聚类所得到的结果是好是坏,需要通过性能度量来评估。聚类性能度量又称聚类“有效性指标”,它是聚类过程中优化的目标,可以分为外部指标和内部指标,其中心思想都是使得簇内相似度尽可能高,簇间相似度尽可能低。
2.1 外部指标
外部指标:指将聚类结果与某个“参考模型”进行比较。
常用指标:
变量解释:
对于数据集D = {x1,x2,……xm},假定通过聚类给出的簇划分为C = {C1,C2,……Ck},参考模型给出的划分为C* = {C1*,C2*……Cs*},将样本两两配对,定义出四个集合:
a:在C中同簇,C*中也同簇
b:在C中同簇,C*中不同簇
c:在C中不同簇,C*中同簇
d:在C中不同簇,C*也不同簇
2.2 内部指标
内部指标:直接参考聚类的结果而不利用任何的参考模型。
常用指标:
变量解释:
avg(C):簇C内样本间的平均距离
diam(C):簇C内样本间的最远距离
dmin(Ci, Cj):两个簇最近的样本间的距离
dcen(Ci,Cj):两个簇中心点间的距离
1)距离计算
对于函数dist(·,·),若它是一个“距离度量”,则需满足四个性质
1.非负性:距离不为负
2.同一性:只有两点重合时距离才为0
3.对称性:A到B的距离等于B到A的距离
4.直递性:A到B再到C的距离之和要大于或等于从A直接到C的距离
有序属性的距离计算:
无序属性的距离计算:VDM
混合属性的距离计算:闵可夫斯基距离与VDM结合
【注意】:用于度量相似度的距离未必一定要满足“距离度量”的所有基本性质,尤其是直递性,这样的距离称为“非度量距离”。在不少现实任务中,有必要基于数据样本来确定合适的距离计算式,可以通过“距离度量学习”来实现。
3. 聚类的类型
3.1 原型聚类
1)k均值(k-means)算法
给定样本集D = {x1,x2,……xm},k均值算法针对聚类所得的簇划分C = {C1,C2,……Ck}最小化平方误差
直观上看,该式刻画了簇内样本围绕簇均值向量的紧密程度,E值越小则簇内样本相似度越高。最小化上式并不容易,需要考察样本集D所有可能的簇划分,这是一个NP难问题,因此k均值算法采用了贪心策略,通过迭代优化来近似求解上面的公式,算法流程如下:
优点:简单易实现,收敛快(一般5~10次)
缺点:
1.簇数k选择不同对结果影响很大
2.初始点的选择会影响聚类的结果,很可能使聚类只能收敛到局部最优,所以需要尝试不同的初始点
3.聚类过程中用到了均值,因此噪点对算法影响较大
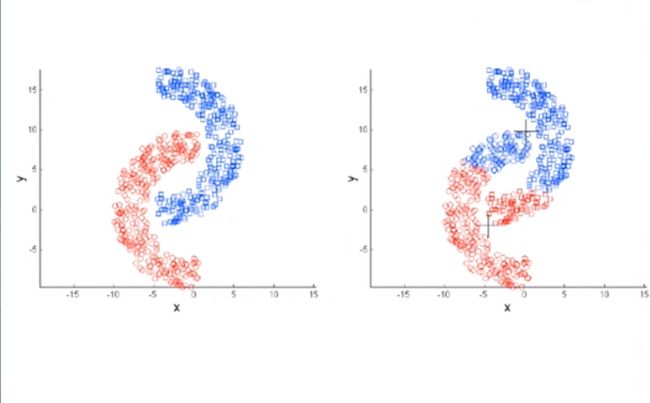
4.由于公式刻画的是样本围绕均值的紧密程度,因此k-means算法只适用于程球状分布的簇,如下图(我们想要的聚类效果是左图,但通过k-means算法聚类的效果是右图)
2)学习向量量化(LVQ)
LVQ假设数据样本带有类别标记Y = {y1,y2,……ym},学习过程利用样本的这些监督信息来辅助聚类,其流程是
第1行,初始化 p 个原型向量(数据集中有几个类别,p就为几),随机从每个类别中选择一个数据样本作为该类别的初始原型向量。第6-9行表示如果 pi*的类别标记与 xj 的类别标记相同,则原型向量 pi* 向 xj 方向靠拢;如果 pi*的类别标记与 xj 的类别标记不同,则原型向量 pi* 向 xj 方向远离,该过程迭代到满足条件停止。
LVQ算法优点:1.收敛较快; 2.相对于k-means算法对噪点较不敏感
LVQ算法缺点:1.原型向量的初始值和学习率对聚类的结果影响较大
3)高斯混合聚类
高斯混合聚类采用概率模型来表达聚类原型
其中p(x丨ui,Σi)表示样本集中每个混合成分(高斯分布)的概率密度函数,ui为均值向量,Σi为协方差矩阵,αi为各成分的混合系数(概率)。
假设样本的生成过程由高斯混合分布给出,然后根据被选择的混合成分的概率密度函数进行采样得到相应样本。令zj ∈{1,2,……k},表示生成xj的高斯混合成分,其取值未知,p(zj = i)=αi,根据贝叶斯定理,zj的后验分布对应于
记 γji(i=1,2,……k)= pm(zj = i 丨xj)
从原型聚类的角度来看,高斯混合分布采用高斯分布概率模型对原型进行刻画,簇划分则由原型对应后验概率确定,簇标记λi
在高斯混合聚类中,我们需要学习的参数是,αi,ui,Σi,其流程为:
第2-12行是基于EM算法对模型的参数进行迭代更新,具体内容可参考贝叶斯分类章节,或者参考B站视频便于理解:高斯混合聚类
第12行的停止条件可以是:达到最大迭代数,公式(9.29)的似然函数LL(D)趋于不再增长
高斯混合聚类优点:1.收敛速度快; 2.能扩展以用于大规模的数据集
高斯混合聚类缺点:1.中心选择和噪点对聚类结果影响大
3.2 密度聚类
对于样本分布不规则的聚类,密度聚类是一种很好的方法,如下图的分布
在密度聚类中,DBSCAN是一种著名的密度聚类算法,它基于一组“邻域”参数(e,MinPts)来刻画样本分布的紧密程度。算法涉及到的概念:
“e - 邻域”:在xj样本以e为半径范围内的所有样本的集合
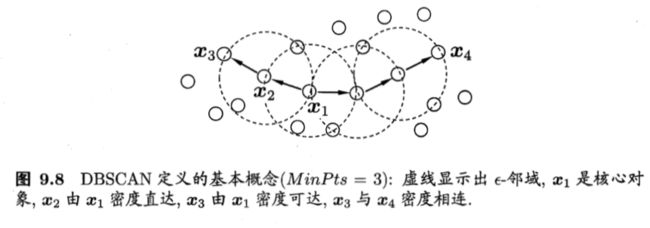
核心对象:当样本 xj的 “e - 邻域”内含有至少 MinPts 个样本时,该样本 xj 是一个核心对象
密度直达:若 xj 位于 xi 的 “e - 邻域”中,且 xi 是核心对象,则称 xj 与 xi 密度直达
密度可达:若 xi 与 xj 能通过一系列密度直达的点关联起来,则 xi 与 xj 密度可达
密度相连:若 xi 与 xj 都能通过 xk 密度可达,则称 xi 与 xj 密度相连
基于以上概念,NBSCAN算法的目的是:从数据集D中,找出满足某些性质的聚类簇。这些性质是
NBSCAN算法的流程是:
第10-24行表示随机从核心对象集合中抽取出一个核心对象,根据这个核心对象找出其密度相连的所有样本集合,将这些样本集合设定为一个簇,将该簇集合中出现的核心对象从核心对象集合中移除,依次不断迭代,最后获得聚类计算的结果簇划分。
【注意】通过DBSCAN算法完成聚类后,会有一些样本不属于任何一个簇,它们被认为是噪点,或者是异常样本。在个别应用场景下,这部分样本将具有较高的价值,比如在反欺诈场景下,这部分不合群的样本数据是欺诈行为数据的概率较高。
DBSCAN算法优点:1.不需事先确定簇数k;2.适用于任意形状分布的样本数据; 3.能够识别出噪点;
DBSCAN算法缺点:1.当数据维度较高,样本分布比较松散时,密度可能很难定义;2.参数e和MinPts的取值对结果影响很大
3.3 层次聚类
层次聚类试图在不同层次对数据集进行划分,从而形成树形的聚类结构。数据集的划分可采用“自底向上”的聚合策略,也可采用“自顶向下”的分拆策略。AGNES是一种采用自底向上聚合策略的聚类算法,它先将每个样本都作为一个簇,然后在算法运行的每一步找出距离最近的两个聚类簇进行合并,该过程不断重复,直到达到预设的聚类簇个数。流程如下:
输入中,距离度量函数可以选择dmin,dmax,davg来进行,相应的AGNES被称为“单链接”算法,“全链接”算法,“均链接”算法。
以西瓜数据集4.0为例,令AGNES算法一直执行到所有样本出现在同一个簇中(即k=1),得到的树状图如下,我们可以根据簇数的要求进行“切割”,比如我们需要分出7个簇,只需令k=7即可。
AGNES算法优点:1.距离和相似度的规则容易定义,限制少; 2.可以发现簇的层次关系; 3.可以聚类成其它形状
AGNES算法缺点:1.计算复杂度高; 2.奇异值能产生很大影响; 3.算法很可能聚类成链状
4. 总结
1)基于不同的学习策略,聚类可分为原型聚类、密度聚类、层次聚类等
2)聚类的性能度量思想是:簇内相似度高,且簇间相似度低
3)相似度的衡量依赖于距离的计算
4)聚类生成的簇需要使用者来把握和命名
5)不同条件适用不同的聚类方法:
a.样本程球状分布时:k-means算法
b.样本分布不规则时:密度聚类、层次聚类
c.需要事先决定簇数时:原型聚类、层次聚类
d.需要发现噪点时:密度聚类
e.样本带有标记时:LVQ算法
f.样本量很大时:高斯混合聚类
……