最近两年一直在做数据处理和模型的建立及优化,贝叶斯作为最为基本的算法之一,是需要技术团队掌握的。以下结合笔者的经验将贝叶斯的使用做个粗略的总结。记住一点,在处理很多不确定因素的推理过程,贝叶斯由于自身DAG的结构,在机器学习中有着自然的优势。
当然,假设你知道训练集和测试集的关系。简单来讲是我们要在训练集上学习一个模型,然后拿到测试集去用,效果好不好要根据测试集的错误率来衡量。但很多时候,我们只能假设测试集和训练集的是符合同一个数据分布的,但却拿不到真正的测试数据。也验证了朴素贝叶斯这种高偏差低方差的算法。好在实现起来简单,运算复杂度相对较低,我们在有充足的样本数据的条件下做一些简单的借款预测是可以的,但由于贝叶斯对输入数据的敏感程度,不建议直接用在一款新的产品上,哪怕只是件均、还款方式或期限、借款利率有差异。在我们的真实项目进程中,贝叶斯更多帮我们做了特征工程中的特征选择和特征剔除及基本的训练,更多的验证工作在别的算法模型中进行实践。在模型冷启动的过程中,贝叶斯也被我们用作生产验证模型的一种。
贝叶斯决策论的使用
当然整个贝叶斯的算法使用要建立在一定的数学条件下,贝叶斯决策就是在某个先验分布下使得平均风险最小的决策。与之匹配的作为参数估计使用的两种重要方法(极大似然估计和极大后验概率估计)先验概率与后验概率的基本定义参见百度。但是大体的理解就是先验概率是我们老百姓说法的概率,后验概率是所谓的条件概率。(频率统计学派和贝叶斯统计学派。目前,国内的数理统计主要是频率统计)
在我们的信贷风控体系模型搭建过程中,实际上纯正的贝叶斯决策用的没有想象中的多。我们可以看看针对朴素贝叶斯的例子
朴素贝叶斯
朴素贝叶斯算法做了一假设:“朴素的认为各个特征相互独立”
1、离散型朴素贝叶斯:所有维度的特征都是离散型的随机变量(核心算法就是记数)
2、连续性朴素贝叶斯:所有维度的特征都是连续性随机变量
3、混合型朴素贝叶斯:各个维度的特征有离散型的,也有朴素型的
先来个最简单的例子,只看贷款期限和借款人年龄与借款逾期状况的匹配程度:
Index(['age', 'day', 'status'], dtype='object')
#设置特征X
X=np.array(loan_status[['age','day']])
#设置目标Y
Y=np.array(loan_status['status'])
....
#利用Python自带的连续性朴素贝叶斯模型
clf=GaussianNB()
clf.fit(X_train,y_train)`
GaussianNB(priors``=``None``)`
#使用测试集数据对训练后的模型进行测试,模型预测的准确率为69%。
#使用测试集数据检验模型准确率
clf.score(X_test,y_test)
# 准确率结果值`0.68787878787878787`
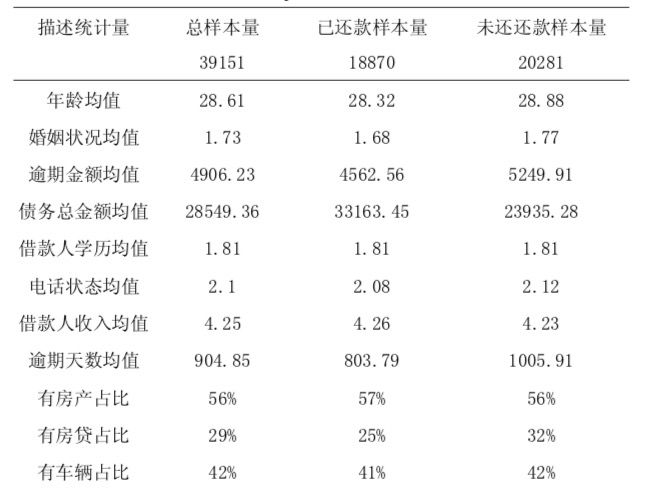
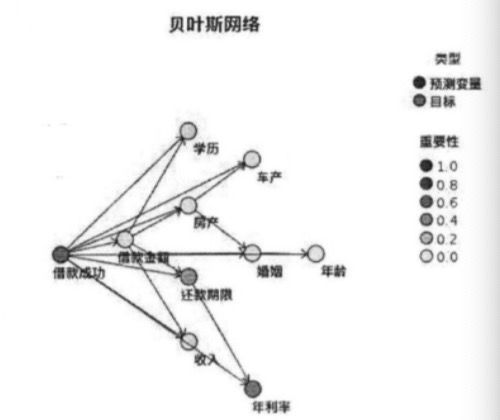
上面的例子可以用来判断一个二维的属性的借款人的逾期预测效果,当然在实际工作过程中这么简单的训练及模型建立过程几乎是不存在的。给一个稍微复杂点的例子,比如说针对以下维度:
NaiveBayes(formula=当前状态~性别+年龄+婚姻状况+逾期金额+债务总额+学 历+借款人收入+房产+房贷+逾期天数 +电话接听状态,data=train_data)
这里面增加了很多参数,
当然,后面我们还会聊聊LR模型的时候会提到如何去剔除未通过显著性校验的数据。Spark对贝叶斯的支持一样很简单,
importorg.apache.spark.mllib.classification.NaiveBayes
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.{SparkContext,SparkConf}
object naiveBayes {
def main(args: Array[String]) {
val conf =new SparkConf()
val sc =new SparkContext(conf)
//读入数据
val data = sc.textFile(args(0))
val parsedData =data.map { line =>
val parts =line.split(',')
LabeledPoint(parts(0).toDouble,Vectors.dense(parts(1).split(' ').map(_.toDouble)))
}
// 把数据的60%作为训练集,40%作为测试集.
val splits = parsedData.randomSplit(Array(0.6,0.4),seed = 11L)
val training =splits(0)
val test =splits(1)
//获得训练模型,第一个参数为数据,第二个参数为平滑参数,默认为1,可改
val model =NaiveBayes.train(training,lambda = 1.0)
//对模型进行准确度分析
val predictionAndLabel= test.map(p => (model.predict(p.features),p.label))
val accuracy =1.0 *predictionAndLabel.filter(x => x._1 == x._2).count() / test.count()
println("accuracy-->"+accuracy)
println("Predictionof (0.0, 2.0, 0.0, 1.0):"+model.predict(Vectors.dense(0.0,2.0,0.0,1.0)))
}
}
另外,CSDN有篇文章适合大家参考(https://blog.csdn.net/weixin_40671804/article/details/84305384)
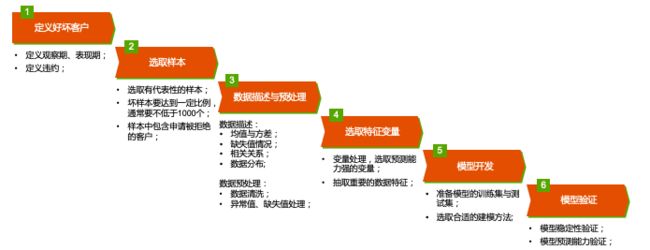
其实说到这里,关于朴素贝叶斯的常规性用法就这些,流程不变还是数据清洗,数据验证,特征工程,然后建模跑数据,再做模型的优化(无非找到损失函数最小的方式)看IV,WOE来进行比较调整。做评估前也要做好特征的归一化。
std = StandardScaler()
X_train = std.fit_transform(X_train.values)
X_test = std.transform(X_test.values)
看变量名就知道这两个数据集是干啥的吧。
这个流程是我司一直在使用的整体流程,在任何项目上,不会因为模型的选择发生变化。祝大家学习快乐,下一章我们聊聊决策树。