Sklearn（v3）——SVM理论(3)

C越小，力度越大，一般从0开始逐渐调大

#调线性核函数
score = []
C_range = np.linspace(0.01,30,50)
for i in C_range:
    clf = SVC(kernel="linear",C=i,cache_size=5000).fit(Xtrain,Ytrain)
    score.append(clf.score(Xtest,Ytest))
print(max(score), C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()

结果：

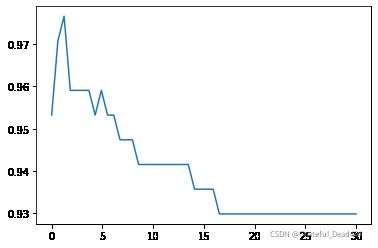
0.9766081871345029 1.2340816326530613

 

#换rbf
score = []
C_range = np.linspace(0.01,30,50)
for i in C_range:
    clf = SVC(kernel="rbf",C=i,gamma = 
0.012742749857031322,cache_size=5000).fit(Xtrain,Ytrain)
    score.append(clf.score(Xtest,Ytest))
print(max(score), C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()

结果： 

0.9824561403508771 6.130408163265306

 

#进一步细化
score = []
C_range = np.linspace(5,7,50)
for i in C_range:
    clf = SVC(kernel="rbf",C=i,gamma = 
0.012742749857031322,cache_size=5000).fit(Xtrain,Ytrain)
    score.append(clf.score(Xtest,Ytest))
print(max(score), C_range[score.index(max(score))])
plt.plot(C_range,score)
plt.show()

结果：  

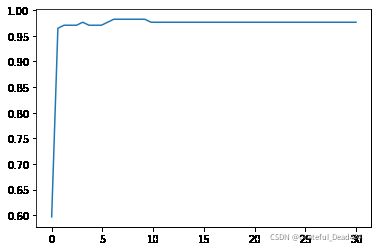
0.9824561403508771 5.938775510204081

  

复习

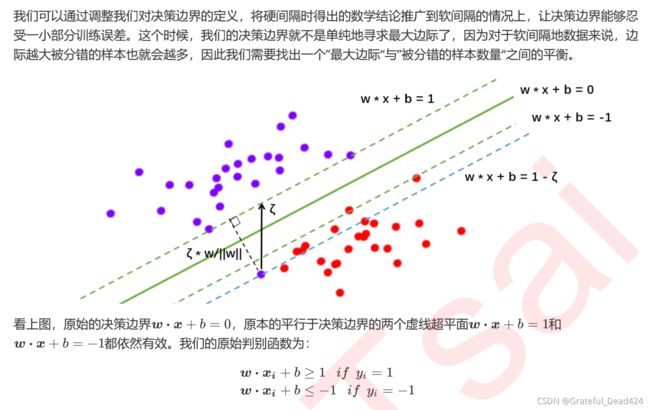
决策边界——>虚拟超平面——> 核函数

松弛系数（硬间隔——>软间隔）

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import svm
from sklearn.datasets import make_circles , make_moons, make_blobs,make_classification

n_samples = 100

datasets = [
make_moons(n_samples=n_samples, noise=0.2, random_state=0),
make_circles(n_samples=n_samples, noise=0.2, factor=0.5, random_state=1),
make_blobs(n_samples=n_samples, centers=2, random_state=5),
make_classification(n_samples=n_samples,n_features =
2,n_informative=2,n_redundant=0, random_state=5)
]

Kernel = ["linear"]

#四个数据集分别是什么样子呢？
for X,Y in datasets:
    plt.figure(figsize=(5,4))
    plt.scatter(X[:,0],X[:,1],c=Y,s=50,cmap="rainbow")

nrows=len(datasets)
ncols=len(Kernel) + 1

fig, axes = plt.subplots(nrows, ncols,figsize=(10,16))

#第一层循环：在不同的数据集中循环
for ds_cnt, (X,Y) in enumerate(datasets):
    ax = axes[ds_cnt, 0]
    if ds_cnt == 0:
        ax.set_title("Input data")
    ax.scatter(X[:, 0], X[:, 1], c=Y, zorder=10, cmap=plt.cm.Paired,edgecolors='k') 
    ax.set_xticks(())
    ax.set_yticks(())

    for est_idx, kernel in enumerate(Kernel):
        ax = axes[ds_cnt, est_idx + 1]
        clf = svm.SVC(kernel=kernel, gamma=2).fit(X, Y)
        score = clf.score(X, Y)
        ax.scatter(X[:, 0], X[:, 1], c=Y,zorder=10,cmap=plt.cm.Paired,edgecolors='k')
        ax.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,facecolors='none', zorder=10, edgecolors='white')

        x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
        y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5

        XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
        Z = clf.decision_function(np.c_[XX.ravel(), YY.ravel()]).reshape(XX.shape) 
        ax.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.Paired)
        ax.contour(XX, YY, Z, colors=['k', 'k', 'k'], linestyles=['--', '-', '--'], levels=[-1, 0, 1])
        
        ax.set_xticks(())
        ax.set_yticks(())

        if ds_cnt == 0:
            ax.set_title(kernel)

        ax.text(0.95, 0.06, ('%.2f' % score).lstrip('0')
            , size=15
            , bbox=dict(boxstyle='round', alpha=0.8, facecolor='white')
            #为分数添加一个白色的格子作为底色
            , transform=ax.transAxes #确定文字所对应的坐标轴，就是ax子图的坐标轴本身
            , horizontalalignment='right' #位于坐标轴的什么方向
            )

plt.tight_layout()
plt.show()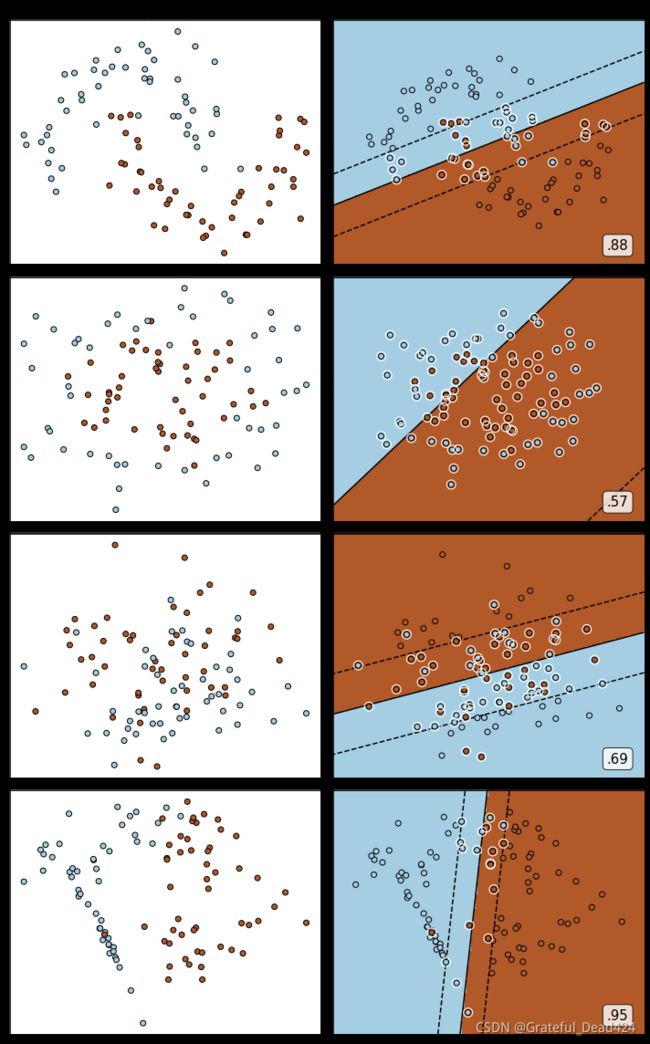

白色圈圈出的就是我们的支持向量，大家可以看到，所有在两条虚线超平面之间的点，和虚线超平面外，但属于另 一个类别的点，都被我们认为是支持向量。并不是因为这些点都在我们的超平面上，而是因为我们的超平面由所有的这些点来决定，我们可以通过调节C来移动我们的超平面，让超平面过任何一个白色圈圈出的点。参数C就是这样影响了我们的决策，可以说是彻底改变了支持向量机的决策过程。