【机器学习sklearn】支持向量机SVM

---

一、SVM是什么？

支持向量机（Support Vector Machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

二、算法原理

SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。

1.超平面

在样本空间中，划分超平面线性方程为：$w^{T}x+b=0$。
其中，$w=(w_1,w_2,...,w_d)$为法向量，决定超平面方向；$b$为位移项，决定超平面与原点之间的距离。记为$(w,b)$。

样本空间中任意点$x$到超平面$(w,b)$的距离为：
$$r=\frac{w^T{x}_i+b}{||w||}$$

• 超平面方程不唯一
• 法向量$w$和位移项$b$确定一个唯一的超平面
• 法向量$w$垂直于超平面
• 法向量$w$指向的空间一半为正空间，一半为负空间

2.几何间隔

给定数据集$X$和超平面$w^{T}x+b=0$，定义数据集$X$中的任意一个样本点$(x_i,y_i)，y_i\in -1，1，i=1,2,...,m$，关于超平面的几何间隔为：
$$r_i=\frac{y_i(w^{T}x+b)}{||w||}$$
数据集$X$中所有样本点的几何间隔最小值：
$$r_i=\underset{i=1,2,...,m}{\min }{r}_i$$

3.支持向量机

假设超平面$(w,b)$将训练样本正确分类：

$$\{\begin{array}{ll}{w}^T{x}_i+b\ge +1,& \text{yi=+1}\\ w^T{x}_i+b\le -1,& \text{yi=−1}\end{array}$$

距离超平面最近的几个训练样本点使得$w^T{x}_i+b=1$，$w^T{x}_i+b=-1$，则称为“支持向量”（support vector）。

间隔（margin），即两个异类支持向量到超平面距离之和：
$$r=\frac{2}{||w||}$$

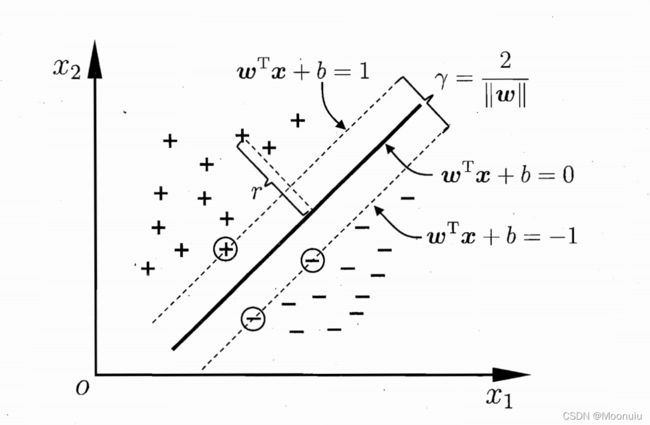
支持向量机就是找距离正负样本都最远的超平面。
将找“最大间隔”（maximum margin）的划分超平面转化为带约束条件的优化问题，找到约束参数$w$和$b$，使得$r$最大，即为：
$$\underset{w,b}{\max }\frac{2}{||w||}s.t.y_i(w^T{x}_i+b)\ge 1，i=1,2,...,m$$
等价于
$$\underset{w,b}{\min }\frac{1}{2}||w|{|}^{2}s.t.y_i(w^T{x}_i+b)\ge 1，i=1,2,...,m$$
以上为支持向量机SVM的基本型。

4.对偶问题

上面提到的支持向量机SVM的基本型公式，本身是一个凸二次规划（convex quadratic programming）问题。对其使用拉格朗日乘子法可得到“对偶问题”（dual problem），该问题的拉格朗日函数为：
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\alpha }_i(1-y_i(w^T{x}_i+b))$$
其中$\alpha =({\alpha }_1,{\alpha }_2,...,{\alpha }_m)$
对偶问题：
$$\underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$
$$\begin{gathered} s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0 \\ {\alpha }_i\ge 0，i=1,2,...,m \end{gathered}$$
KKT（Karush-Kuhn-Tucker）条件:
$$\{\begin{array}{l}{\alpha }_i\ge 0;\\ y_{i}f(x_i)-1\ge 0;\\ {\alpha }_i(y_{i}f(x_i)-1)=0;\end{array}$$

三、软间隔与支持向量回归

1. 软间隔

在现实任务中，原始样本空间内也许并不存在一个能正确划分两类样本的超平面，即线性不可分问题。
缓解该问题的一个方法是引入“软间隔”（soft margin）的概念，允许支持向量机犯错，即允许某些样本不满足约束条件。而“硬间隔”（hard margin）则是要求所有样本均满足约束，即所有样本都必须划分正确。

上图为软间隔示意图，红色圈圈为不满足约束 $y_i(w^T{x}_i+b)\ge 1$的样本。
优化目标：
$$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{l}_{0/1}(y_i(w^T{x}_i+b)-1)$$
其中，$C>0$是一个常数，$l_{0/1}$是“0/1损失函数”。
三种常见的替代损失（surrogate loss）函数：hinge损失、指数损失、对率损失。

2. 支持向量回归（Support Vector Regression，SVR）

假设能容忍$f(x)$与$y$之间最多有$ϵ$的偏差，即仅当$f(x)$与$y$之间的差别绝对值大于$ϵ$时才计算损失。

红色显示出$ϵ$-间隔带，落入其中的样本不计算损失。

四、核函数（kernel function）

对于线性不可分问题，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。

如上图，将原始的二维空间映射到一个合适的三维空间，就能找到一个合适的划分超空间。
令$\varphi (x)$表示将$x$映射后的特征向量，在特征空间中划分超平面所对应的模型可表示为：
$$f(x)=w^T\varphi (x)+b$$
其中，$w$和$b$是模型参数。
由于特征空间维数可能很高，甚至可能是无穷维，直接计算$\varphi (x_i{)}^T\varphi (x_j)$有难度。所以设计了一个函数：
$$\kappa (x_i,x_j)=<\varphi (x_i),\varphi (x_j)>=\varphi (x_i{)}^T\varphi (x_j)$$
“核技巧”kernel trick，即$x_i$和$x_j$在特征空间的内积等于它们在原始样本空间中通过核函数$\kappa (\cdot ,\cdot )$ 计算的结果。
模型最优解核函数展开式，“支持向量展式”：
$$\begin{gathered} f(x)=w^T\varphi (x)+b \\ =\sum _{i=1}^m{\alpha }_i{y}_i\varphi (x_i{)}^T\varphi (x)+b \\ =\sum _{i=1}^m{\alpha }_i{y}_i\kappa (x,x_i)+b \end{gathered}$$

几种常用的核函数：

其中，$d=1$时退化为线性核。高斯核亦称为RBF核（Radial Basis Function，径向基函数）。

实例

class sklearn.svm.SVC(*, C=1.0, kernel='rbf', degree=3, gamma='scale', coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=- 1, decision_function_shape='ovr', break_ties=False, random_state=None)

• C：惩罚系数，防止模型过拟合；
• kernel：核函数，包括{‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’}；
• degree：多项式核函数的维度；
• gamma：核函数系数，只作用于 rbf、poly、sigmoid 三个核函数；
• coef0：常数项，只作用于poly 和 sigmoid 核函数；
• shrinking：启用启发式收缩；当迭代次数过大时， 启用启发式收缩可以缩短训练时间；
• probability：启用概率估计；
• tol：停止拟合容忍度；
• cache_size：核缓存大小；
• class_weight：类别的权重；
• verbose：启用详细输出日志；
• max_iter：最大迭代次数，-1表示不限制迭代次数；
• decision_function_shape：多分类策略；
• break_ties：启用打破平局，多分类任务时启用；
• random_state：随机数。

1. 线性SVM

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm

data = np.array([
    [0.1, 0.7],
    [0.3, 0.6],
    [0.4, 0.1],
    [0.5, 0.4],
    [0.8, 0.04],
    [0.42, 0.6],
    [0.9, 0.4],
    [0.6, 0.5],
    [0.7, 0.2],
    [0.7, 0.67],
    [0.27, 0.8],
    [0.5, 0.72]
])
label = [1] * 6 + [0] * 6
# 获取数据值所在的范围
x_min, x_max = data[:, 0].min() - 0.2, data[:, 0].max() + 0.2
y_min, y_max = data[:, 1].min() - 0.2, data[:, 1].max() + 0.2
# 生成网格坐标矩阵
# numpy.meshgrid从坐标向量中生成网格坐标矩阵。对于评估网格上的函数非常有用。
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.002),
                     np.arange(y_min, y_max, 0.002)) # meshgrid如何生成网格
# 支持向量机（svm）线性模型,SVC为Support Vector Classification支持向量分类器
# kernel='linear' 线性核函数；C：正则化系数，float类型，默认值为1.0，用来防止模型过拟合。C越小，泛化能力越强
model_linear = svm.SVC(kernel='linear', C = 0.001)
model_linear.fit(data, label)  # 训练模型
Z = model_linear.predict(np.c_[xx.ravel(), yy.ravel()])  # 预测
# 变形
Z = Z.reshape(xx.shape)
# 绘制三维等高线图（contourf会填充轮廓）
plt.contourf(xx, yy, Z, cmap = plt.cm.ocean, alpha=0.6)
# 散点图
plt.scatter(data[:6, 0], data[:6, 1], marker='o', color='r', s=100, lw=3)
plt.scatter(data[6:, 0], data[6:, 1], marker='x', color='k', s=100, lw=3)
plt.title('Linear SVM')
plt.show()

2. 多项式SVM

for i, degree in enumerate([1, 3, 5, 7, 9, 12]):
    # C: 惩罚系数，kernel='poly'：多项式核函数
    model_poly = svm.SVC(C=0.0001, kernel='poly', degree=degree)  # 多项式核
    model_poly.fit(data, label)
    # ravel - flatten
    # c_ - vstack
    # 把后面两个压扁之后变成了x1和x2，然后进行判断，得到结果在压缩成一个矩形
    Z = model_poly.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # 绘制多个子图,subpot() 方法在绘图时需要指定位置，subplots() 方法可以一次生成多个，在调用时只需要调用生成对象的 ax 即可
    plt.subplot(3, 2, i + 1)
    plt.subplots_adjust(wspace=0.4, hspace=0.4)
    plt.contourf(xx, yy, Z, cmap=plt.cm.ocean, alpha=0.6)  # 等高线图

    # 画出训练点
    plt.scatter(data[:6, 0], data[:6, 1], marker='o', color='r', s=100, lw=3)
    plt.scatter(data[6:, 0], data[6:, 1], marker='x', color='k', s=100, lw=3)
    plt.title('Poly SVM with $\degree=$' + str(degree))

4. 高斯核SVM

for i, gamma in enumerate([1, 5, 15, 35, 45, 55]):
    # C: 惩罚系数，kernel='rbf'：高斯核函数，gamma: 高斯核的系数
    model_rbf = svm.SVC(kernel='rbf', gamma=gamma, C=0.0001).fit(data, label)

    Z = model_rbf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    plt.subplot(3, 2, i + 1)
    plt.subplots_adjust(wspace=0.4, hspace=0.4)
    plt.contourf(xx, yy, Z, cmap=plt.cm.ocean, alpha=0.6)

    # 画出训练点
    plt.scatter(data[:6, 0], data[:6, 1], marker='o', color='r', s=100, lw=3)
    plt.scatter(data[6:, 0], data[6:, 1], marker='x', color='k', s=100, lw=3)
    plt.title('RBF SVM with $\gamma=$' + str(gamma))

---

参考链接：
[1]: https://zhuanlan.zhihu.com/p/31886934
[2]: 机器学习（西瓜书）, 周志华
[3]: https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html
[4]: https://blog.csdn.net/weixin_42279212/article/details/121504641