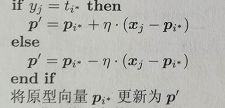聚类分析常见方法:
原型聚类(主要K-Means聚类);层次聚类;密度聚类
1.原型聚类(K-Means聚类、学习向量量化LVQ、高斯混合聚类GMM)
2.层次聚类(AGNES)
3.密度聚类(DBSCAN)
K-Means聚类
1. 先随机选取k个聚类中心(又称均值向量);
2. 计算各样本到各聚类中心的距离,根据k个距离,将各个样本分簇;
3. 从k个簇中求出新的聚类中心;
4. 按2、3更新聚类中心,不断重复以上过程,直至迭代差异小于设定值。
但K-Means聚类,首次随机选取的聚类中心会影响最终的聚类分簇结果。
学习向量量化 LVQ
LVQ的样本带有类别标记,利用这些标记辅助聚类,属于监督学习范畴
(说在前面:每个原型向量代表一个聚类簇。但是,原型向量的个数 与 类别标记的种类不一定要相等,多个原型向量可以时同一个类型标记。)
1. 初始化一组原型向量;
2. 从样本中随机选取样本,计算样本到原型向量的距离,找出距离最近的原型向量p*
3.
4. 重复2、3直至满足迭代终止条件,输出最终原型向量。
其中:第3步表示,当该样本对应的p*与其类型标记相同,则该原型向量向样本方向靠拢;当其p*与其标记不同,则向样本方向远离。
高斯混合聚类 GMM
假定所有样本是由k个混合多元高斯分布组组成的混合分布生成的。
1. 初始化k个多元高斯分布及其权重;
2. 根据概率统计中的贝叶斯定理,得到每个样本在k个分布下的后验分布(与条件概率类似);
3. 根据均值、协方差、后验概率,更新均值向量、协方差矩阵、权重;
4. 重复2、3,直至迭代满足终止条件;
5. 对每个样本点,计算相对k个簇的后验概率,归于最大后验概率的簇。
层次聚类 Hierarchical methods
1. 计算各样本与样本之间的距离,按合并规则合并为一类;
2. 计算各类与类之间的距离,按合并规则合并成一个大类;
3. 不断合并,直至最终合成一个类
其中,类与类之间合并的规则有:最短距离法、最长距离法、中间距离法、类平均法等。
实现算法有:
BIRCH(Balanced Iterative Reducing and Clustering Using Hierarchies)、ROCK、Chameleon、KNN(k-nearest-neighbor)
优点:
1. 距离和规则的相似度容易定义,限制少;
2. 不需预先指定聚类数;
3. 体现类之间的层次关系;
4. 可聚类成其它形状
缺点:
计算复杂度太高;受奇异值影响大;可能聚类成链
密度聚类 DBSCAN
需要 ε-邻域 和形成高密度区域所需的最少点数。
1. 随机选取未被访问过的点,检验其ε-邻域内是否有足够点数。
2. 若有,则以该邻域内点建立一类;若没有,则这个点被标记为噪音。
3. 循环1,若原标记被噪音的点之后含于某符合要求的ε-邻域,则也可聚为其类。
算法有:OPTICS算法(Ordering points to identify the clustering structure)
优点:对噪音不敏感,可以聚成任意形状
缺点:对参数的依赖性强
谱聚类
是一种基于图论的聚类方法
聚类原则为:将带权无向图(相似度矩阵)划分为两个或两个以上的最优子图,使子图内部尽量相似,而子图间距离尽量距离较远。
聚类性能度量指标:
外部指标:Jaccard系数(JC)、FM指数(FMI)、Rand指数(RI)
内部指标:DB指数(DBI)、Dunn指数(DI)
其中只有DB指数为越小越好
参考引用:
K-Means聚类:https://blog.csdn.net/haluoluo211/article/details/78524599
LVQ:https://blog.csdn.net/weixin_35732969/article/details/81141005
GMM:https://blog.csdn.net/FAICULTY/article/details/79343640
层次聚类:https://blog.csdn.net/sjpljr/article/details/70169222
密度聚类:https://blog.csdn.net/weixin_42134141/article/details/80413598
谱聚类:https://blog.csdn.net/xsqlx/article/details/39338989
聚类性能度量指标:https://blog.csdn.net/weixin_35732969/article/details/81137111