一、解析题目
PS:F可以为0,比如鸡蛋在 1 层都能摔碎,那么F=0。
这道题是让你找摔不碎鸡蛋的最高楼层 F,那么什么叫「最坏情况」下「至少」要扔几次呢?
「最坏情况」:假如现在先不管鸡蛋个数的限制,有 7 层楼,你怎么取找鸡蛋恰好摔碎的那层楼?最原始的方式就是线性扫描:先在 1 楼扔一下,没碎,再去 2 楼扔一下,没去,再去 3 楼……以这种策略,最坏情况应该是我试到第7层鸡蛋也没有碎,那么 F=7。这样你应该理解什么叫做「最坏情况」下了,鸡蛋破碎一定发生在搜索区间穷尽时,不会说你在第1层摔一下鸡蛋就碎了,这是你运气好,不是最坏的情况。
「至少」:假如不考虑鸡蛋个数的限制,同样是 7 层楼,我们可以优化策略:最好的策略是二分查找思路,先去 (1+7) / 2 = 4 层扔一下,如果碎了说明 F 小于 4,就去 (1 + 3) / 2 = 2层试;但如果没碎,说明 F 大于 4,就去(5 + 7)/ 2 = 6 层试…以这种策略,最坏的地方应该是试到第 7 层鸡蛋还没碎,或者鸡蛋一直碎到第 1 层还没碎。无论哪种情况,只需要试 log 7 向上取整等于 3 次,比刚才的 7 次要少,这就是所谓的至少要扔几次。
PS:这有点像 Big O 表示法计算算法的复杂度。
实际上,如果不限制鸡蛋个数的话,二分思路显然可以得到最少尝试的次数,但现在的问题是,给了鸡蛋个数的限制 K,直接用二分思路就不行了。
比如只给你 1 个鸡蛋,7 层楼,你敢用二分吗?你直接去第 4 层扔一下,如果鸡蛋没碎还好,但如果碎了你就没有鸡蛋继续测试了,无法确定鸡蛋恰好摔不碎的楼层 F 了。所以只有 1 个鸡蛋只能从第1层开始,用线性扫描的方法,一层一层往上测试,算法返回结果应该是 7 次。
有的读者也许会有这种想法:二分查找排除楼层的速度无疑是最快的,那干脆先用二分查找,等到只剩 1 个鸡蛋的时候再执行线性扫描,这样得到的结果是否就是最少的扔鸡蛋次数呢?很遗憾,并不是,比如把楼层变高一些,100层,给你 2 个鸡蛋,你在50层扔一下,碎了,那只能线性扫描1—49层了,最坏情况下要扔 50 次。但如果不要二分,变成五分、十分都会大幅减少最快情况下的尝试次数。比如第一个鸡蛋每隔10层扔,在哪里碎了第二个鸡蛋就一个个线性扫描,总共不会超过 20次。
二、思路分析
对动态规划问题,我们强调:「状态」和「选择」,然后穷举。动态规划的奥义就在穷举,消除重复子问题地穷举。
假设你有 2 个鸡蛋,4 层楼,那么一开始你面临的选择有:(第1个鸡蛋,第1层扔),(第1个鸡蛋,第2层扔),(第1个鸡蛋,第3层扔),(第1个鸡蛋,第4层扔)。为了做出这种选择,肯定有段代码是这样的:
扔鸡蛋后的状态:
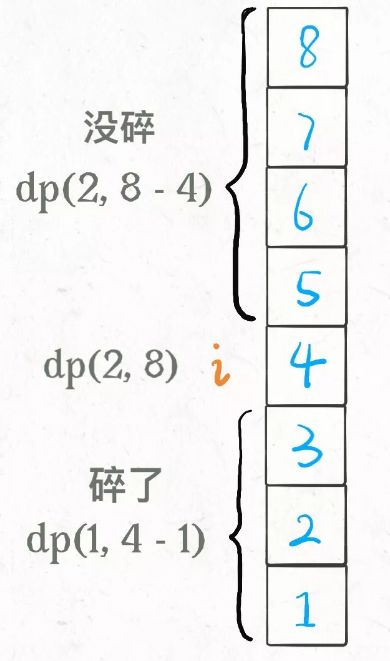
鸡蛋碎了,鸡蛋减少1,楼层范围缩小,从 [1..N] 变为 [ 1...i-1 ] 共 i-1 层楼。
鸡蛋没碎,那么鸡蛋的个数 K 不变,搜索的楼层区间应该从 [1 .. N] 变为 [ i+1 .. N ] 共 N - i 层楼。
扔完第一个鸡蛋后,要在当前状态的基础上,继续去选择在要测试的楼层上扔出第2 个鸡蛋(如果有的话)。
我们之所以无法选定每次鸡蛋在哪层楼扔出,是因为不同的方案可能需要花费不同的鸡蛋数才能确定刚好跌碎的楼层答案。我们不知道每次在哪层扔,当鸡蛋耗尽时前能够确定出楼层 F,并且消耗的鸡蛋最少。这道题其实是让我们找出一个消耗鸡蛋最小的方案,但是要在鸡蛋总数K的限制下。
所以推理到这里可以先想一想退出条件(或者一开始就应该想一想,怎样才算确定了刚好摔坏的楼层F)—— 剩下需要测试的楼层数为0,就能确定刚好摔坏的楼层。比如:第一次在2楼扔鸡蛋,恰好摔坏了,说明待检测范围收缩了,从 [1,N] 变为了[1, 1],此时还剩 1 楼没有检测,整个检测还没有结束,还需要再在 1 楼扔一次鸡蛋,坏了则说明恰好是1楼,没坏则说明恰好是 2 楼。
所以 dp 至少要维护一个状态为剩余待测楼层数 N,且有一个退出条件为 N==0;说到退出条件,那么 K == 0 时,也不能再检测了,但 K 实际上不能在确定破碎楼层之前等于0,所以退出条件应该在 K==1,当 K == 1时,剩余未检测的楼层也没有优化的机会了,只能线性全部检测一遍。所以这里维护一个结果量叫做检测次数,检测一次即+1,且若 K==1,即停止检测并直接加上剩余待检楼层数。
因为扔鸡蛋的结果可能是 【碎 or 不碎】,这是我们无法控制的,无法控制的选项,就要兼容最坏情况,即最大次数。而每次在哪层楼扔鸡蛋是我们可以选择的,所以我们可以在每次扔不同的楼层的选项组合中选出一个结果最小的作为我们的方案。
至此这道题就解决了,只要添加一个备忘录消除重叠子问题即可,最终代码如下:
动态规划算法的时间复杂度就是子问题个数 * 函数本身的复杂度。函数本身的复杂度就是忽略递归部分的复杂度,这里 dp 函数中有一个 for 训话你,所以函数本身的复杂度是 O(N)。子问题的个数也就是不同状态组合的总数,显然是两个状态的乘积 O(KN)。所以算法的总时间复杂度是 O(K*N^2)。