SG平滑轨迹算法的原理和实现
SG平滑算法是由Savizkg和Golag提出来的。基于最小二乘原理的多项式平滑算法，也称卷积平滑。为啥叫多项式平滑呢？且看下去。
下面使用五点平滑算法来说明平滑过程
原理很简单如图：
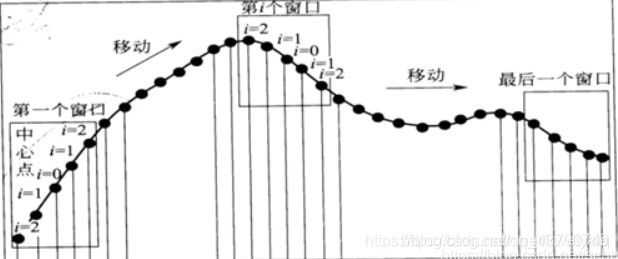假设窗口大小为5,即每次取5个点,包括自身和前后2个点
把光谱一段区间的等波长间隔的5个点记为X集合，多项式平滑就是利用在波长点为Xk−2,Xk−1,Xk,Xk+1,Xk+2的数据的多项式拟合值来取代Xk,k表示轨迹点上的第k个点,然后依次移动，直到把光谱遍历完。
Savitsky-Golay卷积平滑关键在于矩阵算子的求解。
假设滤波窗口的宽度为n = 2m+1, 各测量点x = (-m+0, -m+1, -m+2,… , m - 1, m)， 采用k-1次 多项式对窗口内的数据点进行拟合：
(1)
于是就有了n个这样的方程，组成k元线性方程组，要使方程组有解，应该满足n大于等于k，一般选择n > k。通过最小二程法拟合确定参数A。由此得到：
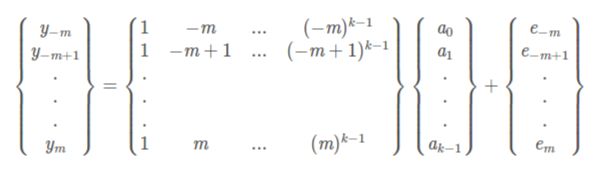
(2)
表示的是同时更新窗口呢n=2m+1个y值,但是再实现过程中,一般是窗口向前逐一移动,每次只更新中间那个点即第m个点.
使用矩阵表示：
(3)
A 的最小二乘解为：
(4)
则Y的滤波值为：
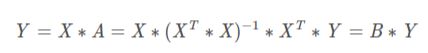
(5)
其中
(6)
再实现过程中,只更新第m个点的坐标,故在得到B矩阵后,只取B矩阵的第m行,并与窗口内的2m+1个值使用多项式拟合,从而更新窗口内的第m个点.然后窗口移动依次遍历每一个点.至于在窗口的第1个点和最后一个点,前后各缺少m个点,则使用补齐的方法,补齐方法如下:
#假设m=3,n=2*3+1=7,data = [1,2,3,4,5,6,7,8],那么对data的补齐方式如下:
mode | Ext | Input | Ext
-----------+---------+------------------------+---------
'mirror' | 4 3 2 | 1 2 3 4 5 6 7 8 | 7 6 5
'nearest' | 1 1 1 | 1 2 3 4 5 6 7 8 | 8 8 8
'constant' | 0 0 0 | 1 2 3 4 5 6 7 8 | 0 0 0
'wrap' | 6 7 8 | 1 2 3 4 5 6 7 8 | 1 2 3
(7)
实现代码如下:
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import savgol_filter
Size = 100
x = np.linspace(0,2*np.pi,100)
data = np.sin(x) + np.random.random(100) * 2
#x = np.linspace(1, Size,Size)
#data = np.random.randint(1, Size, Size)
plt.plot(x, data,color='y',label='pre_filter data')
print("input data:",data)
#savgol_filter
y = savgol_filter(data, 59, 3, mode= 'nearest')
# print(x)
plt.plot(x, y, 'b', label = 'savgol_filter')
#self
arr = []
window_size = 59
k =3
m = int((window_size-1)/2)
for i in range(window_size):#如(2),(3)
a = []
for j in range(k):
y_val = np.power(-m + i, j)
a.append(y_val)
arr.append(a)
X = np.mat(arr)#X shape:(2m+1,k)
print("变量矩阵x:",X)
#print(arr.I)
B = X * (X.T * X).I * X.T #如(6)#B shape:(2m+1,2m+1)
print("矩阵 B:",B)
# print(step)
a = np.array(B[m])#只使用矩阵的第m行,a shape:(1,2m+1)
print(a)
a = a.reshape(window_size)
print(a)
#前后补齐,如(7)
data = np.insert(data, 0, [data[0] for i in range(m)])
data = np.append(data, [data[-1] for i in range(m)])
print(data)
list = []
for i in range(m, data.shape[0] - m):
arra = []
for j in range(-m, m+1):
arra.append(data[i +j])#找到临近的window_size个点,#arra shape:(1,2m+1)
#print(arra)
b = np.sum(np.array(arra) * a)#使用多项式求解,并把多项式结果作为平滑后的点,如(1),(5)
# c = arr * (np.mat(arra).reshape(window_size,1))
# for j in range(window_size):
# data[i - step + j] = c[j][0]
# print(c.reshape(window_size))
list.append(b)#得到所有平滑后的点
print((list))
plt.plot(x, np.array(list), 'r', label = 'self')
plt.legend()
plt.savefig("sg.png",dpi=600)
plt.show()
结果如下:
可以看出我们的结果与scipy库得到的结果基本一致.