机器学习笔记27——Boosting方法之LightGBM算法原理及python实战
LightGBM算法
- 引言
- 1、LightGBM原理
-
- 1.1 Gradient-based One-Side Sampling (GOSS)算法
- 1.2 Exclusive Feature Bundling (EFB)算法
- 1.3 leaf-wise策略
- 2、LightGBM优化
-
- 2.1 带深度限制的 Leaf-wise 的叶子生长策略
- 2.2 直方图优化
- 2.3 直接支持类别特征
- 2.4 LightGBM并行优化
- 3、LightGBM优点
- 4、LightGBM代码实践
引言
\quad \quad GBDT (Gradient Boosting Decision Tree) 是机器学习中一个长盛不衰的模型,其主要思想是利用弱分类器(决策树)迭代训练以得到最优模型,该模型具有训练效果好、不易过拟合等优点。GBDT 在工业界应用广泛,通常被用于点击率预测,搜索排序等任务。虽然传统的boosting算法(如GBDT和XGBoost)已经有相当好的效率,但是在如今的大样本和高维度的环境下,传统的boosting似乎在效率和可扩展性上不能满足现在的需求了,主要的原因就是传统的boosting算法需要对每一个特征都要扫描所有的样本点来选择最好的切分点,其计算复杂度将受到特征数量和数据量双重影响,这是非常的耗时。因此,引入了LightGBM算法
1、LightGBM原理
LightGBM论文地址
\quad \quad LightGBM是个快速的、分布式的、高性能的基于决策树算法的梯度提升(GBDT算法)框架。可用于排序、分类、回归以及很多其他的机器学习任务中。
\quad \quad 为了解决这种GBDT算法在大样本高纬度数据的环境下耗时的问题,Lightgbm使用了如下几种解决办法:
1.1 Gradient-based One-Side Sampling (GOSS)算法
\quad \quad GOSS(Gradient-based One-Side Sampling, 基于梯度的单边采样),不是使用所用的样本点来计算梯度,而是对样本进行采样来计算梯度;GBDT 中每个数据都有不同的梯度值,对采样十分有用,即实例的梯度小,实例训练误差也就较小,已经被学习得很好了,直接想法就是丢掉这部分梯度小的数据。然而这样做会改变数据的分布,将会影响训练的模型的精确度,为了避免此问题,提出了 GOSS。
\quad \quad GOSS 保留所有的梯度较大的实例,在梯度小的实例上使用随机采样。为了抵消对数据分布的影响,计算信息增益的时候,GOSS 对小梯度的数据引入常量乘数。GOSS 首先根据数据的梯度绝对值排序,选取 top a 个实例。然后在剩余的数据中随机采样 b 个实例。接着计算信息增益时为采样出的小梯度数据乘以(1-a)/b,这样算法就会更关注训练不足的实例,而不会过多改变原数据集的分布。最后使用a+b个数据来计算该特征的信息增益。GOSS算法流程伪代码如下:

\quad \quad GOSS算法主要是从减少样本的角度来对GBDT进行优化的。丢弃梯度较小的样本并且在不损失太多精度的情况下提升模型训练速度,这使得LightGBM速度较快的原因之一。
1.2 Exclusive Feature Bundling (EFB)算法
\quad \quad EFB(Exclusive Feature Bundling, 互斥特征捆绑)算法,通过将两个互斥的特征捆绑在一起,合为一个特征,在不丢失特征信息的前提下,减少特征数量,从而加速模型训练。大多数时候两个特征都不是完全互斥的,可以用定义一个冲突比率对特征不互斥程度进行衡量,当冲突较小时,可以将不完全互斥的两个特征捆绑,对最后的模型型精度也没有太大影响。
\quad \quad 所谓特征互斥,即两个特征不会同时为非零值,这一点跟分类特征的one-hot表达有点类似。互斥特征捆绑算法的关键问题有两个,一个是如何判断将哪些特征进行绑定,另外一个是如何将特征进行绑定,即绑定后的特征如何进行取值的问题。
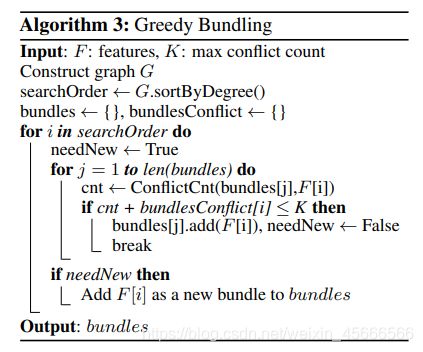
\quad \quad 针对第一个问题,EFB算法将其转化为图着色(Graph Coloring Problem)的问题来求解。其基本思路是将所有特征看作为图的各个顶点,用一条边连接不相互独立的两个特征,边的权重则表示为两个相连接的特征的冲突比例,需要绑定在一起的特征就是图着色问题中要涂上同一种眼色的点(特征)。基于图着色问题的EFB求解算法伪代码如下:
\quad \quad 第二个问题是要确定绑定后的特征如何进行取值,其关键在于能够将原始的特征从合并后的特征中进行分离,也就是说绑定到一个特征后,我们仍然可以在这个绑定的bundle里面识别出原始特征。EFB算法针对该问题尝试从直方图的角度来处理,具体做法是将不同特征值分到绑定的bundle中不同的直方图箱子中,通过在特征取值中加一个偏置常量来进行处理。举个简单的例子,假设我们要绑定特征A和特征B两个特征,特征A的取值区间为[10,20),特征B的取值区间为[10,30),我们可以给特征B的取值范围加一个偏置量10,则特征B的取值范围变成了[20,40),绑定后的特征取值范围变成了[10,40),这样特征A和特征B即可进行愉快的融合了。特征合并算法伪代码如下:
1.3 leaf-wise策略
\quad \quad 它采用最优的leaf-wise策略分裂叶子节点,然而其它的提升算法分裂树一般采用的是depth-wise或者level-wise而不是leaf-wise。因此,在LightGBM算法中,当增长到相同的叶子节点,leaf-wise算法比level-wise算法减少更多的loss。因此导致更高的精度,而其他的任何已存在的提升算法都不能够达。与此同时,它的速度也让人感到震惊,这就是该算法名字 Light 的原因。
2、LightGBM优化
LightGBM 优化部分包含以下:
-
直方图优化
- 基于 Histogram 的决策树算法
- 直方图做差加速
- 基于直方图的稀疏特征优化
-
带深度限制的 Leaf-wise 的叶子生长策略
-
直接支持类别特征(Categorical Feature)
-
Cache 命中率优化
-
多线程优化。
2.1 带深度限制的 Leaf-wise 的叶子生长策略
\quad \quad 在 Histogram 算法之上,LightGBM 进行进一步的优化。首先它抛弃了大多数 GBDT 工具使用的按层生长 (level-wise) 的决策树生长策略,而使用了带有深度限制的按叶子生长 (leaf-wise) 算法。Level-wise 过一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。但实际上 Level-wise 是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。
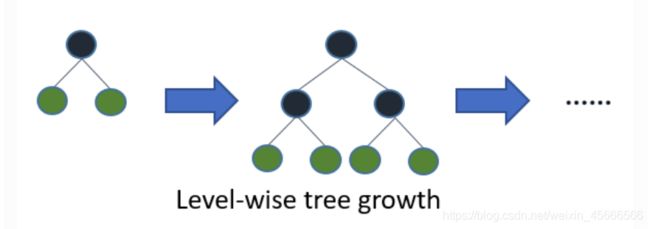
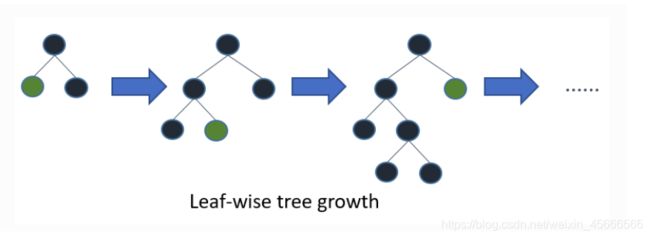
Leaf-wise 则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。因此同 Level-wise 相比,在分裂次数相同的情况下,Leaf-wise 可以降低更多的误差,得到更好的精度。Leaf-wise 的缺点是可能会长出比较深的决策树,产生过拟合。因此 LightGBM 在 Leaf-wise 之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
2.2 直方图优化
\quad \quad LightGBM 采用了直方图算法寻找最优的分割点,将连续值特征离散化,转换到不同的 bin 中,过程如下图所示:
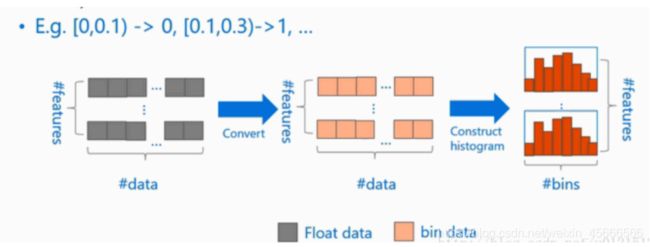
在转换到 bin 之后,还是根据和 XGBoost 一样的式子寻找最优分裂点,再回顾一下:
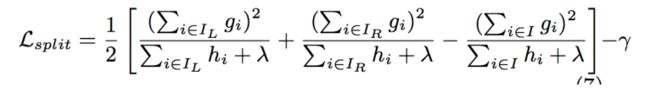
不过在分裂过程中,LightGBM 用了一个小 trick,叫做直方图做差即LightGBM 另一个优化是 Histogram(直方图)做差加速。父节点的直方图等于其左右节点的直方图的累加值,因此在实际中,统计好父节点的直方图后,我们只需要在统计数据量较少的一个子节点的直方图,数据量较大的
节点的直方图可以通过做差得到,这样又将效率提升了一倍。

综上所述,LightGBM 中用到的最优分裂点算法过程如下:
2.3 直接支持类别特征
\quad \quad 实际上大多数机器学习工具都无法直接支持类别特征,一般需要把类别特征,转化到多维的0/1 特征,降低了空间和时间的效率。而类别特征的使用是在实践中很常用的。基于这个考虑,LightGBM 优化了对类别特征的支持,可以直接输入类别特征,不需要额外的0/1 展开。并在决策树算法上增加了类别特征的决策规则。在 Expo 数据集上的实验,相比0/1 展开的方法,训练速度可以加速 8 倍,并且精度一致。
2.4 LightGBM并行优化
\quad \quad XGBoost 主要是特征粒度的并行,而 LightGBM 的并行体现在三个方面,分别是特征并行,数据并行,投票并行。但这三种并不是同时存在的,针对不同的数据集会选择不同的并行方式。
对于特征并行来说,适用于数据少,但是特征比较多的情况。LightGBM 的每个worker 保存所有的数据集,并在其特征子集上寻找最优切分点。随后,worker之间互相通信,找到全局最佳切分点。最后每个 worker 都在全局最佳切分点进行节点分裂。这样做的好处主要是减小网络通信量,但是当数据量比较大的时候,由于每个 worker 都存储的是全量数据,因此数据存储代价高。
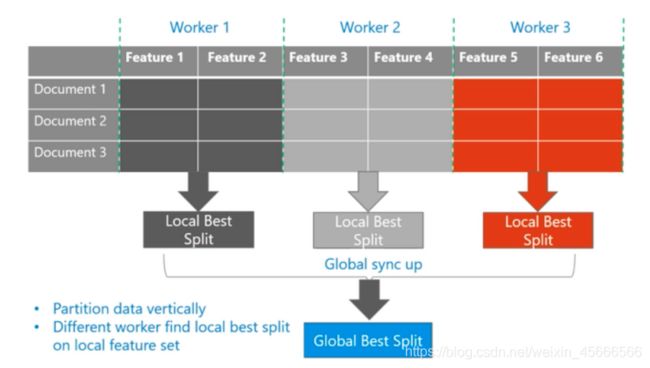
数据并行适用于数据量大,特征比较少的情况。数据并行对数据进行水平切分,每个 worker 上的数据先建立起局部的直方图,然后合并成全局的直方图,之后找到最优的分割点。

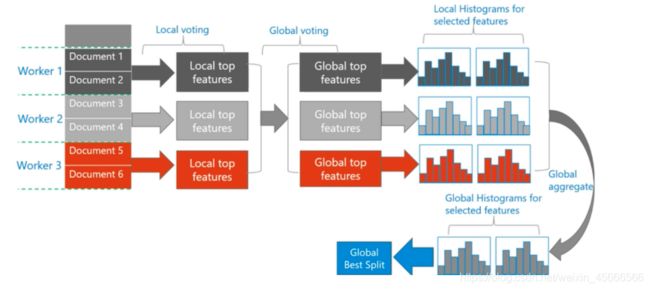
投票并行适用于数据量大,特征也比较大的情况。投票并行主要是对数据并行的一个优化。数据并行中合并直方图的时候通信代价比较大。给予投票的方式,我们只会合并部分的特征的直方图。具体来说,每个 worker 首先会找到它们数据中最优的一些特征,然后进行全局的投票,根据投票的结果,选择 top的特征的直方图进行合并,在寻求全局的最优分割点。
- 当生长相同的叶子时,Leaf-wise 比 level-wise 减少更多的损失。
- 高速,高效处理大数据,运行时需要更低的内存,支持 GPU
- 不要在少量数据上使用,会过拟合,建议 10,000+ 行记录时使用。
3、LightGBM优点
\quad \quad 相比前面提到过的系列的GB算法,LightGBM拥有如下优点:
-
速度和内存使用的优化
-
减少分割增益的计算量
-
通过直方图的相减来进行进一步的加速
-
减少内存的使用 减少并行学习的通信代价
-
-
稀疏优化
-
准确率的优化
- Leaf-wise (Best-first) 的决策树生长策略
- 类别特征值的最优分割
-
网络通信的优化
-
并行学习的优化
- 特征并行
- 数据并行
- 投票并行
-
GPU 支持可处理大规模数据
比较
4、LightGBM代码实践
\quad \quad 相关LightGBM包使用文档如下:
中文文档
英文文档
\quad \quad LightGBM提供了分类和回归两大类接口,下面以分类问题和iris数据集为例给出原生LightGBM模型的使用:
# 导入相关包
import pandas as pd
import lightgbm as lgb
from sklearn.metrics import mean_squared_error
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
# 导入数据
iris=load_iris()
data=iris.data
target=iris.target
x_train,x_test,y_train,y_test=train_test_split(data,target,test_size=0.2)
# 创建模型
gbm=lgb.LGBMRegressor(objective='regression',
num_leaves=31,
learning_rate=0.05,
n_estimators=20)
# 模型训练
gbm.fit(x_train,y_train,eval_set=[(x_test,y_test)],eval_metric='l1',early_stopping_rounds=5)
# 预测测试集
y_pred=gbm.predict(x_test,num_iteration=gbm.best_iteration_)
# 模型评估
print(mean_squared_error(y_test,y_pred)**0.5)
# 查看特征重要性
print(list(gbm.feature_importances_))
参考资料:
1、https://blog.csdn.net/weixin_43718675/article/details/102962035
2、https://blog.csdn.net/qq_22866291/article/details/99419729