神经网络及激活函数的介绍

计算机可以在眨眼间计算出复杂的数值计算。从理论上讲，它们甚至具有比人脑更大的处理能力个晶体管，对神经元的切换时间为秒，切换时间约为秒。尽管如此，大脑几乎在各个方面都胜过计算机。AI要做的是使计算机学习并基于该知识做出决策。人工智能正在使用的工具之一就是神经网络。

神经网络试图模仿大脑所具有的一些能力，这些能力是计算机不具备的。这些能力中的第一个是泛化能力。从理论上讲，计算机在任何方面都应该胜过大脑，但是计算机是静态的，无法充分发挥其潜力。另一方面，可以说，大脑是可重构的，计算机无法做到这一点。

基本上，这就是人工神经网络要完成的工作-通过复制神经系统的行为将脑功能引入计算机。

1. 神经网络背后的生物学

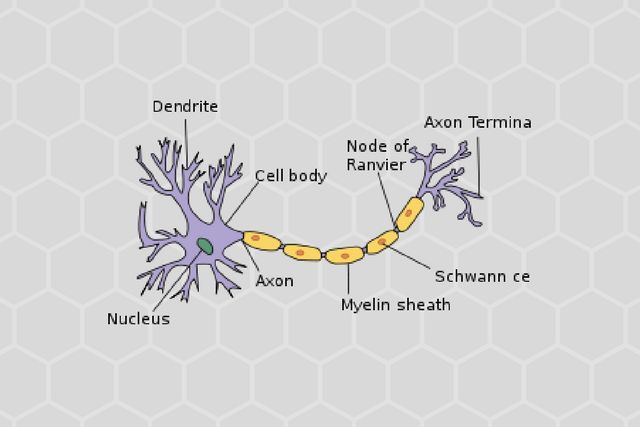
神经系统的最小单位是神经元。这些是具有相似和简单结构的单元。然而，通过持续的通信，这些单元获得了巨大的处理能力。简单地说，神经元只是开关。如果这些开关收到一定数量的输入刺激，它们就会产生输出信号。该输出信号输入到另一个神经元。

神经元是神经系统最基本的结构和功能单位。分为细胞体和突起两部分。

细胞体由细胞核、细胞膜、细胞质组成，具有联络和整合输入信息并传出信息的作用。
突起有树突和轴突两种。

树突短而分枝多，直接由细胞体扩张突出，形成树枝状，其作用是接受其他神经元轴突传来的冲动并传给细胞体。
轴突长而分枝少，为粗细均匀的细长突起，常起于轴丘，其作用是接受外来刺激，再由细胞体传出。轴突除分出侧枝外，其末端形成树枝样的神经末梢。末梢分布于某些组织器官内，形成各种神经末梢装置。感觉神经末梢形成各种感受器；运动神经末梢分布于骨骼肌肉，形成运动终极

2. 神经网络

与其他算法不同，具有深度学习功能的神经网络无法直接为任务编程。相反，就像孩子的大脑正在发育一样，他们需要学习信息。学习策略分为三种方法：

监督学习：这种学习策略是最简单的，因为有一个标记的数据集，计算机会经过该数据集，并且对该算法进行修改，直到可以处理该数据集以获得所需的结果为止。
无监督学习：在没有可用于学习的标记数据集的情况下使用此策略。神经网络分析数据集，然后代价函数告诉神经网络距目标有多远。然后，神经网络进行调整以提高算法的准确性。
强化学习：在该算法中，对神经网络进行了强化以获得正面结果，而对惩罚进行了负面评估，从而迫使神经网络随着时间的推移而学习。

2.1 神经网络的基础

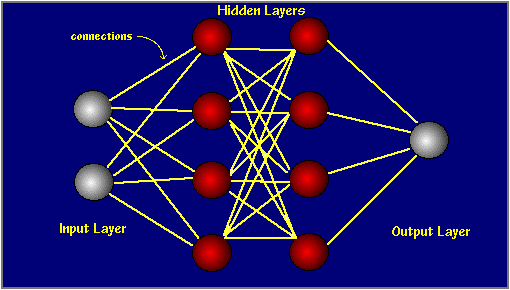
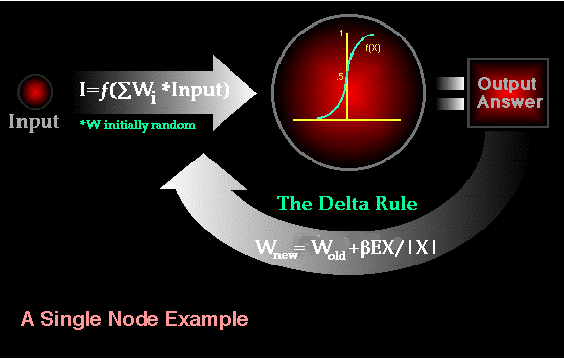
神经网络通常是分层组织的。层由多个互连的“节点”组成，这些节点包含“激活功能”。模式通过“输入层”呈现给网络，该“输入层”与一个或多个“隐藏层”进行通信，其中实际处理是通过加权“连接”系统完成的。然后，隐藏层链接到“输出层”，在该输出层输出答案，如下图所示。

神经网络原理图

反向传播（BPNN）“学习”是一个监督过程，它通过输出的前向激活流在每个周期（即，每次向网络提供新的输入模式时）发生，以及权重调整的向后误差传播。更简单地说，当最初为神经网络提供某种模式时，它会随机猜测其可能是什么。然后，它查看其答案与实际答案有多远，并对其连接权重进行适当调整。更形象地讲，该过程如下所示：

反向传播的单节点示例

BNN-RoadMap

还要注意，每个隐藏层节点中都有一个S型激活函数，它使网络活动变化并帮助其稳定。

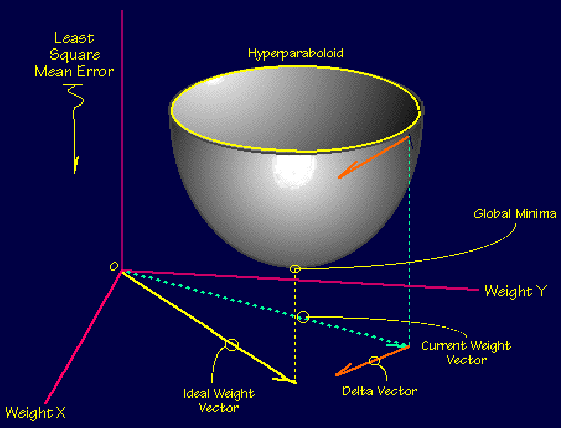
反向传播在解决方案的向量空间内沿着误差表面的最陡向量向着“全局最小值”执行梯度下降。全局最小值可能是具有最小误差的理论解。误差表面本身是双曲面，但很少有“平滑”现象，如下图所示。确实，在大多数问题中，解决方案空间是非常不规则的，有许多“坑”和“山”，这可能导致网络陷入“局部最小值”，而这并不是最佳的整体解决方案。

反向传播如何找到正确的答案

由于先验错误空间的性质是未知的，因此神经网络分析通常需要大量的单独运行才能确定最佳解决方案。大多数学习规则都具有内置的数学术语来辅助此过程，从而控制学习的“速度”和“动量”。学习速度实际上是当前解决方案与全局最小值之间的收敛速度。动量可帮助网络克服错误表面中的障碍（局部最小值）并在全局最小值处或附近沉降下来。

一旦将神经网络“训练”到令人满意的水平，就可以将其用作其他数据的分析工具。为此，用户不再指定任何训练运行，而是仅允许网络以正向传播模式工作。新的输入呈现给输入模式，在其中它们像经过训练一样被过滤并由中间层进行处理，但是，此时输出被保留并且没有反向传播发生。前向传播运行的输出是数据的预测模型，然后可以将其用于进一步的分析和解释。

过度训练神经网络也是可能的，这意味着该网络已被精确训练为仅对一种类型的输入做出响应；这很像死记硬背。如果发生这种情况，则学习将不再发生，并且在神经网络术语中将网络称为“祖母”。在实际应用中，这种情况不是很有用，因为对于每种新的输入，都需要一个单独的祖母网络。

2.2 神经网络的局限性

神经网络分析有很多优点和局限性，要正确讨论该主题，我们必须查看每种单独的网络类型，这对于一般性的讨论不是必需的。但是，对于反向传播网络，潜在用户应注意一些特定问题。

在某种意义上，反向传播神经网络（以及许多其他类型的网络）是最终的“黑匣子”。除了定义网络的总体架构，并可能最初使用随机数为网络播种之外，用户没有其他作用，除了馈送网络输入并观看网络训练并等待输出。实际上，已经有人说过反向传播，“您几乎不知道自己在做什么”。某些软件免费提供的软件包（NevProp，bp，Mactivation）确实允许用户以固定的时间间隔对网络“进行”采样，但学习本身会自行进行。
反向传播网络的训练也往往比其他类型的网络慢。如果在真正的并行计算机系统上运行，则此问题并不是真正的问题，但是，如果在标准串行计算机（即单个SPARC，Mac或PC）上模拟BPNN，则培训可能会花费一些时间。这是因为机器CPU必须分别计算每个节点和连接的功能，这在具有大量数据的超大型网络中可能会出现问题。

2.3 相比传统技术相比的优势？

根据应用程序的性质和内部数据模式的强度，通常可以期望网络训练得很好。这适用于关系可能非常动态或非线性的问题。人工神经网络为常规技术提供了一种分析替代方法，而传统技术通常受到严格的正态性，线性，变量独立性等假设的限制。由于人工神经网络可以捕获多种关系，因此它使用户可以快速而轻松地对现象进行建模。

3. 激活函数

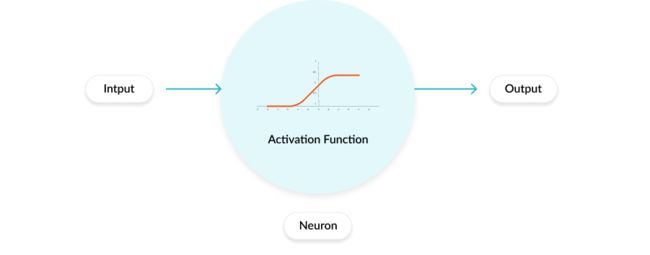
激活函数是确定神经网络输出的数学方程式。该功能附加到网络中的每个神经元，并根据每个神经元的输入是否与模型的预测相关来确定是否应激活（“触发”）该功能。激活功能还有助于将每个神经元的输出标准化为1到0或-1到1之间的范围。

激活函数的另一个方面是，它们必须具有高效的计算能力，因为对于每个数据样本而言，它们是在数千乃至数百万个神经元中计算得出的。现代神经网络使用一种称为反向传播的技术来训练模型，该模型在激活函数及其导数函数上增加了计算压力

3.1 激活函数在神经网络模型中的作用

在神经网络中，称为输入的数字数据点被馈送到输入层的神经元中。每个神经元都有一个权重，将输入数字乘以权重就可以得到神经元的输出，该输出将传输到下一层。

激活函数是馈送当前神经元的输入与其进入下一层的输出之间的数学“门”。它可以像根据规则或阈值打开和关闭神经元输出的阶跃函数一样简单。也可以是将输入信号映射为神经网络起作用所需的输出信号的转换。

神经网络越来越多地使用非线性激活函数，它可以帮助网络学习复杂数据，计算和学习几乎代表问题的任何函数，并提供准确的预测。

神经网络中神经元执行的基本过程

3.2 三种激活函数类型

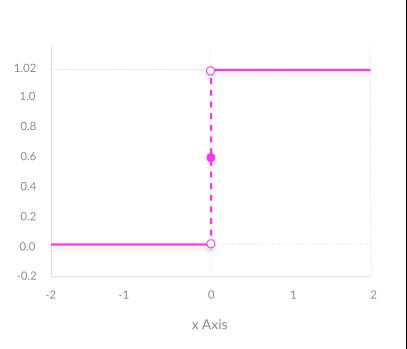
二进制步进函数(Binary Step Function)

二进制步进函数是基于阈值的激活函数。如果输入值高于或低于某个阈值，则神经元被激活并将完全相同的信号发送到下一层。

神经网络中的二阶步激活函数

步进功能的问题在于它不允许多值输出，例如，它不支持将输入分类为几种类别之一。

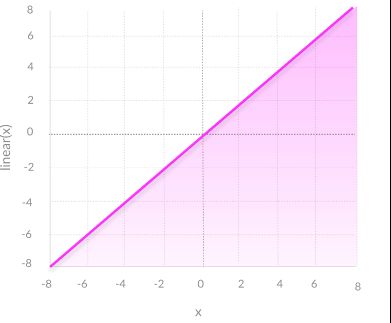
线性激活函数

线性激活函数的形式为：

A = cx

神经网络中的线性激活函数

它获取输入，然后乘以每个神经元的权重，然后创建与输入成比例的输出信号。从某种意义上说，线性函数优于步进函数，因为它允许多个输出，而不仅仅是yes和no。

但是，线性激活函数有两个主要问题：

1.不能使用反向传播（梯度下降）来训练模型-函数的导数是常数，并且与输入X无关。因此，无法返回并了解输入神经元中的权重可以提供更好的预测。

2.神经网络的所有层都折叠为一个具有线性激活函数，无论神经网络中有多少层，最后一层都是第一层的线性函数（因为线性函数的线性组合仍然是线性函数）。因此，线性激活函数将神经网络变成一层。

具有线性激活函数的神经网络就是线性回归模型。它具有有限的能力和能力来处理输入数据的复杂度变化的参数。

非线性激活函数

现代的神经网络模型使用非线性激活函数。它们使模型可以在网络的输入和输出之间创建复杂的映射，这对于学习和建模复杂的数据（例如图像，视频，音频和非线性或高维数据集）至关重要。

只要激活函数是非线性的，几乎可以想象的任何过程都可以表示为神经网络中的函数计算。

非线性函数解决了线性激活函数的问题：

它们允许反向传播，因为它们具有与输入有关的微分函数。
它们允许“堆叠”多层神经元来创建一个深层的神经网络。需要多个隐藏的神经元层，以高精度地学习复杂的数据集。

3.3 非线性激活函数

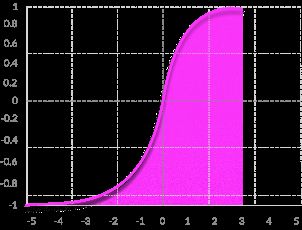
Sigmoid / Logistic

sigmoid函数也叫Logistic函数，用于隐层神经元输出，取值范围为(0,1)，它可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid作为激活函数有以下优缺点：

优点

平滑梯度，易于求导，防止输出值“跳跃”。

输出值介于0和1之间，对每个神经元的输出进行标准化。

清晰的预测 -对于X大于2或低于-2的X，趋向于将Y值（预测）带到曲线的边缘，非常接近1或0。这可以实现清晰的预测。

缺点

梯度消失 –对于非常高或非常低的X值，预测几乎没有变化，从而导致梯度消失问题。这可能导致网络拒绝进一步学习，或者太慢而无法获得准确的预测。

输出中心不是零。

计算代价大

TanH / Hyperbolic Tangent

$\begin{aligned} \tanh ^{\prime}(x) &=\left(\left(e^{x}-e^{-x}\right)\left(e^{x}+e^{-x}\right)^{-1}\right)^{\prime} \\ &=\left(e^{x}+e^{-x}\right)\left(e^{x}+e^{-x}\right)^{-1}-\left(e^{x}-e^{-x}\right)\left(e^{x}+e^{-x}\right)^{-2}\left(e^{x}-e^{-x}\right) \\ &=1-\frac{\left(e^{x}-e^{-x}\right)^{2}}{\left(e^{x}+e^{-x}\right)^{2}} \\ &=1-\tanh ^{2}(x) \end{aligned}$
是双曲函数中的一个，为双曲正切。在数学中，双曲正切“tanh”是由基本双曲函数双曲正弦和双曲余弦推导而来。

函数：；定义域：，值域：。是一个奇函数，其函数图像为过原点并且穿越Ⅰ、Ⅲ象限的严格单调递增曲线，其图像被限制在两水平渐近线和之间。

优点

以零为中心-使具有强负，中性和强正值的输入更容易建模。否则就像Sigmoid函数。

缺点

像Sigmoid函数

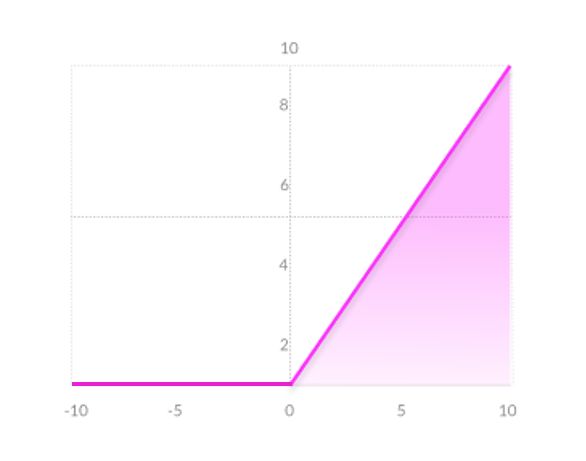
ReLU (Rectified Linear Unit)

线性整流函数（Rectified Linear Unit, ReLU），又称修正线性单元，是一种人工神经网络中常用的激活函数（activation function），通常指代以斜坡函数及其变种为代表的非线性函数。

通常意义下，线性整流函数指代数学中的斜坡函数，即

而在神经网络中，线性整流作为神经元的激活函数，定义了该神经元在线性变换之后的非线性输出结果。换言之，对于进入神经元的来自上一层神经网络的输入向量，使用线性整流激活函数的神经元会输出

至下一层神经元或作为整个神经网络的输出（取决现神经元在网络结构中所处位置）

相比于传统的神经网络激活函数，诸如逻辑函数（Logistic sigmoid）和tanh等双曲函数，线性整流函数有着以下几方面的优势：

优点

计算效率高-允许网络快速收敛

非线性-尽管ReLU看起来像线性函数，但它具有导数函数并允许反向传播

仿生物学原理：相关大脑方面的研究表明生物神经元的信息编码通常是比较分散及稀疏的。通常情况下，大脑中在同一时间大概只有1%-4%的神经元处于活跃状态。使用线性修正以及正则化（regularization）可以对机器神经网络中神经元的活跃度（即输出为正值）进行调试；相比之下，逻辑函数在输入为0时达到，即已经是半饱和的稳定状态，不够符合实际生物学对模拟神经网络的期望。不过需要指出的是，一般情况下，在一个使用修正线性单元（即线性整流）的神经网络中大概有50%的神经元处于激活态。

更加有效率的梯度下降以及反向传播：避免了梯度爆炸和梯度消失问题

简化计算过程：没有了其他复杂激活函数中诸如指数函数的影响；同时活跃度的分散性使得神经网络整体计算成本下降。

缺点

静止ReLU问题 —当输入接近零或为负时，函数的梯度变为零，网络无法执行反向传播，也无法学习。

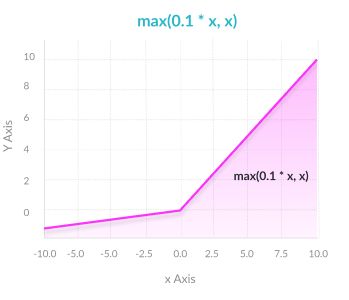
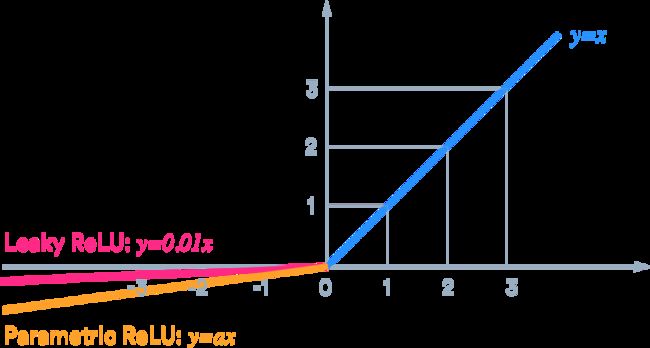
Leaky ReLU

数学表达式：y = max(0, x) + leak*min(0,x) （leak是一个很小的常数，这样保留了一些负轴的值，使得负轴的信息不会全部丢失）

优点

防止静止ReLU问题 -ReLU的这种变化在负区域具有小的正斜率，因此即使对于负输入值，它也确实可以进行反向传播，否则像ReLU

缺点

结果不一致-Leaky ReLU无法为负输入值提供一致的预测。

Parametric ReLU

如果，那么PReLU退化为ReLU；如果是一个很小的固定值(如)，则PReLU退化为Leaky ReLU(LReLU)。有实验证明，与ReLU相比，LReLU对最终的结果几乎没什么影响

优点

允许学习负斜率-与Leaky ReLU不同，此函数提供函数负数部分的斜率作为参数。因此，可以进行反向传播并学习最合适的α值，否则像ReLU。

缺点

对于不同的问题可能会有所不同。

PReLU的几点说明

（1） PReLU只增加了极少量的参数，也就意味着网络的计算量以及过拟合的危险性都只增加了一点点。特别的，当不同channels使用相同的时，参数就更少了。

（2） BP更新时，采用的是带动量的更新方式，如下公式：

上式的两个系数分别是动量和学习率。
需要特别注意的是：更新时不施加权重衰减(L2正则化)，因为这会把很大程度上push到0。事实上，即使不加正则化，试验中ai也很少有超过1的

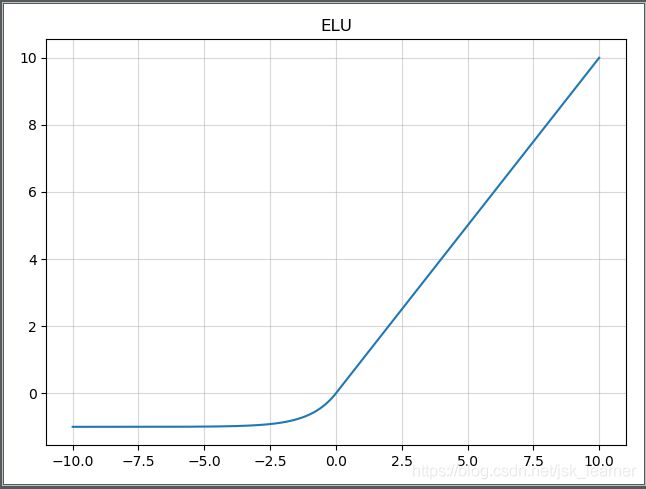
ELU

$\begin{array}{l} f(x)=\left\{\begin{array}{ll} \alpha\left(e^{x}-1\right), & x \leq 0 \\ x, & x>0 \end{array}\right. \\ f^{\prime}(x)=\left\{\begin{array}{ll} f(x)+\alpha, & x \leq 0 \\ 1, & x>0 \end{array}\right. \end{array}$

指数线性单元(exponential linear unit)，该激活函数由Djork等人提出,被证实有较高的噪声鲁棒性,同时能够使得使得神经元的平均激活均值趋近为 0,同时对噪声更具有鲁棒性。由于需要计算指数,计算量较大。

SELU

image.png

SELU是给ELU乘上系数, 即

这个是大于1的，以前relu，prelu，elu这些激活函数，都是在负半轴坡度平缓，这样在activation的方差过大的时候可以让它减小，防止了梯度爆炸，但是正半轴坡度简单的设成了1。而selu的正半轴大于1，在方差过小的的时候可以让它增大，同时防止了梯度消失。这样激活函数就有一个不动点，网络深了以后每一层的输出都是均值为0方差为1。

Softmax

归一化指数函数，或Softmax函数，实际上是有限项离散概率分布的梯度对数归一化。是逻辑函数的一种推广。它能将一个含任意实数的K维向量z“压缩”到另一个K维实向量σ(z)中，使得每一个元素的范围都在(0,1)之间，并且所有元素的和为1。该函数多于多分类问题中。

优点

能够处理其他激活函数中的一个类别的多个类别 -将每个类别的输出归一化在0和1之间，并除以它们的总和，从而得出输入值属于特定类别的可能性。

对于输出神经元很有用-Softmax通常仅用于输出层，用于需要将输入分类为多个类别的神经网络。

Swish

β是个常数或可训练的参数.Swish 具备无上界有下界、平滑、非单调的特性。

Swish是Google研究人员发现的一种新的自门激活功能。根据这篇论文，它的性能优于ReLU。

在具有运行ReLU和Swish的相同模型的ImageNet上进行的实验中，新功能将top -1分类精度提高了0.6-0.9％。

当β = 0时,Swish变为线性函数 ,
为0或1. Swish变为ReLU: f(x)=2max(0,x)
所以Swish函数可以看做是介于线性函数与ReLU函数之间的平滑函数.

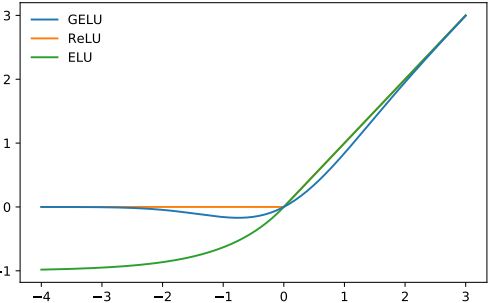
GELU(Gaussian Error Linerar Units)

在神经网络的建模过程中，模型很重要的性质就是非线性，同时为了模型泛化能力，需要加入随机正则，例如dropout(随机置一些输出为0,其实也是一种变相的随机非线性激活)，而随机正则与非线性激活是分开的两个事情，而其实模型的输入是由非线性激活与随机正则两者共同决定的。

GELUs正是在激活中引入了随机正则的思想，是一种对神经元输入的概率描述，直观上更符合自然的认识，同时实验效果要比Relus与ELUs都要好。

GELUs其实是 dropout、zoneout、Relus的综合，GELUs对于输入乘以一个0,1组成的mask，而该mask的生成则是依概率随机的依赖于输入。假设输入为X, mask为m，则m服从一个伯努利分布, 这么选择是因为神经元的输入趋向于正太分布，这么设定使得当输入x减小的时候，输入会有一个更高的概率被dropout掉，这样的激活变换就会随机依赖于输入了。

数学表达如下：

这里是正太分布的概率函数，可以简单采用正太分布, 要是觉得不刺激当然可以使用参数化的正太分布, 然后通过训练得到。

对于假设为标准正太分布的GELU(x), 论文中提供了近似计算的数学公式，如下：

GELU (μ=0, σ=1), ReLU and ELU (α=1)

GELU vs Swish

GELU 与 Swish 激活函数（x · σ(βx)）的函数形式和性质非常相像，一个是固定系数 1.702，另一个是可变系数 β（可以是可训练的参数，也可以是通过搜索来确定的常数），两者的实际应用表现也相差不大。

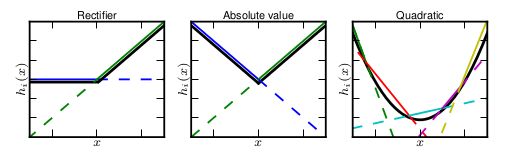
Maxout

Maxout可以看做是在深度学习网络中加入一层激活函数层,包含一个参数k.这一层相比ReLU,sigmoid等,其特殊之处在于增加了k个神经元,然后输出激活值最大的值.

我们常见的隐含层节点输出：

而在Maxout网络中，其隐含层节点的输出表达式为：

其中

以如下最简单的多层感知器(MLP)为例:

假设网络第i层有2个神经元x1、x2，第i+1层的神经元个数为1个.原本只有一层参数,将ReLU或sigmoid等激活函数替换掉,引入Maxout,将变成两层参数,参数个数增为k倍.

优点：

Maxout的拟合能力非常强，可以拟合任意的凸函数。

Maxout具有ReLU的所有优点，线性、不饱和性。

同时没有ReLU的一些缺点。如：神经元的死亡。

缺点：

从上面的激活函数公式中可以看出，每个神经元中有两组(w,b)参数，那么参数量就增加了一倍，这就导致了整体参数的数量激增。

与常规激活函数不同的是,它是一个可学习的分段线性函数.

然而任何一个凸函数，都可以由线性分段函数进行逼近近似。其实我们可以把以前所学到的激活函数：ReLU、abs激活函数，看成是分成两段的线性函数，如下示意图所示：

实验结果表明Maxout与Dropout组合使用可以发挥比较好的效果。

那么,前边的两种ReLU便是两种Maxout,函数图像为两条直线的拼接,

4. 激活函数的导数或梯度

激活函数的导数（也称为梯度）对于训练神经网络非常重要。

使用称为反向传播的过程来训练神经网络，这是一种算法，该算法从模型的输出追溯到生成该输出所涉及的不同神经元，再追溯到应用于每个神经元的原始权重。反向传播建议每个神经元的最佳权重，这将导致最准确的预测。

梯度爆炸
由于sigmoid,ReLU等函数的梯度都在[0,1]以内，所以不会引发梯度爆炸问题。而梯度爆炸需要采用梯度裁剪、BN、设置较小学习率等方式解决。

5. 激活函数选择

首先尝试ReLU,速度快,但要注意训练的状态.
如果ReLU效果欠佳,尝试Leaky ReLU或Maxout等变种。
尝试tanh正切函数(以零点为中心,零点处梯度为1)
sigmoid/tanh在RNN（LSTM、注意力机制等）结构中有所应用，作为门控或者概率值.
在浅层神经网络中，如不超过4层的，可选择使用多种激励函数，没有太大的影响。

结论

神经网络是一个有趣且不断发展的话题。而且，这些网络具有广泛的应用范围。当前，它们主要用于预测，分类和自动化，但是我们会发现越来越多的应用程序。至于破坏人类和道德价值贬低，那还是基于人类如何定义去发展，我们作为人类本身是希望它能够给我带来的辅助科技发展、社会进步。我们不可对它过于吹捧，同时需要对它有一种重视的态度，因为在未知的事物面前我们可能使想的远了，也有可能我们目前看的还远远不够。

参考

Introduction to Artificial Neural Networks

What is a neural network?

A Basic Introduction To Neural Networks

7 Types of Neural Network Activation Functions: How to Choose?

Sigmoid, Softmax and their derivatives

Sigmoid函数百度百科

双曲正切_百度百科

ReLU函数百度百科

激活函数Relu 及 leakyRelu

ReLU与PReLU

归一化指数函数百度百科

ReLU、LReLU、PReLU、CReLU、ELU、SELU

激活函数(ReLU, Swish, Maxout)

Gaussian Error Linerar Units(GELUS)