算法提高之搜索:BFS中的双向广搜和A-star
目录
- 1、双向广搜
-
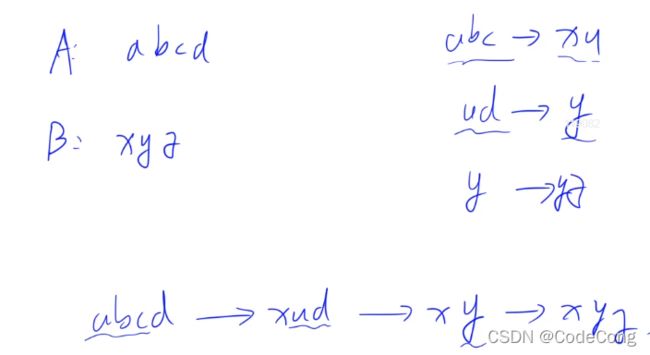
- 1.1、字串变换
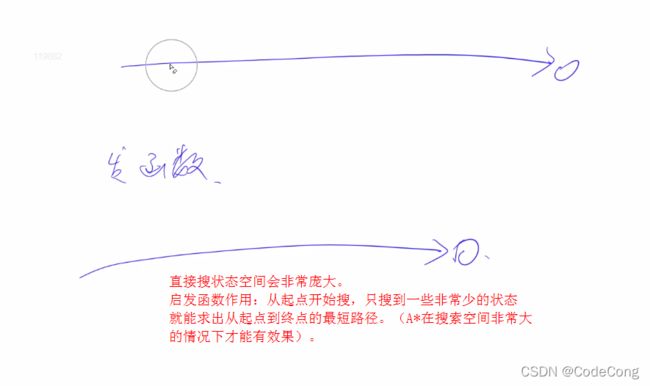
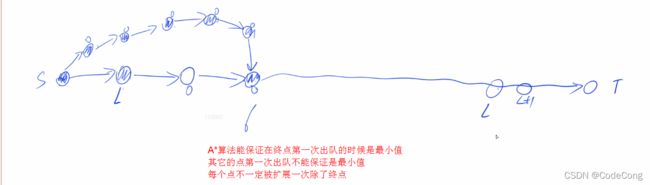
- 2、A-star
-
- 2.1、第k短路
- 2.2、八数码
1、双向广搜
1.1、字串变换
#include 2、A-star
2.1、第k短路
#include 2.2、八数码


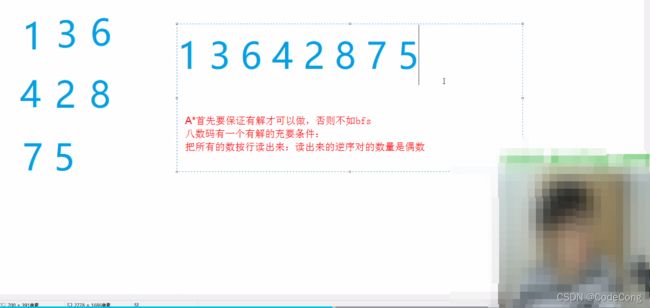
估价函数的取法:是保证当前状态的估计距离小于等于当前状态到终点的真实距离。原因是每个点不可能直接按照曼哈顿距离移动到他想去的位置。需要迂回一下才能到。因此估价函数取曼哈顿距离一定小于真实距离。

#include